An example to dive in to: matrix factorization and recommendation systems
Return to A Moment of Science: LLVM An example to dive in to: matrix factorization and recommendation systems Matrix factorization methods serve as the backbone of many statist…

Return to A Moment of Science: LLVM
An example to dive in to: matrix factorization and recommendation systems
Matrix factorization methods serve as the backbone of many statistical algorithms. Two particular approaches -- singular value decomposition (SVD) and non-negative matrix factorization -- gained broader exposure with the 2009 Netflix Prize for improving movie recommendations. These are both computationally expensive algorithms, the kind that you want implemented in a compiled language. But, there is a nice tutorial on using matrix factorization for recommendation systems that codes the algorithm in Python, making the algorithm easy to follow and test. I'll be using a slightly modified version of the code used in this tutorial as the basis for my explorations.
Mathematically, what we are doing is taking an N by M matrix R of ratings by N people over M items and decomposing it into two constituent matrices, P and Q (I'll stick with the notation used in the tutorial). P will be an N by K matrix that we can think of as N people's preference weightings over K "hidden" (or latent) features of the items. Q will be a K by M matrix that we can think of as the "loadings" on the K features by each of these M items. The algorithm seeks P and Q such that the difference between R and PQ is minimized (in general, this solution is non-unique).
In what follows I'll compare algorithm speed across three scenarios:
- Python
- C
- Python on the LLVM using numba
Baseline code
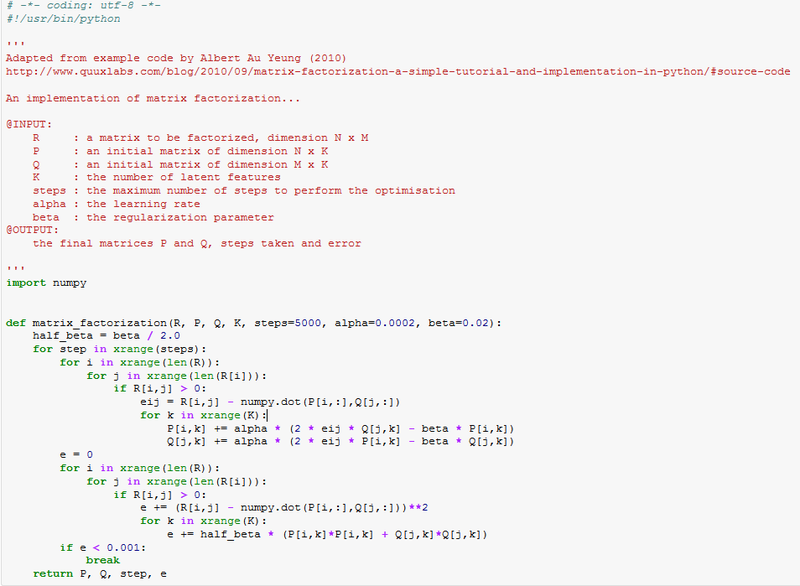
Here is the code that will serve as the baseline for our testing (again, a slightly modified version of what is hosted on the tutorial). We'll save this code as a file called mf.py
Right away, we can see this will probably run very slowly in a language like Python compared to C. We have deeply nested for loops and such looping is almost always a bottleneck in dynamically typed languages (relative to doing the exact same looping in a compiled language in which the compiler knows about the variable types and can optimize operations).
In two parts of the code there is an important conditional statement to call out with respect to how the algorithm is adapted to this rating recommendation problem:
if R[i,j] > 0:
In the R matrix of peoples' ratings on items, R[i,j] = 0 is a sentinel meaning that person i has not rated item j. In many settings (like Netflix's inventory of thousands of movies), most elements of R will be 0 because most people have only interacted with a small subset of the items. The algorithm above takes this into account when assessing the factorization error by ignoring the differences between the estimated R and the actual R where the actual ratings are unknown. In this way, the algorithm tries to find P and Q such that the known ratings are recovered as accurately as possible. Estimates for the unobserved ratings, i.e., the predicted ratings, can then be taken from PQ wherever R was zero. We assume that ratings are non-negative, e.g. 1-5 stars.
One final thing deserves mention before we run the code: we have to pick K, the number of latent features. But if the features are latent, how do we know how many of them there are? There is no easy answer in most settings. Some amount of experimentation and domain expertise (to interpret the factors) is needed to confidently pick K, but this touches on an important issue that pervades statistical modeling: estimation error due to model selection is often harder to assess and correct than error due to model fitting, but much more is written about the latter. For this example we'll use 8 factors.
Performance testing
OK, finally we are on to testing performance. In support of this testing I am going to define two variants of the baseline code, and finally a piece of code to easily call all three variants.
The first variant we'll save to a file called mf_cython.pyx. We'll take advantage of a Cython, which essentially lets us add some type information to our Python code above and then machine-generate analogous C code that be compiled and execute (much) more quickly. I won't post this code here but will link to it an the end.
The second variant we'll save to a file called mf_numba.py and will use numba to add type information and generate "intermediate" code that can be JIT compiled by LLVM. One of the nice things about numba is that you can do this through a simple function decorator. For example, instead of our matrix_factorization method beginning as
def matrix_factorization(R, P, Q, K):
we import autojit from numba and then add this decorator. It auto-majically annotates the variables types in the code and prepares it for JIT compilation:
from numba.decorators import autojit
@autojit
def matrix_factorization(R, P, Q, K):
At this point, we have our baseline Python implementation of matrix factorization for recommendation problems, along with two variants that use C and LLVM for improving execution speed. Finally, we need a bit of code to drive the test, which I have in a file called mf_rec_test.py. This code creates some random ratings data for a desired number of people and items. The run method then calls one of the three matrix factorization variants we have and measures execution time along with the error in recovering the known ratings. Again, I won't post the code here but will link to it at the end.
With everything in place we can drive the test across the three approaches an compare speed. Again, 8 factors will be used in the solution, and we'll pick a relatively small matrix of 30 people having ratings over 60 items...
In [1]: import mf_rec_test as mfrt
In [2]: mfrt.run(method='python', num_factors=8, num_users=30, num_items=60)
Recommendation test time in minutes: 2.9021
Factorization RMSE: 0.087
In [3]: mfrt.run(method='cython', num_factors=8, num_users=30, num_items=60)
Recommendation test time in minutes: 0.0028
Factorization RMSE: 0.081
So, the Python code takes almost 3 minutes whereas the (machine-generated) C code executes in one thousandth of the time. For languages like Python and R much of the mathematical and statistical methods are actually calling underlying C and Fortran code, so you can get reasonably good execution speed to go along with the development productivity you get. But, as this example shows, there are cases where highly iterative algorithms can suffer horribly. How does the numba-ized code fair?
In [4]: mfrt.run(method='numba', num_factors=8, num_users=30, num_items=60)
Recommendation test time in minutes: 0.0652
Factorization RMSE: 0.088
Pretty impressive: for code that we basically added a one-line decorator to, we sped things up by a factor of 44. Now, watch what happens if we re-execute the exact same call:
In [5]: mfrt.run(method='numba', num_factors=8, num_users=30, num_items=60)
Recommendation test time in minutes: 0.0031
Factorization RMSE: 0.084
The numba-ized code now executes in the same time as the C code, speeding up again by a factor of 21. How so? The first time the numba-ized code is run it gets translated to byte code that LLVM can JIT compile. The next time we run the code, the results from the JIT compilation can be used and we get another big speed up.
Return to A Moment of Science: LLVM
Popular Posts

Business and IT Alignment is Critical to Your AI Success
These are the five pillars that can unite business and IT goals and convert artificial intelligence into measurable value — fast
Read more
FICO® Score 10T Decisively Beats VantageScore 4.0 on Predictability
An analysis by FICO data scientists has found that FICO Score 10T significantly outperforms VantageScore 4.0 in mortgage origination predictive power.
Read more
Average U.S. FICO Score at 717 as More Consumers Face Financial Headwinds
Outlier or Start of a New Credit Score Trend?
Read moreTake the next step
Connect with FICO for answers to all your product and solution questions. Interested in becoming a business partner? Contact us to learn more. We look forward to hearing from you.