Introduction
Mathematical Programming
Mathematical Programming is a technique of mathematical optimization. Many real-world problems in such different areas as industrial production, transport, telecommunications, finance, or personnel planning may be cast into the form of a Mathematical Programming problem: a set of decision variables, constraints over these variables and an objective function to be maximized or minimized.
Mathematical Programming problems are usually classified according to the types of the decision variables, constraints, and the objective function.
A well-understood case for which efficient algorithms (Simplex, interior point) are known comprises Linear Programming (LP) problems. In this type of problem all constraints and the objective function are linear expressions of the decision variables, and the variables have continuous domains—i.e., they can take on any, usually non-negative, real values. Luckily, many application problems fit into this category. Problems with hundreds of thousands, or even millions of variables and constraints are routinely solved with commercial Mathematical Programming software like Xpress Optimizer.
Researchers and practitioners working on LP quickly found that continuous variables are insufficient to represent decisions of a discrete nature (`yes'/`no' or 1,2,3,...). This observation lead to the development of Mixed Integer Programming (MIP) where constraints and objective function are linear just as in LP and variables may have either discrete or continuous domains. To solve this type of problems, LP techniques are coupled with an enumeration (known as Branch-and-Bound) of the feasible values of the discrete variables. Such enumerative methods may lead to a computational explosion, even for relatively small problem instances, so that it is not always realistic to solve MIP problems to optimality. However, in recent years, continuously increasing computer speed and even more importantly, significant algorithmic improvements (e.g. cutting plane techniques and specialized branching schemes) have made it possible to tackle ever larger problems, modeling ever more exactly the underlying real-world situations.
Another class of problems that is relatively well-handled are Quadratic Programming (QP) problems: these differ from LPs in that they have quadratic terms in the objective function (the constraints remain linear). The decision variables may be continuous or discrete, in the latter case we speak of Mixed Integer Quadratic Programming (MIQP) problems. In Chapters 7 and 12 of this book we show examples of both cases.
More difficult is the case of non-linear constraints or objective functions, Non-linear Programming (NLP) problems. Frequently heuristic or approximation methods are employed to find good (locally optimal) solutions. One method for solving problems of this type is Successive Linear Programming (SLP); such a solver forms part of the FICO Xpress Optimization suite. However, in this book we shall not enlarge on this topic.
Building a model, solving it and then implementing the `answers' is not generally a linear process. We often make mistakes in our modeling which are usually only detected by the optimization process, where we could get answers that were patently wrong (e.g. unbounded or infeasible) or that do not accord with our intuition. If this happens we are forced to reflect further about the model and go into an iterative process of model refinement, re-solution and further analyses of the optimum solution. During this process it is quite likely that we will add extra constraints, perhaps remove constraints that we were mislead into adding, correct erroneous data or even be forced to collect new data that we had previously not considered necessary.
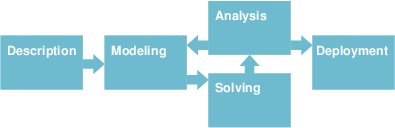
Figure 2.1: Scheme of an optimization project
This books takes the reader through all these steps: from the textual description we develop a mathematical model which is then implemented and solved. Various improvements, additions and reformulations are suggested in the following chapters, including an introduction of the available means to support the analysis of the results. The deployment of a Mathematical Programming application typically includes its embedding into other applications to turn it into a part of a company's information system.
Xpress product suite
Arising from different users' needs and preferences, there are several ways of working with the modeling and optimization tools that form the FICO Xpress Optimization product suite:
- High-level language: the Xpress Mosel language allows the user to define his models in a form that is close to algebraic notation and to solve them in the same environment. Mosel's programming facilities also make it possible to implement solution algorithms directly in this high-level language. Mosel may be used as a standalone program or through the Xpress Workbench development environment that provides, amongst many other tools, Mosel syntax and debugging support.
Via the concept of modules the Mosel environment is entirely open to additions; modules of the Xpress distribution include access to solvers (Xpress Optimizer for LP, MIP, and convex QP, Xpress Nonlinear, and Xpress Kalis), data handling facilities (e.g. via ODBC), access to system functions, graphing capabilities, distributed and remote computing functionality via the Mosel Distributed Framework, and also interfaces to statistics packages such as R or Matlab. In addition, via the Mosel Native Interface users may define their own modules to add new features to the Mosel language according to their needs (e.g. to implement problem-specific data handling, or connections to external solvers or solution algorithms). - Deployment as a web app: Mosel models can be deployed via Xpress Insight as multi-user web apps running locally, on-premises or on a cloud. Insight web apps are configured via a set of XML files that are packaged into an archive along with the Mosel model and its input data.
- Libraries for embedding: two different options are available for embedding mathematical models into host applications. A model developed using the Mosel language may be executed and accessed from a programming language environment (e.g. C, C++, Java, etc.) through the Mosel libraries; certain modules also provide direct access to their functions from a programming language environment.
The second possibility consists of developing a model directly in a programming language with the help of the model builder library Xpress-BCL. BCL allows the user to formulate his models with objects (decision variables, constraints, index sets) similar to those of a dedicated modeling language.
All libraries are available for C, C++, Java, C#, and Visual Basic (VBA). - Direct access to solvers: on the lowest, most immediate level, it is possible to work directly with the Xpress Optimizer or Xpress NonLinear in the form of a library or a standalone program. This facility may be useful for embedding Xpress Optimizer into applications that possess their own, dedicated matrix generation routines.
Advanced Xpress users may wish to employ special features of Xpress Optimizer that are not available through the different interfaces, possibly using a matrix that has previously been generated by Mosel or BCL.
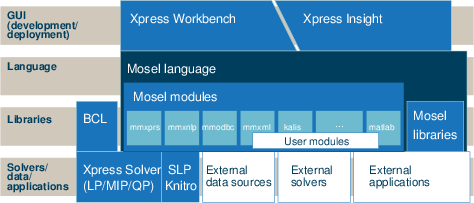
Figure 2.2: Xpress product suite
Of the three above mentioned approaches, a high-level language certainly provides the easiest-to-understand access to Mathematical Programming. So in the first and largest part of this book we show how to define and solve problems with the Xpress Mosel language, and also how the resulting models may be embedded into applications using the Mosel libraries or Xpress Insight. We work with Mosel models in the graphical user interface Xpress Workbench, exploiting its facilities for debugging and solution analysis and display.
In the reminder of this book we show how to formulate and solve Mathematical Programming problems directly in a programming language environment. This may be done with modeling support from BCL or directly using the Optimizer library. With BCL, models can be implemented in a form that is relatively close to their algebraic formulation and so are quite easy to understand and to maintain. We discuss BCL implementations of the same example problems as used with Mosel.
The last part of this book explains how problems may be input directly into Xpress Optimizer, either in the form of matrices (possibly generated by another tool such as Mosel or BCL) that are read from file, or by specifying the problem matrix coefficient-wise directly in the application program. The facility of working directly with the Xpress Optimizer library is destinated at embedders and advanced Xpress users. It is not recommendable as a starting point for the novice in Mathematical Programming.
Note on product versions
The Mosel examples in this book have been updated to the FICO Xpress Optimization Release 8.3 (Mosel 4.6.0); Xpress Workbench screenshots have been taken with Release 8.3 (Workbench version 2.0.0). The Xpress Insight examples have been developed with Xpress Release 8.3 (Insight 4.8). The BCL examples are using BCL 4.8.11 that is distributed with Xpress Release 8.3. The Xpress Optimizer examples have equally been updated to the Xpress Release 8.3 (Optimizer 31.01.09). If the examples are run with other product versions the output obtained may look different. In particular, improvements to the algorithms or modifications to the default settings in the Optimizer may influence the behavior of the LP search or the shape of the MIP branching trees. The Xpress Workbench interface may also undergo slight changes in future releases as new features are added, but this will not affect the actions described in this book.

