MIP formulations using other entities
In principle, all you need in building MIP models are continuous variables and binary variables. But it is convenient to extend the set of modeling entities to embrace objects that frequently occur in practice.
- values 0, 1, 2, ... up to small upper bound
- model discrete quantities
- try to use partial integer variables instead of integer variables with a very large upper bound
- may be zero, or any value between the intermediate bound and the upper bound
- Semi-continuous integer variables also available: may be zero, or any integer value between the intermediate bound and the upper bound
- set of decision variables
- each variable has a different ordering value, which orders the set
- Special ordered sets of type 1 (SOS1): at most one variable may be non-zero
- Special ordered sets of type 2 (SOS2): at most two variables may be non-zero; the non-zero variables must be adjacent in ordering
Batch sizes
Must deliver in batches of 10, 20, 30, ...
- Decision variables
nship number of batches delivered: integer ship quantity delivered: continuous - Constraint formulation
ship = 10 · nship
Ordered alternatives
Suppose you have N possible investments of which at most one can be selected. The capital cost is CAPi and the expected return is RETi.
- Often use binary variables to choose between alternatives. However, SOS1 are more efficient to choose between a set of graded (ordered) alternatives.
- Define a variable di to represent the decision, di = 1 if investment i is picked
- Binary variable (standard) formulation
di : binary variablesMaximize: ret = ∑i RETidi ∑i di ≤ 1 ∑i CAPidi ≤ MAXCAP - SOS1 formulation
{di; ordering value CAPi} : SOS1Maximize: ret = ∑i RETidi ∑i di ≤ 1 ∑i CAPidi ≤ MAXCAP - Special ordered sets in Mosel
- special ordered sets are a special type of linear constraint
- the set includes all variables in the constraint
- the coefficient of a variable is used as the ordering value (i.e., each value must be unique)
declarations I=1..4 d: array(I) of mpvar CAP: array(I) of real My_Set, Ref_row: linctr end-declarations My_Set:= sum(i in I) CAP(i)*d(i) is_sos1
or alternatively (must be used if a coefficient is 0):Ref_row:= sum(i in I) CAP(i)*d(i) makesos1(My_Set, union(i in I) {d(i)}, Ref_row)
- Special ordered sets in BCL
- a special ordered set is an object of type XPRBsos
- the set includes all variables from the specified linear expression or constraint that have a coefficient different from 0
- the coefficient of a variable is used as the ordering value (i.e., each value must be unique)
XPRBprob prob("testsos"); XPRBvar d[I]; XPRBexpr le; XPRBsos My_Set; double CAP[I]; int i; for(i=0; i<I; i++) d[i] = prob.newVar("d"); for(i=0; i<I; i++) le += CAP[i]*d[i]; My_Set = prob.newSos("My_Set", XPRB_S1, le);
Price breaks
All items discount: when buying a certain number of items we get discounts on all items that we buy if the quantity we buy lies in certain price bands.
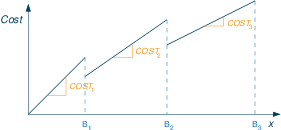
| less than B1 | COST1 each |
| ≥ B1 and < B2 | COST2 each |
| ≥ B2 and < B3 | COST3 each |
- Define binary variables bi (i=1,2,3), where bi is 1 if we pay a unit cost of COSTi.
- Real decision variables xi represent the number of items bought at price COSTi.
- The quantity bought is given by x= ∑ixi , with a total price of ∑iCOSTi·xi
- MIP formulation :
where the variables bi are either defined as binaries, or they form a Special Ordered Set of type 1 (SOS1), where the order is given by the values of the breakpoints Bi.∑i bi = 1 x1 ≤ B1· b1 Bi-1· bi ≤ xi ≤ Bi· bi for i=2,3
Incremental pricebreaks: when buying a certain number of items we get discounts incrementally. The unit cost for items between 0 and B1 is C1, items between B1 and B2 cost C2 each, etc.
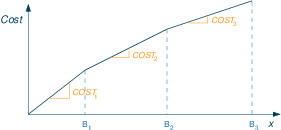
Formulation with Special Ordered Sets of type 2 (SOS2):
- Associate real valued decision variables wi (i=0,1,2,3) with the quantity break points B0 = 0, B1, B2 and B3.
- Cost break points CBPi (=total cost of buying quantity Bi):
CBP0=0 CBPi = CBPi-1+Ci· (Bi-Bi-1) for i=1,2,3 - Constraint formulation:
where the wi form a SOS2 with reference row coefficients given by the coefficients in the definition of the total amount x.∑iwi=1 TotalCost = ∑i CBPi· wi x = ∑i Bi· wi
For a solution to be valid, at most two of the wi can be non-zero, and if there are two non-zero they must be contiguous, thus defining one of the line segments. - Implementation with Mosel (is_sos2 cannot be used here due to the 0-valued coefficient of w0):
Defx := x = sum(i in 1..3) B(i)*w(i) makesos2(My_Set, union(i in 0..3) {w(i)}, Defx)
Formulation using binaries:
- Define binary variables bi (i=1,2,3), where bi is 1 if we have bought any items at a unit cost of COSTi.
- Real decision variables xi (i=1,..3) for the number of items bought at price COSTi.
- Total amount bought: x = ∑i xi
- Constraint formulation:
(Bi-Bi-1)\cdot bi+1 ≤ xi ≤ (Bi-Bi-1)\cdot bi for i=1,2 x3 ≤ (B3-B2)\cdot b3 b1 ≥ b2 ≥ b3
Non-linear functions
Can model non-linear functions in the same way as incremental pricebreaks
- approximate the non-linear function with a piecewise linear function
- use an SOS2 to model the piecewise linear function
Non-linear function in a single variable
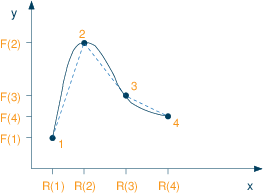
- x-coordinates of the points: R1, ..., R4
y-coordinates F1, ..., F4. So point 1 is (R1,F1) etc. - Let weights (decision variables) associated with point i be wi (i=1,...,4)
- Form convex combinations of the points using weights wi to get a combination point (x,y):
where the variables wi form an SOS2 set with ordering coefficients defined by values Ri.x = ∑i wi·Ri y = ∑i wi·Fi ∑i wi = 1 - Mosel implementation:
declarations I=1..4 x,y: mpvar w: array(I) of mpvar R,F: array(I) of real end-declarations ! ...assign values to arrays R and F... ! Define the SOS-2 with "reference row" coefficients from R Defx:= sum(i in I) R(i)*w(i) is_sos2 sum(i in I) w(i) = 1 ! The variable and the corresponding function value we want to approximate x = Defx y = sum(i in I) F(i)*w(i)
- BCL implementation:
XPRBprob prob("testsos"); XPRBvar x, y, w[I]; XPRBexpr Defx, le, ly; double R[I], F[I]; int i; // ...assign values to arrays R and F... // Create the decision variables x = prob.newVar("x"); y = prob.newVar("y"); for(i=0; i<I; i++) w[i] = prob.newVar("w"); // Define the SOS-2 with "reference row" coefficients from R for(i=0; i<I; i++) Defx += R[i]*w[i]; prob.newSos("Defx", XPRB_S2, Defx); for(i=0; i<I; i++) le += w[i]; prob.newCtr("One", le == 1); // The variable and the corresponding function value we want to approximate prob.newCtr("Eqx", x == Defx); for(i=0; i<I; i++) ly += F[i]*w[i]; prob.newCtr("Eqy", y == ly);
Non-linear function in two variables
Interpolation of a function f in two variables: approximate f at a point P by the corners C of the enclosing square of a rectangular grid (NB: the representation of P=(x,y) by the four points C obviously means a fair amount of degeneracy).
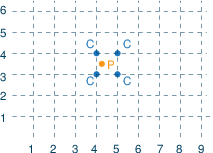
- x-coordinates of grid points: X1, ..., Xn
y-coordinates of grid points: Y1, ..., Ym. So grid points are (Xi,Yj). - Function evaluation at grid points: FXY11, ..., FXYnm
- Define weights (decision variables) associated with x and y coordinates, wxi respectively wyj, and for each grid point (X(i),Y(j)) define a variable wxyij
- Form convex combinations of the points using the weights to get a combination point (x,y) and the corresponding function approximation:
where the variables wxi form an SOS2 set with ordering coefficients defined by values Xi, and the variables wyj are a second SOS2 set with coordinate values Yj as ordering coefficients.x = ∑i wxi·Xi y = ∑j wyj·Yj f = ∑ij wxyij·FXYij ∀ i=1,...,n: ∑j wxyij = wxi ∀ j=1,...,m: ∑i wxyij = wyj ∑i wxi = 1 ∑j wyj = 1 - Mosel implementation:
declarations RX,RY:range X: array(RX) of real ! x coordinate values of grid points Y: array(RY) of real ! y coordinate values of grid points FXY: array(RX,RY) of real ! Function evaluation at grid points end-declarations ! ... initialize data declarations wx: array(RX) of mpvar ! Weight on x coordinate wy: array(RY) of mpvar ! Weight on y coordinate wxy: array(RX,RY) of mpvar ! Weight on (x,y) coordinates x,y,f: mpvar end-declarations ! Definition of SOS (assuming coordinate values <>0) sum(i in RX) X(i)*wx(i) is_sos2 sum(j in RY) Y(j)*wy(j) is_sos2 ! Constraints forall(i in RX) sum(j in RY) wxy(i,j) = wx(i) forall(j in RY) sum(i in RX) wxy(i,j) = wy(j) sum(i in RX) wx(i) = 1 sum(j in RY) wy(j) = 1 ! Then x, y and f can be calculated using x = sum(i in RX) X(i)*wx(i) y = sum(j in RY) Y(j)*wy(j) f = sum(i in RX,j in RY) FXY(i,j)*wxy(i,j) ! f can take negative or positive values (unbounded variable) f is_free
XPRBprob prob("testsos"); XPRBvar x, y, f; XPRBvar wx[NX], wy[NY], wxy[NX][NY]; // Weights on coordinates XPRBexpr Defx, Defy, le, lexy, lx, ly; double DX[NX], DY[NY]; double FXY[NX][NY]; int i,j; // ... initialize data arrays DX, DY, FXY // Create the decision variables x = prob.newVar("x"); y = prob.newVar("y"); f = prob.newVar("f", XPRB_PL, -XPRB_INFINITY, XPRB_INFINITY); // Unbounded variable for(i=0; i<NX; i++) wx[i] = prob.newVar("wx"); for(j=0; j<NY; j++) wy[j] = prob.newVar("wy"); for(i=0; i<NX; i++) for(j=0; j<NY; j++) wxy[i][j] = prob.newVar("wxy"); // Definition of SOS for(i=0; i<NX; i++) Defx += X[i]*wx[i]; prob.newSos("Defx", XPRB_S2, Defx); for(j=0; j<NY; j++) Defy += Y[j]*wy[j]; prob.newSos("Defy", XPRB_S2, Defy); // Constraints for(i=0; i<NX; i++) { le = 0; for(j=0; j<NY; j++) le += wxy[i][j]; prob.newCtr("Sumx", le == wx[i]); } for(j=0; j<NY; j++) { le = 0; for(i=0; i<NX; i++) le += wxy[i][j]; prob.newCtr("Sumy", le == wy[j]); } for(i=0; i<NX; i++) lx += wx[i]; prob.newCtr("Convx", lx == 1); for(j=0; j<NY; j++) ly += wy[j]; prob.newCtr("Convy", ly == 1); // Calculate x, y and the corresponding function value f we want to approximate prob.newCtr("Eqx", x == Defx); prob.newCtr("Eqy", y == Defy); for(i=0; i<NX; i++) for(j=0; j<NY; j++) lexy += FXY[i][j]*wxy[i][j]; prob.newCtr("Eqy", f == lexy);
Minimum activity level
Continuous production rate make. May be 0 (the plant is not operating) or between allowed production limits MAKEMIN and MAKEMAX
- Can impose using a semi-continuous variable: may be zero, or any value between the intermediate bound and the upper bound
- Mosel:
make is_semcont MAKEMIN
make <= MAKEMAX
make = prob.newVar("make", XPRB_SC, 0, MAKEMAX);
make.setLim(MAKEMIN);
Partial integer variables
- In general, try to keep the upper bound on integer variables as small as possible. This reduces the number of possible integer values, and so reduces the time to solve the problem.
- Sometimes this is not possible – a variable has a large upper bound and must take integer values.
⇒ Try to use partial integer variables instead of integer variables with a very large upper bound: takes integer values for small values, where it is important to be precise, but takes real values for larger values, where it is OK to round the value afterwards. - For example, it may be important to clarify whether the value is 0, 1, 2, ..., 10, but above 10 it is OK to get a real value and round it.
- Mosel:
x is_partint 10 ! x is integer valued from 0 to 10 x <= 20 ! x takes real values from 10 to 20
x = prob.newVar("x", XPRB_PI, 0, 20); x.setLim(10);

