split_domain
split_domain |
Purpose
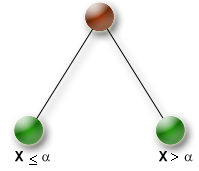
Creates a split_domain branching scheme. This will split the domain of every branching variable X in two parts, one branch with the case X ≤ alpha and the other branch X > alpha where alpha is a value in the domain of X.

Synopsis
function split_domain(varsel:string, valsel:string, variables:set of cpvar, leqfirst:boolean, stopsplit: integer) : cpbranching
function split_domain(varsel:string, valsel:string, variables:array(range) of cpvar, leqfirst:boolean, stopsplit: integer) : cpbranching
function split_domain(varsel:string, valsel:string, variables:cpvarlist, leqfirst:boolean, stopsplit: integer) : cpbranching
function split_domain(varsel:string, valsel:string, leqfirst:boolean, stopsplit: integer) : cpbranching
function split_domain(varsel:string, valsel:string) : cpbranching
function split_domain(varsel:string, valsel:string, variables:array(range) of cpvar, leqfirst:boolean, stopsplit: integer, probeLevel:integer) : cpbranching
function split_domain(varsel:string, valsel:string, variables:set of cpfloatvar, leqfirst:boolean, stopsplit: integer) : cpbranching
function split_domain(varsel:string, valsel:string, variables:array(range) of cpfloatvar, leqfirst:boolean, stopsplit: integer) : cpbranching
Arguments
|
varsel
|
the variable selector name (pre-defined constant or user-defined function name)
|
|
valsel
|
the value selector (pre-defined constant or user-defined function name)
|
|
variables
|
list of variables to branch on
|
|
leqfirst
|
Explore the case ≤ first if
true
|
|
stopsplit
|
stop branching if the size of the domain of the variable is less than stopsplit
|
Return value
split_domain branching scheme
Example
The following example shows how to use a split_domain branching scheme during the search
model "User branching"
uses "kalis"
parameters
ALG=1
end-parameters
forward function varchoice(Vars: cpvarlist): integer
forward function varchoice2(Vars: cpvarlist): integer
forward function valchoice(x: cpvar): integer
forward function valchoice2(x: cpvar): integer
setparam("KALIS_DEFAULT_LB", 0);
setparam("KALIS_DEFAULT_UB", 20)
declarations
R = 1..10
y: array(R) of cpvar
C: array(R) of integer
Strategy: array(range) of cpbranching
end-declarations
C:: [4, 7, 2, 6, 9, 0,-1, 3, 8,-2]
all_different(y)
forall(i in R | isodd(i)) y(i) >= y(i+1) + 1
y(4) + y(1) = 13; y(8) <= 15; y(7) <> 5
! Definition of user branching strategies:
Strategy(1):= assign_and_forbid("varchoice2", "valchoice", y)
Strategy(2):= assign_var("varchoice", "valchoice", y)
Strategy(3):= split_domain("varchoice", "valchoice2", y, true, 2)
Strategy(4):= split_domain("varchoice2", "valchoice", y, false, 5)
! Select a branching strategy
cp_set_branching(Strategy(ALG))
if cp_find_next_sol then
forall(i in R) write(getsol(y(i)), " ")
writeln
end-if
!---------------------------------------------------------------
! **** Variable choice ****
! **** Choose variable with largest degree + smallest domain
function varchoice(Vars: cpvarlist): integer
declarations
Vset,Iset: set of integer
end-declarations
! Get the number of elements of "Vars"
listsize:= getsize(Vars)
! Set on uninstantiated variables
forall(i in 1..listsize)
if not is_fixed(getvar(Vars,i)) then Vset+= {i}; end-if
if Vset={} then
returned:= 0
else
! Get the variables with max. degree
dmax:= max(i in Vset) getdegree(getvar(Vars,i))
forall(i in Vset)
if getdegree(getvar(Vars,i)) = dmax then Iset+= {i}; end-if
dsize:= MAX_INT
! Choose var. with smallest domain among those indexed by 'Iset'
forall(i in Iset)
if getsize(getvar(Vars,i)) < dsize then
returned:= i
dsize:= getsize(getvar(Vars,i))
end-if
end-if
writeln(returned)
end-function
! **** Choose variable y(i) with smallest value of C(i)
function varchoice2(Vars: cpvarlist): integer
declarations
Vset,Iset: set of integer
VarInd: array(Iset) of integer
end-declarations
! Set on uninstantiated variables
listsize:= getsize(Vars)
forall(i in 1..listsize)
if not is_fixed(getvar(Vars,i)) then Vset+= {i}; end-if
if getsize(Vset)=0 then
returned:= 0
else
! Establish a correspondence of indices between 'Vars' and 'y'
forall(i in R)
forall(j in Vset)
if is_same(getvar(Vars,j), y(i)) then
VarInd(i):= j
Vset -= {j}
break 1
end-if
! Choose the variable
imin:= min(i in Iset) i; cmin:= C(imin)
forall(i in Iset)
if C(i) < cmin then
imin:= i; cmin:= C(i)
end-if
returned:= VarInd(imin)
end-if
writeln(imin, " ", returned)
end-function
!---------------------------------------------------------------
! *** Value choice ****
! **** Choose the next value one third larger than lower bound
! (Strategy may be used with any branching scheme since it
! makes sure that the chosen value lies in the domain)
function valchoice(x: cpvar): integer
! returned:= getlb(x)
returned:= getnext(x, getlb(x) + round((getub(x)-getlb(x))/3))
writeln("Value: ", returned, " ", contains(x,returned),
" x: ", x)
end-function
! **** Split the domain into lower third and upper two thirds
! (Strategy to be used only with 'split_domain' branching since
! the chosen value may not be in the domain)
function valchoice2(x: cpvar): integer
returned:= getlb(x) + round((getub(x)-getlb(x))/3)
writeln("Value: ", returned, " x: ", x)
end-function
end-model
Related topics

