Using the Java Mosel interface
Overview
The Java Mosel interface offers a more advanced control and interaction with Mosel than what is possible with the simple moselexec function. In fact, the Java Mosel interface enables the user to:
- compile source model files into binary model (bim) files
- load and unload bim files handling several models at a time
- execute models
- access the Mosel internal database through the Post Processing Interface
- manage the dynamic shared objects used by Mosel
We will show some of these functionalities in the following examples, however please refer to:
- the "Xpress Mosel User Guide", Chapter 14, for a brief introduction to the Java interface;
- the "Xpress Mosel Library Reference Manual" in JavaDoc format, for the full reference documentation of this interface;
- MATLAB Documentation - Advanced Software Development - Call Java Libraries, for details on using Java from MATLAB.
Furthermore, the I/O driver described in the previous section can also be used in this context.
Compiling and executing a model
With Java, Mosel is initialized by creating a new instance of class XPRM. In MATLAB you can either use the fully qualified class name (including the package name) as in
>> mosel=com.dashoptimization.XPRM;
or import the package and then use class names without the package name:
>> import com.dashoptimization.*; >> mosel=XPRM;
The standard compile/load/run sequence becomes
>> mosel=com.dashoptimization.XPRM;
>> mosel.compile('burglar2.mos');
>> mod=mosel.loadModel('burglar2.bim');
>> mod.run;
>> mod.getResult; If the model execution is embedded in a larger application it may be useful to release the resources allocated by a model after its execution. This can be done through standard finalization + garbage collection functionalities, by calling the finalize method on the model:
>> mod.finalize
The mosel object can be released in the same way (mosel.finalize).
Accessing arrays
In general, Mosel entities such as scalar variables, sets, etc. can be queried through the findIdentifier method and retrieved in the same way as described in the "Xpress Mosel User Guide". However, when calling Java from MATLAB, it is not possible to pass an array of a Java native type to a function and receive back in MATLAB the array as modified by the function. This would be the case, for instance, when using the nextIndex or nextTEindex methods on a Mosel array. Consider the following example that defines a (sparse) array VALUE with two indices of type string:
model example_m6
declarations
CITIES = {"london", "paris", "madrid", "rome", "florence"}
ZONES = {"north", "south", "east", "west"}
VALUE: dynamic array(CITIES,ZONES) of real
end-declarations
VALUE("london", "east") := 1
VALUE("rome", "west") := 2
VALUE("paris", "south") := 3
VALUE("madrid", "east") := 4
end-model The array VALUE can be retrieved into MATLAB with the following code (example_m6.m):
value = mod.findIdentifier('VALUE');
value_iter = value.indices(true);
sets = value.getIndexSets();
while value_iter.hasNext
indices = value_iter.next;
fprintf(1, 'VALUE ( ');
for i=1:size(indices,1)
fprintf(1, '%s ', char(sets(i).get(indices(i))));
end
fprintf(1, ') = %g\n', value.getAsReal(indices));
end Executing this script would print the Mosel array as shown below:
>> example_m6 VALUE ( london east ) = 1 VALUE ( madrid east ) = 4 VALUE ( paris south ) = 3 VALUE ( rome west ) = 2
In the above example we use the iterator value_iter to loop over all valued elements of the array; at each iteration we retrieve the actual numerical indices (indices) of the current element, their corresponding values (sets(i).get(...)), and the value of the current element (value.getAsReal(indices)).
Please note that the following alternative approach that uses XPRMArray.nextTEIndex(), would not work correctly in MATLAB as the call to value.nextTEIndex(indices) cannot update the indices array as in pure Java.
indices=value.getFirstTEIndex; ... while value.nextTEIndex(indices) ... end
Examples
The first example, ugsol.m is a variation of the program ugsol.java described in the "Xpress Mosel User Guide". Here the Mosel program has been embedded in a MATLAB script: the model is the same but problem data is read from MATLAB variables and the solution is exported to MATLAB. The MATLAB script compiles the Mosel program, runs it, checks the solution status and prints the solution.
mos={
'model Burglar_m '
' uses "mmxprs" '
' declarations '
' WTMAX = 102 ! Maximum weight allowed '
' ITEMS: range '
' VALUE: array(ITEMS) of real ! Value of items '
' WEIGHT: array(ITEMS) of real ! Weight of items '
' take: array(ITEMS) of mpvar ! 1 if we take item i; 0 otherwise '
' end-declarations '
' '
' initializations from "matlab.mws:" '
' VALUE '
' WEIGHT '
' end-initializations '
' '
' MaxVal:= sum(i in ITEMS) VALUE(i)*take(i) ! Objective: max total value'
' sum(i in ITEMS) WEIGHT(i)*take(i) <= WTMAX ! Weight restriction '
' forall(i in ITEMS) take(i) is_binary ! All variables are 0/1 '
' maximize(MaxVal) ! Solve the MIP-problem '
' '
' initializations to "matlab.mws:" '
' evaluation of array(i in ITEMS) take(i).sol as "TAKE" '
' end-initializations '
'end-model '
};
ITEMS ={'camera' 'necklace' 'vase' 'picture' 'tv' 'video' 'chest' 'brick'};
VALUE =[ 15 100 90 60 40 15 10 1];
WEIGHT=[ 2 20 20 30 40 30 60 10];
mosel=com.dashoptimization.XPRM; % Initialize Mosel
mosel.compile('', 'matlab.mws:mos', 'burglar_m.bim');
mod=mosel.loadModel('burglar_m.bim');
mod.run;
if mod.getProblemStatus~=mod.PB_OPTIMAL, return, end
fprintf(1,'Objective value: %g\n', mod.getObjectiveValue); % show objective
table(ITEMS',logical(TAKE),VALUE','VariableNames',{'Item' 'Take' 'Value'})
fprintf(1,'Calculated objective: %g\n', VALUE*TAKE); % verify sol
mod.finalize The second example is a variation of the portfolio optimization from the Getting Started with Xpress guide. The Mosel program, foliomat2.mos, is almost identical to the foliodat.mos example, modified only to use integer indices instead of string indices, and to read input from MATLAB and write results to MATLAB.
model "Portfolio optimization with LP"
uses "mmxprs" ! Use Xpress Optimizer
parameters
DATAFILE= "matlab.mws:" ! File with problem data
MAXRISK = 1/3 ! Max. investment into high-risk values
MAXVAL = 0.3 ! Max. investment per share
MINAM = 0.5 ! Min. investment into N.-American values
end-parameters
writeln("Solving for MAXRISK: ", MAXRISK)
declarations
SHARES: range ! Set of shares
NAMES: array(SHARES) of string ! Names of the shares
RISK: set of integer ! Set of high-risk values among shares
NA: set of integer ! Set of shares issued in N.-America
RET: array(SHARES) of real ! Estimated return in investment
end-declarations
initializations from DATAFILE
NAMES RISK RET NA
end-initializations
declarations
frac: array(SHARES) of mpvar ! Fraction of capital used per share
end-declarations
! Objective: total return
Return:= sum(s in SHARES) RET(s)*frac(s)
! Limit the percentage of high-risk values
sum(s in RISK) frac(s) <= MAXRISK
! Minimum amount of North-American values
sum(s in NA) frac(s) >= MINAM
! Spend all the capital
sum(s in SHARES) frac(s) = 1
! Upper bounds on the investment per share
forall(s in SHARES) frac(s) <= MAXVAL
! Solve the problem
maximize(Return)
! Solution printing to a file
writeln("Total return: ", getobjval)
forall(s in SHARES)
writeln(strfmt(NAMES(s),-12), ": \t", strfmt(getsol(frac(s))*100,5,2), "%")
initializations to "matlab.mws:"
evaluation of getobjval as "objval"
evaluation of getprobstat=XPRS_OPT as "optsol"
evaluation of array(s in SHARES) frac(s).sol as "frac"
end-initializations
end-model The following MATLAB script (foliomat2.m) first initializes input data (also deriving integer indices from strings for variables RISK and NA), it then executes the Mosel program for different values of MAXRISK, from 0.1 to 0.9 at 0.1 steps, and finally displays a couple of result tables and charts of share utilization for the different risks.
NAMES ={'treasury' 'hardware' 'theater' 'telecom' 'brewery' 'highways' 'cars' 'bank'
'software' 'electronics'};
RET =[ 5 17 26 12 8 9 7 6 31 21 ];
DEV =[ 0.1 19 28 22 4 3.5 5 0.5 25 16 ];
COUNTRY={'Canada' 'USA' 'USA' 'USA' 'UK' 'France' 'Germany' 'Luxemburg' 'India' 'Japan'};
RISK_N ={'hardware' 'theater' 'telecom' 'software' 'electronics'};
NA_N ={'treasury' 'hardware' 'theater' 'telecom'};
RISK=cellfun(@(n) strmatch(n,NAMES,'exact'), RISK_N); % find indices of high-risk shares
NA =cellfun(@(n) strmatch(n,NAMES,'exact'), NA_N); % find indices of N.-American shares
for m=1:9
moselexec('foliomat2.mos',['MAXRISK=' num2str(m/10)]);
obj(m)=objval;
optimal(m)=optsol;
fracm(m,:)=frac;
end
disp('Results');
disp('Estimated returns:');
disp(table([1:9]'/10,obj','VariableNames',{'MaxRisk' 'Return'}))
disp('Average share utilization:');
disp(table(NAMES',mean(fracm)','VariableNames',{'Share' 'AverageUsage'}))
ribbon(fracm)
title('Share utilization')
set(gca,'XTick',[1:size(fracm,2)])
set(gca,'XTickLabel',NAMES)
set(gca,'YDir','reverse')
set(gca,'YTick',[1:9])
set(gca,'YTickLabel',[1:9]/10)
set(gca,'ZLim',[0,max(reshape(fracm,1,[]))]) Running the script will yield the following results and the graphic in Figure Share utilization.
Results
Estimated returns:
MaxRisk Return
_______ ______
0.1 0
0.2 11
0.3 13.3
0.4 15.6
0.5 17.8
0.6 19.9
0.7 21.1
0.8 22.3
0.9 23.5
Share utilization:
Share AverageUsage
_____________ ____________
'treasury' 0.16667
'hardware' 0.055556
'theater' 0.22222
'telecom' 0
'brewery' 0.033333
'highways' 0.2
'cars' 0
'bank' 0
'software' 0.2
'electronics' 0.011111 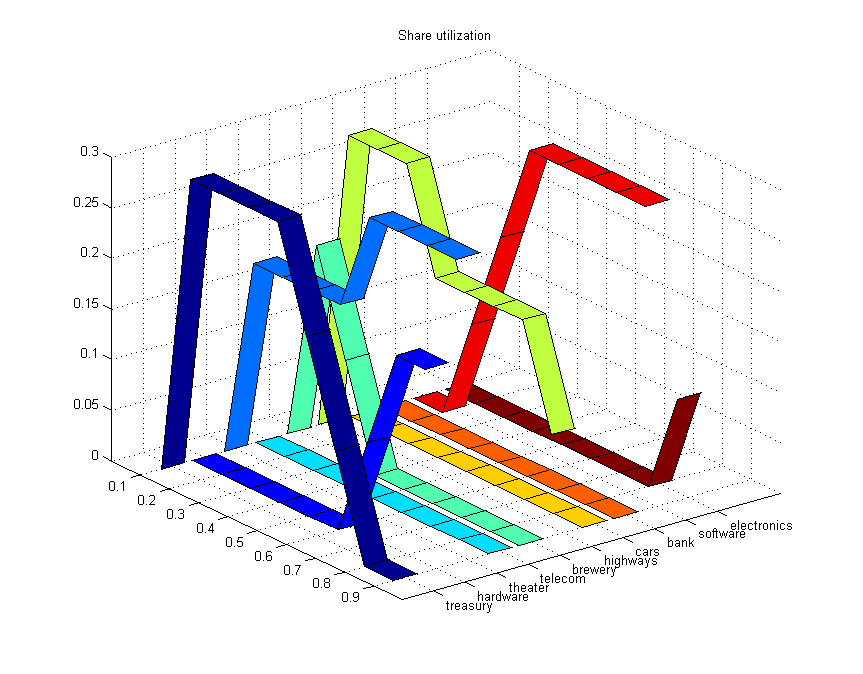
Figure 1.1: Share utilization

