Non-linear functions
Can model non-linear functions in the same way as incremental pricebreaks
- approximate the non-linear function with a piecewise linear function
- use an SOS2 to model the piecewise linear function
Non-linear function in a single variable
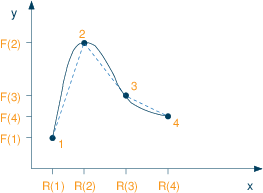
- x-coordinates of the points: R1, ..., R4
y-coordinates F1, ..., F4. So point 1 is (R1,F1) etc. - Let weights (decision variables) associated with point i be wi (i=1,...,4)
- Form convex combinations of the points using weights wi to get a combination point (x,y):
where the variables wi form an SOS2 set with ordering coefficients defined by values Ri.x = ∑i wi·Ri y = ∑i wi·Fi ∑i wi = 1 - Mosel implementation:
declarations I=1..4 x,y: mpvar w: array(I) of mpvar R,F: array(I) of real end-declarations ! ...assign values to arrays R and F... ! Define the SOS-2 with "reference row" coefficients from R Defx:= sum(i in I) R(i)*w(i) is_sos2 sum(i in I) w(i) = 1 ! The variable and the corresponding function value we want to approximate x = Defx y = sum(i in I) F(i)*w(i)
- BCL implementation:
XPRBprob prob("testsos"); XPRBvar x, y, w[I]; XPRBexpr Defx, le, ly; double R[I], F[I]; int i; // ...assign values to arrays R and F... // Create the decision variables x = prob.newVar("x"); y = prob.newVar("y"); for(i=0; i<I; i++) w[i] = prob.newVar("w"); // Define the SOS-2 with "reference row" coefficients from R for(i=0; i<I; i++) Defx += R[i]*w[i]; prob.newSos("Defx", XPRB_S2, Defx); for(i=0; i<I; i++) le += w[i]; prob.newCtr("One", le == 1); // The variable and the corresponding function value we want to approximate prob.newCtr("Eqx", x == Defx); for(i=0; i<I; i++) ly += F[i]*w[i]; prob.newCtr("Eqy", y == ly);
Non-linear function in two variables
Interpolation of a function f in two variables: approximate f at a point P by the corners C of the enclosing square of a rectangular grid (NB: the representation of P=(x,y) by the four points C obviously means a fair amount of degeneracy).
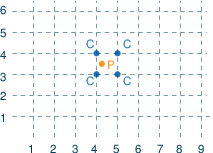
- x-coordinates of grid points: X1, ..., Xn
y-coordinates of grid points: Y1, ..., Ym. So grid points are (Xi,Yj). - Function evaluation at grid points: FXY11, ..., FXYnm
- Define weights (decision variables) associated with x and y coordinates, wxi respectively wyj, and for each grid point (X(i),Y(j)) define a variable wxyij
- Form convex combinations of the points using the weights to get a combination point (x,y) and the corresponding function approximation:
where the variables wxi form an SOS2 set with ordering coefficients defined by values Xi, and the variables wyj are a second SOS2 set with coordinate values Yj as ordering coefficients.x = ∑i wxi·Xi y = ∑j wyj·Yj f = ∑ij wxyij·FXYij ∀ i=1,...,n: ∑j wxyij = wxi ∀ j=1,...,m: ∑i wxyij = wyj ∑i wxi = 1 ∑j wyj = 1 - Mosel implementation:
declarations RX,RY:range X: array(RX) of real ! x coordinate values of grid points Y: array(RY) of real ! y coordinate values of grid points FXY: array(RX,RY) of real ! Function evaluation at grid points end-declarations ! ... initialize data declarations wx: array(RX) of mpvar ! Weight on x coordinate wy: array(RY) of mpvar ! Weight on y coordinate wxy: array(RX,RY) of mpvar ! Weight on (x,y) coordinates x,y,f: mpvar end-declarations ! Definition of SOS (assuming coordinate values <>0) sum(i in RX) X(i)*wx(i) is_sos2 sum(j in RY) Y(j)*wy(j) is_sos2 ! Constraints forall(i in RX) sum(j in RY) wxy(i,j) = wx(i) forall(j in RY) sum(i in RX) wxy(i,j) = wy(j) sum(i in RX) wx(i) = 1 sum(j in RY) wy(j) = 1 ! Then x, y and f can be calculated using x = sum(i in RX) X(i)*wx(i) y = sum(j in RY) Y(j)*wy(j) f = sum(i in RX,j in RY) FXY(i,j)*wxy(i,j) ! f can take negative or positive values (unbounded variable) f is_free
XPRBprob prob("testsos"); XPRBvar x, y, f; XPRBvar wx[NX], wy[NY], wxy[NX][NY]; // Weights on coordinates XPRBexpr Defx, Defy, le, lexy, lx, ly; double DX[NX], DY[NY]; double FXY[NX][NY]; int i,j; // ... initialize data arrays DX, DY, FXY // Create the decision variables x = prob.newVar("x"); y = prob.newVar("y"); f = prob.newVar("f", XPRB_PL, -XPRB_INFINITY, XPRB_INFINITY); // Unbounded variable for(i=0; i<NX; i++) wx[i] = prob.newVar("wx"); for(j=0; j<NY; j++) wy[j] = prob.newVar("wy"); for(i=0; i<NX; i++) for(j=0; j<NY; j++) wxy[i][j] = prob.newVar("wxy"); // Definition of SOS for(i=0; i<NX; i++) Defx += X[i]*wx[i]; prob.newSos("Defx", XPRB_S2, Defx); for(j=0; j<NY; j++) Defy += Y[j]*wy[j]; prob.newSos("Defy", XPRB_S2, Defy); // Constraints for(i=0; i<NX; i++) { le = 0; for(j=0; j<NY; j++) le += wxy[i][j]; prob.newCtr("Sumx", le == wx[i]); } for(j=0; j<NY; j++) { le = 0; for(i=0; i<NX; i++) le += wxy[i][j]; prob.newCtr("Sumy", le == wy[j]); } for(i=0; i<NX; i++) lx += wx[i]; prob.newCtr("Convx", lx == 1); for(j=0; j<NY; j++) ly += wy[j]; prob.newCtr("Convy", ly == 1); // Calculate x, y and the corresponding function value f we want to approximate prob.newCtr("Eqx", x == Defx); prob.newCtr("Eqy", y == Defy); for(i=0; i<NX; i++) for(j=0; j<NY; j++) lexy += FXY[i][j]*wxy[i][j]; prob.newCtr("Eqy", f == lexy);

