Problem description
The unit commitment problem consists in scheduling the power generation level of a set of generators to meet the power demand. In order for a power system to operate safely, the power generation must equal the demand at any time (the so-called power balance constraints) Failing to satisfy this requirement may result in serious issues, possibly causing a black out.
The power generation level of a power generating unit depends on its commitment. When the unit is switched off, no power is produced, only when it has been started the unit can generate electricity. Due to technical constraints, the power generation level must lie within a band describing safe operation. For the vast majority of unit types, the minimum power generation level is an important parameter when deciding whether to start a particular unit or not.
Another parameter that plays an important role in the decision whether to start a unit is its startup cost. Units with low startup cost could be started and shut down multiple times during a planning period, while units with high cost will preferrably be kept running once started.
For the sake of simplicity, other considerations like ramp rate constraints, shutdown costs or the various reserve types are omitted from the present model.
Example: We shall consider the case of day-head unit commitment scheduling. This operational planning task consists in determining on a day for the next, the startup and shutdown phases of the generating units in order to be able to safely satisfy the next day's power demand. However, the exact demand is not known for sure at the time of scheduling, and hence it is considered an uncertain parameter of the optimization problem. Common practice for dealing with this uncertainty is to commit a larger number of units than strictly required to be sure to have sufficient upward and downward power generation reserve. In the following we will show how to apply robust optimization techniques to take into account this uncertainty more efficiently.
We are going to present two robust implementations of the unit commitment problem resulting in plans for which the unit commitment decisions do not have to be changed in real time. More precisely, the suggested unit commitment schedules make sure that enough power generation capacity is available to supply the actual demand without requiring any last minute unit startups or shutdowns. The first model is based on a scenario uncertainty set, it ensures that the unit commitment status will not require any modification even if the real power demand is different from the forecast. In this problem it is assumed that the power demand realization will be similar to either the forecast or some historical power demand curve. The second model, based on a cardinality uncertainty set, guarantees that the unit commitment status will not require any modification even if up to 'k' generating units are simultaneously forced in outage.
Robust against power demand variation
Typical unit commitment robustness against power demand variation is achieved by adding constraints to bound the difference between the total power generation and the total available power generation capacity of running units. This value is known as the upward power generation level and defines the maximum power demand increase that can be safely supplied without requiring new unit startup. This empirical value is arbitrarly determined from historical power demand.
We will see how the robust optimization framework can be used to seamlessly implement similar constraints by replacing the reserve requirement by a set of robust constraints formed from historical power demand. These historical data and the power demand forecast are used to determine the real power demand. This real power demand is modeled with the scenario uncertainty sets. The figure Historical power demand and forecast presents the next day's historical power demand of the last 6 years alongside with the forecasted power demand.
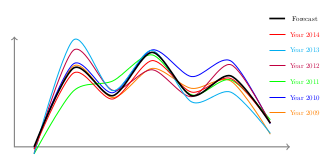
Figure 6: Historical power demand and forecast
Robust against the N-k contingency
Typical unit commitment robustness against unit forced outage is achieved by analysing the impact of a contingency resulting in loss of k generating units. If the total lost generation is greater than the upward reserve from the remaining generating units, then the system is at risk and demand cannot be fully sustained. Running such a simulation is an important task and provides insights about the security of the power system. Unfortunately, if it can prove the inability of the schedule to survive k, the model will fail to suggest how to improve the schedule to satisfy the safety constraint.
A robust optimization formulation can be used to simulate the loss of k running units and to suggest the startup and shutdown of new units to safely supply the power demand. The cardinality uncertainty sets will be used to model the outage state of a unit.

