abs and distance: Frequency assignment
The area of telecommunications, and in particular mobile telecommunications, gives rise to many different variants of frequency assignment problems.
We are given a network of cells (nodes) with requirements of discrete frequency bands. Each cell has a given demand for a number of frequencies (bands). Figure Telecommunications network shows the structure of the network. Nodes linked by an edge are considered as neighbors. They must not be assigned the same frequencies to avoid interference. Furthermore, if a cell uses several frequencies they must all be different by at least 2. The objective is to minimize the total number of frequencies used in the network.
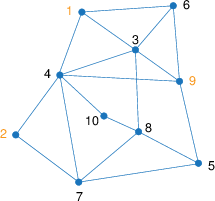
Figure 3.1: Telecommunications network
Table Frequency demands at nodes lists the number of frequency demands for every cell.
| Cell | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Demand | 4 | 5 | 2 | 3 | 2 | 4 | 3 | 4 | 3 | 2 |
Model formulation
Let NODES be the set of all nodes in the network and DEMn the demand of frequencies at node n ∈ NODES. The network is given as a set of edges LINKS. Furthermore, let DEMANDS = {1,2,...,NUMDEM} be the set of frequencies, numbered consecutively across all nodes where the upper bound NUMDEM is given by the total number of demands. The auxiliary array INDEXn indicates the starting index in DEMANDS for node n.
For representing the frequency assigned to every demand d ∈ DEMANDS we introduce the variables used that take their values from the set {1,2,...,NUMDEM}.
The two sets of constraints (different frequencies assigned to neighboring nodes and minimum distance between frequencies within a node) can then be modeled as follows.
| INDEXn+DEMn-1 |
| ⋃ |
| d=INDEXn |
| INDEXm+DEMm-1 |
| ⋃ |
| d=INDEXm |
∀ n ∈ NODES, ∀ c<d ∈ INDEXn,...,INDEXn+DEMn-1: |usec - used| ≥ 2
The objective function is to minimize to the number of frequencies used. We formulate this by minimizing the largest frequency number that occurs for the used variables:
Implementation
The edges forming the telecommunications network are modeled as a list LINK, where edge l is given as (LINK(l,1),LINK(l,2)).
For the implementation of the constraints on the values of frequencies assigned to the same node we have two equivalent choices with Kalis, namely using abs or distance constraints.
model "Frequency assignment"
uses "kalis"
forward procedure print_solution
declarations
NODES = 1..10 ! Range of nodes
LINKS = 1..18 ! Range of links between nodes
DEM: array(NODES) of integer ! Demand of nodes
LINK: array(LINKS,1..2) of integer ! Neighboring nodes
INDEX: array(NODES) of integer ! Start index in 'use'
NUMDEM: integer ! Upper bound on no. of freq.
end-declarations
DEM :: (1..10)[4, 5, 2, 3, 2, 4, 3, 4, 3, 2]
LINK:: (1..18,1..2)[1, 3, 1, 4, 1, 6,
2, 4, 2, 7,
3, 4, 3, 6, 3, 8, 3, 9,
4, 7, 4, 9, 4,10,
5, 7, 5, 8, 5, 9,
6, 9, 7, 8, 8,10]
NUMDEM:= sum(n in NODES) DEM(n)
! Correspondence of nodes and demand indices:
! use(d) d = 1, ..., DEM(1) correspond to the demands of node 1
! d = DEM(1)+1, ..., DEM(1)+DEM(2)) - " - node 2 etc.
INDEX(1):= 1
forall(n in NODES | n > 1) INDEX(n) := INDEX(n-1) + DEM(n-1)
declarations
DEMANDS = 1..NUMDEM ! Range of frequency demands
use: array(DEMANDS) of cpvar ! Frequency used for a demand
numfreq: cpvar ! Number of frequencies used
Strategy: array(range) of cpbranching
end-declarations
! Setting the domain of the decision variables
forall(d in DEMANDS) setdomain(use(d), 1, NUMDEM)
! All frequencies attached to a node must be different by at least 2
forall(n in NODES, c,d in INDEX(n)..INDEX(n)+DEM(n)-1 | c<d)
distance(use(c), use(d)) >= 2
! abs(use(c) - use(d)) >= 2
! Neighboring nodes take all-different frequencies
forall(l in LINKS)
all_different(
union(d in INDEX(LINK(l,1))..INDEX(LINK(l,1))+DEM(LINK(l,1))-1) {use(d)} +
union(d in INDEX(LINK(l,2))..INDEX(LINK(l,2))+DEM(LINK(l,2))-1) {use(d)},
KALIS_GEN_ARC_CONSISTENCY)
! Objective function: minimize the number of frequencies used, that is,
! minimize the largest value assigned to 'use'
setname(numfreq, "NumFreq")
numfreq = maximum(use)
! Search strategy
Strategy(1):=assign_var(KALIS_SMALLEST_DOMAIN, KALIS_MIN_TO_MAX, use)
Strategy(2):=assign_var(KALIS_MAX_DEGREE, KALIS_MIN_TO_MAX, use)
cp_set_branching(Strategy(1))
setparam("KALIS_MAX_COMPUTATION_TIME", 1)
cp_set_solution_callback("print_solution")
! Try to find solution(s) with strategy 1
if (cp_minimize(numfreq)) then
cp_show_stats
sol:=getsol(numfreq)
end-if
! Restart search with strategy 2
cp_reset_search
if sol>0 then ! If a solution was found:
numfreq <= sol-1 ! Add upper bound on objective
end-if
cp_set_branching(Strategy(2))
setparam("KALIS_MAX_COMPUTATION_TIME", 1000)
if (cp_minimize(numfreq)) then
cp_show_stats
elif sol>0 then
writeln("Optimality proven")
else
writeln("Problem has no solution")
end-if
!********************************************************************
! **** Solution printout ****
procedure print_solution
writeln("Number of frequencies: ", getsol(numfreq))
writeln("Frequency assignment: ")
forall(n in NODES) do
write("Node ", n, ": ")
forall(d in INDEX(n)..INDEX(n)+DEM(n)-1) write(getsol(use(d)), " ")
writeln
end-do
end-procedure
end-model
With just the default search strategy this model finds a solution of value 11 but it runs for a long time without being able to prove optimality. When experimenting with different search strategies we have found that the strategy obtained by changing the variable selection criterion to KALIS_MAX_DEGREE is able to prove optimality easily once a good solution is known. This problem is therefore solved in two steps: First, we use the default strategy for finding a good solution. This search is stopped after one second by setting a time limit. The search is then restarted (previously, we needed to reset the search tree in the solver with cp_reset_search) with a second strategy and the bound on the objective value from the previous run.
To ease the experiments with different search strategies we have defined an array Strategy of type cpbranching that stores the different search strategy definitions.
Another new feature demonstrated by this implementation is the use of a callback, more precisely the solution callback of Xpress Kalis. The solution callback is defined with a user subroutine that will be called by the solver whenever the search has found a solution. Its typical uses are logging or storing of intermediate solutions or performing some statistics. Our procedure print_solution simply prints out the solution that has been found.
Improving the problem formulation: we may observe that in our problem formulation all demand variables within a node and the constraints on these variables are entirely symmetric. In the absence of other constraints, we may reduce these symmetries by imposing an order on the use variables,
for demands d and d+1 belonging to the same cell. Doing so, the problem is solved to optimality within less than 40 nodes using just the default strategy. We may take this a step further by writing
The addition of these constraints shortens the search by yet a few more nodes. They can even be used simply in replacement of the abs or distance constraints.
Results
An optimal solution to this problem uses 11 different frequencies. The model shown in the program listing prints out the following assignment of frequencies to nodes:
Node 1: 1 3 5 7 Node 2: 1 3 5 7 10 Node 3: 2 8 Node 4: 4 6 9 Node 5: 4 6 Node 6: 4 6 9 11 Node 7: 2 8 11 Node 8: 1 3 5 7 Node 9: 1 3 5 Node 10: 2 8

