distribute: Personnel planning

The director of a movie theater wishes to establish a plan with the working locations for his personnel. The theater has eight employees: David, Andrew, Leslie, Jason, Oliver, Michael, Jane, and Marilyn. The ticket office needs to be staffed with three persons, theater entrances one and two require two persons each, and one person needs to be put in charge of the cloakroom. Due to different qualifications and respecting individual likes and dislikes, the following constraints need to be taken into account:

1. Leslie must be at the second entrance of the theater.
2. Michael must be at the first entrance of the theater.
3. David, Michael and Jason cannot work with each other.
4. If Oliver is selling tickets, Marylin must be with him.

Model formulation

Let PERS be the set of personnel and LOC = {1,...,4} the set of working locations where 1 stands for the ticket office, 2 and 3 for entrances 1 and 2 respectively, and 4 for the cloakroom.

We introduce decision variables place_p for the working location assigned to person p. The four individual constraints on working locations can then be stated as follows:

We also have to meet the staffing requirement of every working location:

Implementation

For the implementation of the staffing requirements we may choose among two different constraints of Xpress Kalis, namely occurrence constraints (one per working location) or a distribute constraint (also known as global cardinality constraint) over all working locations. The following model shows both options. As opposed to the previous example (Section Implementation we now have equality constraints. We therefore use the three-argument version of distribute (instead of the version with four arguments where the last two are the lower and upper bounds respectively).

For an attractive display, the model also introduces a few auxiliary data structures with the names of the working locations and the corresponding index values in the set LOC.

model "Personnel Planning (CP)"
 uses "kalis"

 forward procedure print_solution

 declarations
  PERS = {"David","Andrew","Leslie","Jason","Oliver","Michael",
          "Jane","Marilyn"}                ! Set of personnel
  LOC = 1..4                               ! Set of locations
  LOCNAMES = {"Ticketoffice", "Theater1", "Theater2",
              "Cloakroom"}                 ! Names of locations
  LOCNUM: array(LOCNAMES) of integer       ! Numbers assoc. with loc.s
  REQ: array(LOC) of integer               ! No. of pers. req. per loc.

  place: array(PERS) of cpvar              ! Workplace assigned to each peson
 end-declarations

! Initialize data
 LOCNUM("Ticketoffice"):= 1; LOCNUM("Theater1"):= 2
 LOCNUM("Theater2"):= 3; LOCNUM("Cloakroom"):= 4
 REQ:: (1..4)[3, 2, 2, 1]

! Each variable has a lower bound of 1 (Ticketoffice) and an upper bound
! of 4 (Cloakroom)
 forall(p in PERS) do
  setname(place(p),"workplace["+p+"]")
  setdomain(place(p), LOC)
 end-do

! "Leslie must be at the second entrance of the theater"
 place("Leslie") = LOCNUM("Theater2")

! "Michael must be at the first entrance of the theater"
 place("Michael") = LOCNUM("Theater1")

! "David, Michael and Jason cannot work with each other"
 all_different({place("David"), place("Michael"), place("Jason")})

! "If Oliver is selling tickets, Marylin must be with him"
 implies(place("Oliver")=LOCNUM("Ticketoffice"),
         place("Marilyn")=LOCNUM("Ticketoffice"))
	
! Creation of a resource constraint of for every location
! forall(d in LOC) occurrence(LOCNUM(d), place) = REQ(d)

! Formulation of resource constraints using global cardinality constraint
 distribute(place, LOC, REQ)

! Setting parameters of the enumeration
 cp_set_branching(assign_var(KALIS_SMALLEST_MIN, KALIS_MAX_TO_MIN, place))

! Solve the problem
 if not(cp_find_next_sol) then
  writeln("Problem is infeasible")
  exit(1)
 end-if

! Solution output
 nbSolutions:= 1
 print_solution

! Search for other solutions
 while (cp_find_next_sol) do
  nbSolutions += 1
  print_solution
 end-do

! **** Solution printout ****
 procedure print_solution
  declarations
   LOCIDX: array(LOC) of string
  end-declarations
  forall(l in LOCNAMES) LOCIDX(LOCNUM(l)):=l

  writeln("\nSolution number ", nbSolutions)
  forall(p in PERS)
   writeln(" Working place of ", p, ": ", LOCIDX(getsol(place(p))))
 end-procedure

end-model

Since we merely wish to find a feasible assignment of working locations, this model first tests whether a feasible solution exists. If this is the case, it also enumerates all other feasible solutions. Each time a solution is found it is printed out by call to the procedure print_solution.

Results

This problem has 38 feasible solutions. A graphical representation of a feasible assignment is shown in Figure Personnel schedule representation.

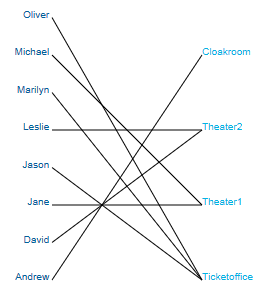
Figure 3.2: Personnel schedule representation

The following Mosel code was used for generating the graphic (see the documentation of module mmsvg in the Mosel language reference manual for further explanation).

! **** Solution printout and graphical display ****
 procedure draw_solution
  svgerase
  svgaddgroup("PersGraph", "Personnel")
  svgsetstyle(SVG_TEXTANCHOR, "end")
  svgaddgroup("LocGraph", "Locations")
  svgaddgroup("AsgnGraph", "Assignments", SVG_BLACK)

  forall(d in LOCNAMES)
   svgaddtext("LocGraph", 4, LOCNUM(d), d)

  FACT:=LOCNAMES.size/PERS.size
  idx:= 1
  forall(p in PERS, idx as counter) do
   svgaddline("AsgnGraph", 2, idx*FACT, 4, getsol(place(p)))
   svgaddtext("PersGraph", 2, idx*FACT, p)
  end-do

  svgsetgraphscale(75)
  svgsetgraphviewbox(0,0,5,LOCNAMES.size+1)
  svgrefresh

  ! Uncomment to pause at every iteration:
  if nbSolutions<MAXSOL then svgpause; end-if
 end-procedure