Convexity
Convex problems have many desirable characteristics from the perspective of mathematical optimization. Perhaps the most significant of these is that should both the objective and the feasible region be convex, any local optimally solutions found are also known immediately to be globally optimal.
A constraint f(x)≤0 is convex if the matrix of second derivatives of f, that is to say its Hessian, is positive semi-definite at every point at which it exists. This requirement can be understood geometrically as requiring every point on every line segment which connects two points satisfying the constraint to also satisfy the constraint. It follows trivially that linear functions always lead to convex constraints, and that a nonlinear equality constraint is never convex.
Figure 7.1: Two convex functions on the left, and two non-convex functions on the right.
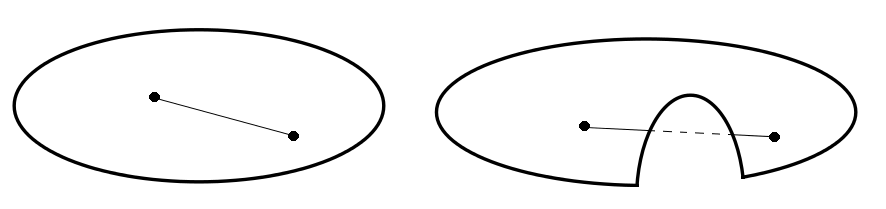
For regions, a similar property must hold. If any two points of the region can be connected by a line segment which lies fully in the region itself, the region is convex. This extension is straightforward when the the properties of convex functions are considered.
Figure 7.2: A convex region on the left and a non-convex region on the right.
It is important to note that convexity is necessary for some solution techniques and not for others. In particular, some solvers require convexity of the constraints and objective function to hold only in the feasible region, whilst others may require convexity to hold across the entire space, including infeasible points. In the special case of quadratic and quadratically constrained programs, Xpress NonLinear seamlessly migrates problems to solvers whose convexity requirements match the convexity of the problem.