Problem Formulation
This formulation is one of two described by Prieto [1]. It is easy to visualize, and has advantages in later examples. The pentagon is about the smallest model which can reasonably be used – it is non-trivial but is still just about small enough to be written out in full.
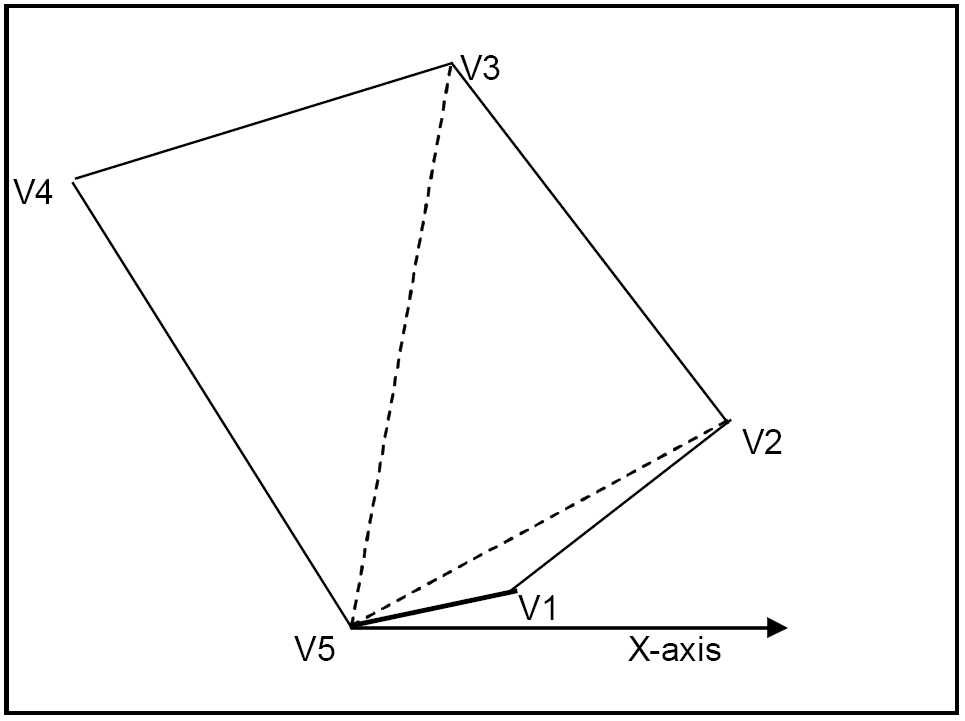
Figure 2.1: Polygon Example
One vertex (the highest-numbered, VN) is chosen as the "base" point, and all the other vertices are measured from it, using (r,θ) coordinates – that is, the distance ("r") is measured from the vertex, and the angle or bearing of the vertex ("θ") is measured from the X-axis.
We shall use ri and θi as the coordinates of vertex Vi. Then simple geometry and trigonometry gives:
- The area of the triangle VNViVj: area(VNViVj) =
· ri · rj · sin(θj-θi)1 2 - The side ViVj is given by: (ViVj)2 = ri2 + rj2 - 2·ri·rj·cos(θj-θi)
- The total area of the polygon is: ∑i=2N-1 area(VNViVi-1)
- The maximum diameter of 1 requires that all the sides of all the triangles are ≤ 1 – that is:
ri ≤ 1 for i=1,...,N-1
and
ViVj ≤ 1 for i=1,...,N-2, j=i+1,...,N-1
We have assumed in the diagram Polygon Example and in the formulation that θi≤θi+1 – in other words, the vertices are in order anti-clockwise. In fact, this is not just an assumption, and we need to include these constraints as well.
In the diagram, we have assumed that the first angle θ1 is ≥ 0. This is not an additional restriction if we use the normal modeling convention that all variables are non-negative. We also assumed that the last vertex is still "above" the X-axis – that is, θN-1 is ≤ 180° (or π radians).
The requirement is therefore:
| maximize | ∑i=2N-1(ri · ri-1 · sin(θi-θi-1))*0.5 | (area of the polygon) |
| subject to: | ri ≤ 1 for i=1,...,N-1 | (distances betweem VN and other vertices) |
| ri2 + rj2 - 2·ri·rj·cos(θj-θi ≤ 1 for i=1,...,N-2, j=i+1,...,N-1 | ||
| (distances between other pairs of vertices) | ||
| θ1 ≥ 0 | (first bearing is non-negative) | |
| θi+1 - θi ≥ 0 for i=1,...,N-2 | (bearings are in order) | |
| θN-1 ≤ π | (last vertex is above X-axis) | |
Reference:
(1) F.J. Prieto. Maximum area for unit-diameter polygon of N sides, first model and second model (Netlib AMPL programs in ftp://netlib.bell-labs.com/netlib/ampl/models).

