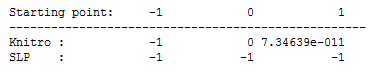Points of inflection
A point of inflection in a given variable occurs when the first and second order partial derivatives with respect to that variable become zero, but there exist nonzero derivatives of higher order. At such points, the approximations the iterative nonlinear methods create do not encapsulate enough information about the behavior of the function, and both first and second order methods may experience difficulties. For example, consider the following problem
| minimize | x3 |
| subject to | -1≤x≤1 |
When the initial value of x is varied, XSLP and Knitro produce the solutions presented in Table Effect of an inflection point on solution values. for this problem:
Figure 9.1: Effect of an inflection point on solution values.
As a second order method, Knitro examines a local quadratic approximation to the function. Starting at both 0 and 1, this approximation will closely resemble the x^2 function, and so the solution will be attracted to zero. For XSLP, which is a first order method, the approximation at 0 will have a zero gradient. However, XSLP can detect this situation and will perform the analysis required to substitute an appropriate small nonzero (placeholder) value for the derivative during the first iterations. As can be seen, this allows XSLP find an optimal solution in all three cases.
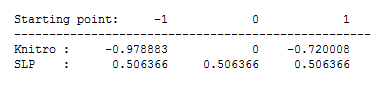
This is only one example of the behaviour of these solvers without further tuning. The long steps which XSLP often takes can be both beneficial and harmful in different contexts. For example, if the function to be optimized includes many local minima, it is possible to see the opposite pattern for XSLP and Knitro. Consider
| minimize | x |
| subject to | -1≤x≤1 |
Figure 9.2: Local solutions for a function with several local optima
In this case the same long steps made by XSLP lead to it finding the an identical, but unfortunate, local optimum no matter which initial point it begins from.