Problem Formulation
This formulation is one of two described by Prieto [1]. It is easy to visualize, and has advantages in later examples. The pentagon is about the smallest model which can reasonably be used – it is non-trivial but is still just about small enough to be written out in full.
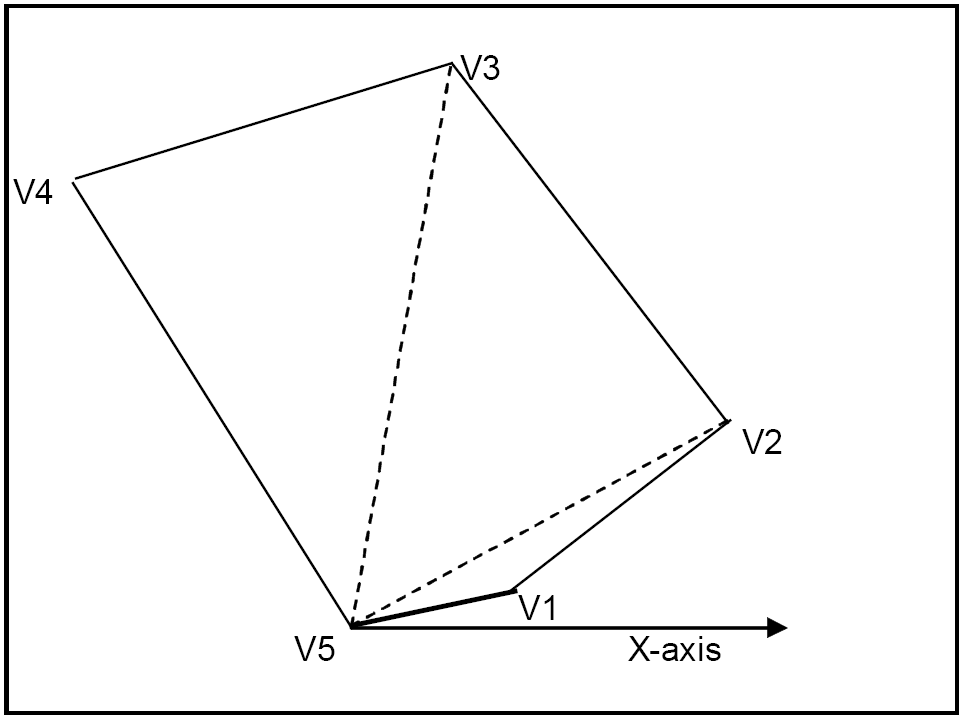
Figure 2.1: Polygon Example
One vertex (the highest-numbered, VN) is chosen as the "base" point, and all the other vertices are measured from it, using (r,θ) coordinates – that is, the distance ("r") is measured from the vertex, and the angle or bearing of the vertex ("θ") is measured from the X-axis.
We shall use ri and θi as the coordinates of vertex Vi. Then simple geometry and trigonometry gives:
- The area of the triangle VNViVj: area(VNViVj) =
· ri · rj · sin(θj-θi)1 2 - The side ViVj is given by: (ViVj)2 = ri2 + rj2 - 2·ri·rj·cos(θj-θi)
- The total area of the polygon is: ∑i=2N-1 area(VNViVi-1)
- The maximum diameter of 1 requires that all the sides of all the triangles are ≤ 1 – that is:
ri ≤ 1 for i=1,...,N-1
and
ViVj ≤ 1 for i=1,...,N-2, j=i+1,...,N-1
We have assumed in the diagram Polygon Example and in the formulation that θi≤θi+1 – in other words, the vertices are in order anti-clockwise. In fact, this is not just an assumption, and we need to include these constraints as well.
In the diagram, we have assumed that the first angle θ1 is ≥ 0. This is not an additional restriction if we use the normal modeling convention that all variables are non-negative. We also assumed that the last vertex is still "above" the X-axis – that is, θN-1 is ≤ 180° (or π radians).
The requirement is therefore:
| maximize | ∑i=2N-1(ri · ri-1 · sin(θi-θi-1))*0.5 | (area of the polygon) |
| subject to: | ri ≤ 1 for i=1,...,N-1 | (distances betweem VN and other vertices) |
| ri2 + rj2 - 2·ri·rj·cos(θj-θi ≤ 1 for i=1,...,N-2, j=i+1,...,N-1 | ||
| (distances between other pairs of vertices) | ||
| θ1 ≥ 0 | (first bearing is non-negative) | |
| θi+1 - θi ≥ 0 for i=1,...,N-2 | (bearings are in order) | |
| θN-1 ≤ π | (last vertex is above X-axis) | |
Reference:
(1) F.J. Prieto. Maximum area for unit-diameter polygon of N sides, first model and second model (Netlib AMPL programs in ftp://netlib.bell-labs.com/netlib/ampl/models).
© 2001-2019 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

