Basic concepts of Constraint Programming

A Constraint Programming (CP) problem is defined by its decision variables with their domains and constraints over these variables. The problem definition is usually completed by a branching strategy (also referred to as enumeration or search strategy).

CP makes active use of the concept of variable domains, that is, the set out of which a decision variable takes its values. In finite domain Constraint Programming these are sets or intervals of integer numbers.

Each constraint in CP comes with its own (set of) solution algorithm(s), typically based on results from other areas, such as graph theory. Once a constraint has been established it maintains its set of variables in a solved state, i.e., its solution algorithm removes any values that it finds infeasible from the domains of the variables.

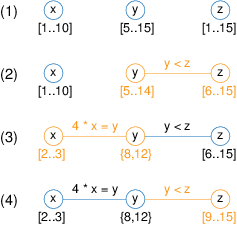
The constraints in a CP problem are linked by a mechanism called constraint propagation: whenever the domain of a variable is modified this triggers a re-evaluation of all constraints on this variable which in turn may cause modifications to other variables or further reduction of the domain of the first variable as shown in the example in Figure Example of constraint propagation, (a) finite domain (discrete) variables, (b) continuous variables. (the original domains of the variables are reduced by the addition of two constraints; in the last step the effect of the second constraint is propagated to the first constraint, triggering its re-evaluation).

(a)			(b)

Figure 1.1: Example of constraint propagation, (a) finite domain (discrete) variables, (b) continuous variables.

A CP problem is built up incrementally by adding constraints and bounds on its variables. The solving of a CP problem starts with the statement of the first constraint—values that violate the constraint relation are removed from the domains of the involved variables. Since the effect of a newly added constraint is propagated immediately to the entire CP problem it is generally not possible to modify or delete this constraint from the problem later on.

In some cases the combination of constraint solving and the propagation mechanism may be sufficient to prove that a problem instance is infeasible, but most of the time it will be necessary to add an enumeration for reducing all variable domains to a single value (consistent instantiation or feasible solution) or proving that no such solution exists. In addition it is possible to define an objective function (or cost function) and search for a feasible solution with the best objective function value (optimal solution).