Working with lists

Enumeration

Similarly to the way we have used sets so far, lists may be used as loop indices for enumeration. The following enumerates a given list L from beginning to end:

 declarations
  L: list of integer
 end-declarations

 L:= [1,2,3,4,5]

 forall(i in L) writeln(i) 

Since lists have an ordering we may choose, for instance, to reverse the order of list elements for the enumeration. The model listenum.mos below shows several possibilities for enumerating lists in inverse order: (1) reversing a copy of the list to enumerate, (2) reversing the list to enumerate. In the first case we obtain the reversed copy of the list with function getreverse, in the second case we modify the original list by applying to it the procedure reverse.

model "Reversing lists"

 declarations
  K,L: list of integer
 end-declarations

 L:= [1,2,3,4,5]

! Enumeration in inverse order:
 ! 1. Reversed copy of the list (i.e., no change to 'L')
 K:=getreverse(L)
 forall(i in K) writeln(i)

 ! 2. Reversing the list itself
 reverse(L)
 forall(i in L) writeln(i)

end-model 

List operators

Lists are composed by concatenating several lists or by truncating their extremities (refered to as head and tail). The operators += and + serve for concatenating lists. Their inverses (-= and -) may be used to remove the tail of a list—they will not remove the given sublist if it is not positioned at the end.

The following model listops.mos shows some examples of the use of list operators. Besides the concatenation operators + and += we also use the aggregate form sum. Another list operator used in this example is the comparison operator <> (the comparison operator = may also be used with lists).

model "List operators"

 declarations
  L,M: list of integer
 end-declarations

 L:= [1,2,3] + [4,5]; writeln("L (1): ", L)
 L+= [6,7,8]; writeln("L (2): ", L)
 L-= [1,2,3]; writeln("L (3): ", L)

 M:= sum(l in L) [l*2]; writeln("M: ", M)

 writeln("L and M are different: ", L<>M)

end-model 

As can be seen in the output, the list [1,2,3] is not removed from L since it is not located at its tail:

L (1): [1,2,3,4,5]
L (2): [1,2,3,4,5,6,7,8]
L (3): [1,2,3,4,5,6,7,8]
M: [2,4,6,8,10,12,14,16]
L and M are different: true 

List handling functions

The Mosel subroutines for list handling form two groups, namely

• Operations preserving the list they are applied to: retrieving a list element (getelt, getfirst, getlast), occurrence of an element (findfirst, findlast), retrieving a copy of the head or tail (gethead, gettail), reversed copy of a list (getreverse)
• Operations modifying the list they are applied to: cutting off (=discard) individual elements or the head or tail (cutelt, cutfirst, cutlast, cuthead, cuttail), splitting off (=retrieve) the head or tail (splithead, splittail), reverse the list (reverse)

The following example listmerge.mos merges two lists of integers K and L, the elements of which are ordered in increasing order of their values into a new list M that is ordered in the same way. The elements of the two original lists are added one-by-one to the new list using the concatenation operator +=. Whilst the elements of the list K are simply enumerated, we iteratively split off the first element from list L (using splithead with second argument 1 to take away just the first list element) so that this list will be empty at the end of the forall loop. If this is not desired, we need to work with a copy of this list.

model "Merging lists"

 declarations
  K,L,M: list of integer
 end-declarations

 K:= [1,4,5,8,9,10,13]
 L:= [-1,0,4,6,7,8,9,9,11,11]

 forall(k in K) do
  while (L<>[] and k >= getfirst(L))  M += splithead(L,1)
  M+= [k]
 end-do

 writeln(M)

end-model 

The resulting list M is:

[-1,0,1,4,4,5,6,7,8,8,9,9,9,10,11,11,13] 

List handling routines provide a powerful means of programming, illustrated by the following example euler.mos that constructs a Eulerian circuit for the network shown in Figure Network forming a Eulerian circuit (thick arrows indicate that the corresponding arc is to be used twice). This example is an alternative implementation of the Eulerian circuit algorithm described in Section 15.4 `Gritting roads' (problem j4grit) of the book 'Applications of optimization with Xpress-MP'.

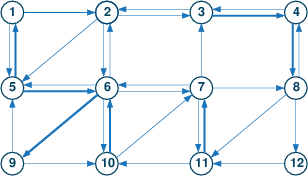
Figure 10.1: Network forming a Eulerian circuit

A Eulerian circuit is a tour through a network that uses every given arc exactly once. To construct such a circuit for a given set of arcs we may employ the following algorithm

• Choose a start node and add it to the tour.
• while there are unused arcs:
  – Find the first node in the tour with unused outgoing arcs.
  – Construct a closed subtour starting from this node.
  – Insert the new subtour into the main tour.

model "Eulerian circuit"

 declarations
  NODES = 1..12                        ! Set of nodes
  UNUSED: array(NODES) of list of integer
  TOUR: list of integer
  NEWT, TAIL: list of integer
 end-declarations

 initializations from 'euler.dat'
  UNUSED
 end-initializations

 ct:=sum(i in NODES) getsize(UNUSED(i))

 TOUR:=[1]                            ! Choose node 1 as start point

 while(ct>0) do                       ! While there are unused arcs:
     ! Find first node in TOUR with unused outgoing arc(s)
  node:=0
  forall(i in TOUR)
   if UNUSED(i) <> [] then
    node:=i
    break
   end-if

     ! Insertion position (first occurrence of 'node' in TOUR)
  pos:= findfirst(TOUR, node)

     ! Construct a new subtour starting from 'node'
  cur:=node                           ! Start with current node
  NEWT:=[]
  while(UNUSED(cur) <> []) do
   NEWT+=splithead(UNUSED(cur),1)     ! Take first unused arc
   cur:=getlast(NEWT)                 ! End point of arc is new current node
  end-do

     ! Stop if the subtour is not a closed loop (=> no Eulerian circuit)
  if cur<>node then                   ! Compare start and end of subtour
   writeln("Tour cannot be closed")
   exit(1)
  end-if

     ! Add the new subtour to the main journey
  TAIL:=splittail(TOUR, -pos)         ! Split off the tail from main tour
  TOUR += NEWT + TAIL                 ! Attach subtour and tail to main tour
  ct -= getsize(NEWT)
 end-do

 writeln("Tour: ", TOUR)              ! Print the result

end-model 

The data file euler.dat corresponding to the graph in Figure Network forming a Eulerian circuit has the following contents:

UNUSED: [(1) [2 5] (2) [3 5 6] (3) [2 4 4] (4) [3 8 8]
         (5) [1 1 6 6] (6) [2 5 7 9 9 10] (7) [3 6 8 11]
         (8) [4 11 12] (9) [5 10] (10) [6 6 7]
         (11) [7 7 10] (12) [11] ] 

A Eulerian circuit for this data set is the tour

1 → 2 → 6 → 5 → 6 → 7 → 8 → 12 → 11 → 7 → 11 → 10 → 7 → 3 → 4 → 3 → 4 → 8 → 4 → 8 → 11 → 7 → 6 → 9 → 5 → 6 → 9 → 10 → 6 → 10 → 6 → 2 → 3 → 2 → 5 → 1 → 5 → 1