Price breaks

All items discount: when buying a certain number of items we get discounts on all items that we buy if the quantity we buy lies in certain price bands.


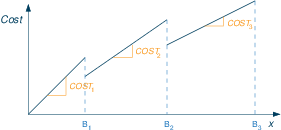
less than B₁	COST₁ each
≥ B₁ and < B₂	COST₂ each
≥ B₂ and < B₃	COST₃ each

Define binary variables b_i (i=1,2,3), where b_i is 1 if we pay a unit cost of COST_i.
Real decision variables x_i represent the number of items bought at price COST_i.
The quantity bought is given by x= ∑_ixp_i , with a total price of ∑_iCOST_i·xp_i
MIP formulation :

∑_i b_i = 1

xp₁ ≤ B₁· b₁

B_i-1· b_i ≤ xp_i ≤ B_i· b_i for i=2,3

where the variables b_i are either defined as binaries, or they form a Special Ordered Set of type 1 (SOS1), where the order is given by the values of the breakpoints B_i.

∑_i b_i = 1
xp₁ ≤ B₁· b₁
B_i-1· b_i ≤ xp_i ≤ B_i· b_i for i=2,3

Incremental pricebreaks: when buying a certain number of items we get discounts incrementally. The unit cost for items between 0 and B₁ is C₁, items between B₁ and B₂ cost C₂ each, etc.

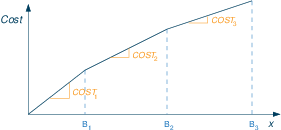
Formulation with Special Ordered Sets of type 2 (SOS2):

Associate real valued decision variables w_i (i=0,1,2,3) with the quantity break points B₀ = 0, B₁, B₂ and B₃.
Cost break points CBP_i (=total cost of buying quantity B_i):

CBP₀=0

CBP_i = CBP_i-1+C_i· (B_i-B_i-1) for i=1,2,3
Constraint formulation:

∑_iw_i=1

TotalCost = ∑_i CBP_i· w_i

x = ∑_i B_i· w_i

where the w_i form a SOS2 with reference row coefficients given by the coefficients in the definition of the total amount x.
For a solution to be valid, at most two of the w_i can be non-zero, and if there are two non-zero they must be contiguous, thus defining one of the line segments.
Implementation with Mosel (is_sos2 cannot be used here due to the 0-valued coefficient of w₀):
```
Defx := x = sum(i in 1..3) B(i)*w(i)
makesos2(My_Set, union(i in 0..3) {w(i)}, Defx)
```

CBP₀=0
CBP_i = CBP_i-1+C_i· (B_i-B_i-1) for i=1,2,3

∑_iw_i=1
TotalCost = ∑_i CBP_i· w_i
x = ∑_i B_i· w_i

Formulation using binaries:

Define binary variables b_i (i=1,2,3), where b_i is 1 if we have bought any items at a unit cost of COST_i.
Real decision variables x_i (i=1,..3) for the number of items bought at price COST_i.
Total amount bought: x = ∑_i x_i
Constraint formulation:

(B_i-B_i-1)\cdot b_i+1 ≤ x_i ≤ (B_i-B_i-1)\cdot b_i for i=1,2

x₃ ≤ (B₃-B₂)\cdot b₃

b₁ ≥ b₂ ≥ b₃

(B_i-B_i-1)\cdot b_i+1 ≤ x_i ≤ (B_i-B_i-1)\cdot b_i for i=1,2
x₃ ≤ (B₃-B₂)\cdot b₃
b₁ ≥ b₂ ≥ b₃

© 2001-2020 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

Contents

Index

Glossary

Search Results

Price breaks