Enumeration and search strategy
Since the combination of constraint solving and propagation mechanism is usually not sufficient to reduce all variable domains to a single value, an enumeration needs to be added to the problem definition to find feasible solutions or to prove that no such solution exists.
The search process is made by a branch and bound algorithm with depth-first exploration of the search tree. At each node, a propagation phase is triggered in order to detect possible inconsistencies and reduce the search space. If this phase detects an inconsistency, the algorithm backtracks and removes the effects of the previous decisions. If no inconsistency is detected, a branching process is applied recursively to the child nodes until a solution is found or until all the search space has been explored.
The way the branching is done is defined by branching schemes (type cpbranching). Six branching schemes are predefined in Xpress Kalis:
- assign_var
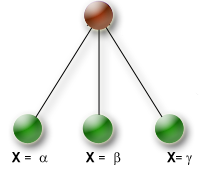
This branching scheme may be considered as the standard enumeration scheme in finite domain Constraint Programming. For a given branching variable it enumerates all values currently in its domain. A branch is formed by assigning a value to the branching variable, resulting in a variable number of branches per node (determined by the variable's domain size). Since this strategy tends to create a very wide search tree it is used preferably with small domains or if variable and value selection strategies are known that quickly lead to (good) feasible solutions.
- assign_and_forbid
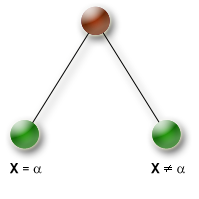
This branching scheme creates a binary search tree by creating two branches for a given branching variable. The first branch is formed by assigning a value to the branching variable, and the second branch, by forbidding this value for this variable.
- split_domain
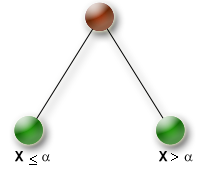
The split_domain strategy creates a binary search tree by splitting the domain of the branching variable into two intervals (all values less than or equal to the branching value in the first and all values greater than the branching value in the second). This strategy is the only possible choice for continuous variables and it is also applicable for finite domain variables. For the latter this strategy may be helpful if the initial domain sizes are relatively large. The strategy can be configured by choosing which branch to explore first and whether to stop applying it when domain sizes are reduced to less than a certain limit.
- probe_assign_var
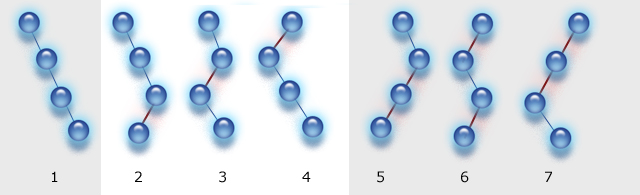
The probe_assign_var strategy is directly derived from the assign_var strategy which means that the branches created are the same. The difference lies in the completeness and the order in which branches are explored. Some of the possible branches are skipped by limiting the global number of times that the heuristic (first branch created) may fail and the branching process is stopped when this counter exceeds a specified value. The picture below shows the order in which the branches are explored when the domains of all variables are reduced to two values. This strategy can be useful to apply local search to an already known solution (combined with the KALIS_NEAREST_VALUE value selection heuristic) or to explore the neighborhood of a heuristic solution to find quickly a first solution and avoid the thrashing behavior of the chronological backtracking algorithm used during the resolution process.
- settle_disjunction
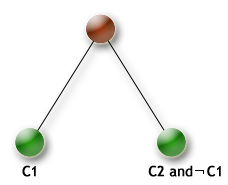
The settle_disjunction strategy creates a binary search tree by branching on the two possibilities defined by a disjunction. Recall that a disjunction can be written as c1 or c2 where c1 and c2 are two constraints, the settle_disjunction strategy will create a branch for each constraint stating that it must hold. The strategy can be configured by choosing the first branch of the disjunction that will be explored during the search process.
- probe_settle_disjunction

The probe_assign_var strategy is directly derived from the settle_disjunction strategy which means that the branches created by this strategy are the same. The difference lies in the completeness and the order in which branches are explored. Some of the possible branches are skipped by limiting the total number of times that the heuristic (first branch created) may fail and the branching process is stopped when this counter exceeds a specified value. The picture below shows the order in which the branches are explored when the domains of all variables are reduced to two values. This strategy can be useful to apply local search to a disjunctive scheduling problem for which a solution is already known (combined with the setfirstbranch and getactivebranch methods).
These predefined branching schemes are used in conjunction with variable (resp. disjunction) and value selection heuristics that fully define the way how the search tree will be explored.
Xpress Kalis predefines several variable selection heuristics:
- KALIS_SMALLEST_DOMAIN
- KALIS_MAX_DEGREE
- KALIS_SDOMDEG_RATIO
- KALIS_SMALLEST_MAX
- KALIS_SMALLEST_MIN
- KALIS_LARGEST_MAX
- KALIS_LARGEST_MIN
- KALIS_MAXREGRET_UB
- KALIS_MAXREGRET_LB
- KALIS_INPUT_ORDER
- KALIS_WIDEST_DOMAIN (continuous variables)
... value selection heuristics:
... and disjunction selection heuristics:
Xpress Kalis offers several possibilities to define the search strategy:
- Use the predefined strategy provided by Xpress Kalis.
- Build custom search strategies based on combinations of predefined branching schemes, variable and value selection heuristics.
- Define custom heuristics for variable and value selection.
- Add an optimization function (cost or objective function) for an enumeration and thus search for a feasible solution with the best (minimum or maximum) cost (optimal solution). We refer to this case as optimization, although, in practical applications one is typically only interested in good solutions that are found quickly, without necessarily spending time in proving that, indeed, the best solution is found.
The following example shows a specific problem and branching strategy with the corresponding search tree:
declarations
x : cpvar
y : cpvar
strategy : array(1..2) of cpbranching
end-declarations
1 <= x; x <= 3
1 <= y; y <= 3
strategy(1) := split_domain(KALIS_SMALLEST_DOMAIN, KALIS_MIN_TO_MAX, {x})
strategy(2) := assign_var(KALIS_SMALLEST_DOMAIN, KALIS_MIN_TO_MAX, {y})
cp_set_branching(strategy)
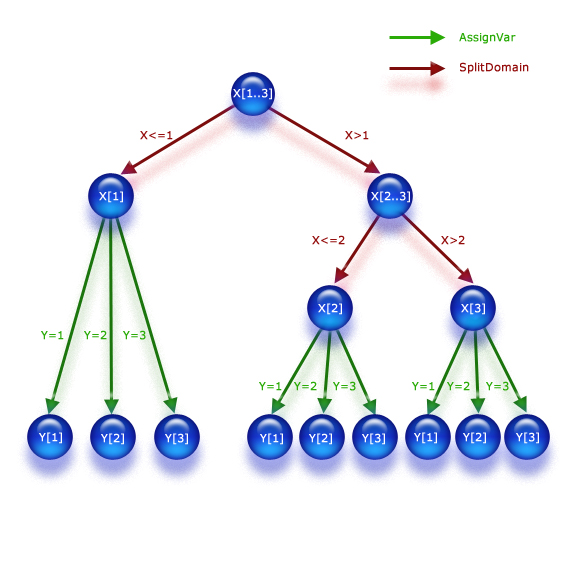
Figure 4.1: Example of search tree
| assign_and_forbid |
assign_and_forbid branching scheme
|
| assign_var |
assign_var branching scheme
|
| bs_group |
Create a group of branching schemes
|
| cp_set_branching |
Sets the strategy to use during the search for a solution
|
| cp_show_stats |
Shows some statistics about the search
|
| gettag |
Gets the tag of a constraint
|
| group_serializer |
Creates a branching scheme Group Serializer
|
| probe_assign_var |
probe_assign_var branching scheme
|
| probe_settle_disjunction |
probe_settle_disjunction branching scheme
|
| settle_disjunction |
settle_disjunction branching scheme
|
| split_domain |
split_domain branching scheme
|
| task_serialize |
task_serialize branching scheme
|
© 2001-2020 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

