Generic binary constraints: Euler knight tour
Our task is to find a tour on a chessboard for a knight figure such that the knight moves through every cell exactly once and at the end of the tour returns to its starting point. The path of the knight must follow the standard chess rules: a knight moves either one cell vertically and two cells horizontally, or two cells in the vertical and one cell in the horizontal direction, as shown in the following graphic (Figure Permissible moves for a knight):
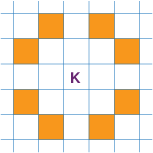
Figure 3.3: Permissible moves for a knight
Model formulation
To represent the chessboard we number the cells from 0 to N-1, where N is the number of cells of the board. The path of the knight is defined by N variables posi that indicate the ith position of the knight on its tour.
The first variable is fixed to zero as the start of the tour. Another obvious constraint we need to state is that all variables posi take different values (every cell of the chessboard is visited exactly once):
We are now left with the necessity to establish a constraint relation that checks whether consecutive positions define a valid knight move. To this aim we define a new binary constraint 'valid_knight_move' that checks whether a given pair of values defines a permissible move according to the chess rules for knight moves. Vertically and horizontally, the two values must be no more than two cells apart and the sum of the vertical and horizontal difference must be equal to three. The complete model then looks as follows.
pos1 = 0
all-different(pos1,...,posN)
∀i ∈ POS={1,...,N-1}: valid_knight_move(posi,posi+1)
valid_knight_move(posN,pos1)
Implementation
Testing whether moving from position a to position b is a valid move for a knight figure can be done with the following function valid_knight_move where 'div' means integer division without rest and 'mod' is the rest of the integer division:
| function valid_knight_move(a,b) xa := a div E ya := a mod E xb := b div E yb := b mod E deltax := |xa-xb| deltay := |ya-yb| return ((deltax ≤ 2) and (deltay ≤ 2) and (deltax + deltay = 3)) end-function |
The following Mosel model defines the user constraint function valid_knight_move as the implementation of the new binary constraints on pairs of movep variables (the constraints are established with generic_binary_constraint).
model "Euler Knight Moves"
uses "kalis"
parameters
S = 8 ! Number of rows/columns
NBSOL = 1 ! Number of solutions sought
end-parameters
forward procedure print_solution(sol: integer)
forward public function valid_knight_move(a:integer, b:integer): boolean
N:= S * S ! Total number of cells
setparam("KALIS_DEFAULT_LB", 0)
setparam("KALIS_DEFAULT_UB", N-1)
declarations
PATH = 1..N ! Cells on the chessboard
pos: array(PATH) of cpvar ! Cell at position p in the tour
end-declarations
! Fix the start position
pos(1) = 0
! Each cell is visited once
all_different(pos, KALIS_GEN_ARC_CONSISTENCY)
! The path of the knight obeys the chess rules for valid knight moves
forall(i in 1..N-1)
generic_binary_constraint(pos(i), pos(i+1), "valid_knight_move")
generic_binary_constraint(pos(N), pos(1), "valid_knight_move")
! Setting enumeration parameters
cp_set_branching(probe_assign_var(KALIS_SMALLEST_MIN, KALIS_MAX_TO_MIN,
pos, 14))
! Search for up to NBSOL solutions
solct:= 0
while (solct<NBSOL and cp_find_next_sol) do
solct+=1
cp_show_stats
print_solution(solct)
end-do
! **** Test whether the move from position a to b is admissible ****
public function valid_knight_move(a:integer, b:integer): boolean
declarations
xa,ya,xb,yb,delta_x,delta_y: integer
end-declarations
xa := a div S
ya := a mod S
xb := b div S
yb := b mod S
delta_x := abs(xa-xb)
delta_y := abs(ya-yb)
returned := (delta_x<=2) and (delta_y<=2) and (delta_x+delta_y=3)
end-function
!****************************************************************
! Solution printing
procedure print_solution(sol: integer)
writeln("Solution ", sol, ":")
forall(i in PATH)
write(getval(pos(i)), if(i mod 10 = 0, "\n ", ""), " -> ")
writeln("0")
end-procedure
end-model
The branching scheme used in this model is the probe_assign_var heuristic, in combination with the variable selection KALIS_SMALLEST_MIN (choose variable with smallest lower bound) and the value selection criterion KALIS_MAX_TO_MIN (from largest to smallest domain value). Another search strategy that was found to work well (though slower than the strategy in the code listing) is
cp_set_branching(assign_var(KALIS_SMALLEST_MIN, KALIS_MAX_TO_MIN, pos))
Our model defines two parameters. It is thus possible to change either the size of the chessboard (S) or the number of solutions sought (NBSOL) when executing the model without having to modify the model source.
Results
The first solution printed out by our model is the following tour.
0 -> 17 -> 34 -> 51 -> 36 -> 30 -> 47 -> 62 -> 45 -> 39 -> 54 -> 60 -> 43 -> 33 -> 48 -> 58 -> 52 -> 35 -> 41 -> 56 -> 50 -> 44 -> 38 -> 55 -> 61 -> 46 -> 63 -> 53 -> 59 -> 49 -> 32 -> 42 -> 57 -> 40 -> 25 -> 8 -> 2 -> 19 -> 4 -> 14 -> 31 -> 37 -> 22 -> 7 -> 13 -> 28 -> 18 -> 24 -> 9 -> 3 -> 20 -> 26 -> 16 -> 1 -> 11 -> 5 -> 15 -> 21 -> 6 -> 23 -> 29 -> 12 -> 27 -> 10 -> 0
Alternative implementation
Whereas the aim of the model above is to give an example of the definition of user constraints, it is possible to implement this problem in a more efficient way using the model developed for the cyclic scheduling problem in Section cycle: Paint production. The set of successors (domains of variables succp) can be calculated using the same algorithm that we have used above in the implementation of the user-defined binary constraints.
Without repeating the complete model definition at this place, we simply display the model formulation, including the calculation of the sets of possible successors (procedure calculate_successors, and the modified procedure print_sol for solution printout. We use a simpler version of the 'cycle' constraints than the one we have seen in Section cycle: Paint production, its only argument is the set of successor variables—there are no weights to the arcs in this problem.
model "Euler Knight Moves"
uses "kalis"
parameters
S = 8 ! Number of rows/columns
NBSOL = 1 ! Number of solutions sought
end-parameters
forward procedure calculate_successors(p: integer)
forward procedure print_solution(sol: integer)
N:= S * S ! Total number of cells
setparam("KALIS_DEFAULT_LB", 0)
setparam("KALIS_DEFAULT_UB", N)
declarations
PATH = 0..N-1 ! Cells on the chessboard
succ: array(PATH) of cpvar ! Successor of cell p
end-declarations
! Calculate set of possible successors
forall(p in PATH) calculate_successors(p)
! Each cell is visited once, no subtours
cycle(succ)
! Search for up to NBSOL solutions
solct:= 0
while (solct<NBSOL and cp_find_next_sol) do
solct+=1
cp_show_stats
print_solution(solct)
end-do
! **** Calculate possible successors ****
procedure calculate_successors(p: integer)
declarations
SuccSet: set of integer ! Set of successors
end-declarations
xp := p div S
yp := p mod S
forall(q in PATH) do
xq := q div S
yq := q mod S
delta_x := abs(xp-xq)
delta_y := abs(yp-yq)
if (delta_x<=2) and (delta_y<=2) and (delta_x+delta_y=3) then
SuccSet +={q}
end-if
end-do
setdomain(succ(p), SuccSet)
end-procedure
!****************************************************************
! **** Solution printing ****
procedure print_solution(sol: integer)
writeln("Solution ", sol, ":")
thispos:=0
nextpos:=getval(succ(0))
ct:=1
while (nextpos<>0) do
write(thispos, if(ct mod 10 = 0, "\n ", ""), " -> ")
val:=getval(succ(thispos))
thispos:=nextpos
nextpos:=getval(succ(thispos))
ct+=1
end-do
writeln("0")
end-procedure
end-model
The calculation of the domains for the succp variables reduces these to 2-8 elements (as compared to the N=64 values for every posp variables), which clearly reduces the search space for this problem.
This second model finds the first solution to the problem after 131 nodes taking just a fraction of a second to execute on a standard PC whereas the first model requires several thousand nodes and considerably longer running times. It is possible to reduce the number of branch-and-bound nodes even further by using yet another version of the 'cycle' constraint that works with successor and predecessor variables. This version of 'cycle' performs a larger amount of propagation, at the expense of (slightly) slower execution times for our problem. The procedure calculate_successors now sets the domain of predp to the same values as succp for all cells p.
declarations PATH = 0..N-1 ! Cells on the chessboard succ: array(PATH) of cpvar ! Successor of cell p pred: array(PATH) of cpvar ! Predecessor of cell p end-declarations ! Calculate sets of possible successors and predecessors forall(p in PATH) calculate_successors(p) ! Each cell is visited once, no subtours cycle(succ, pred)
Figure Knight's tour solution graph shows the graphical display of a knight's tour created with the user graph drawing functionality.
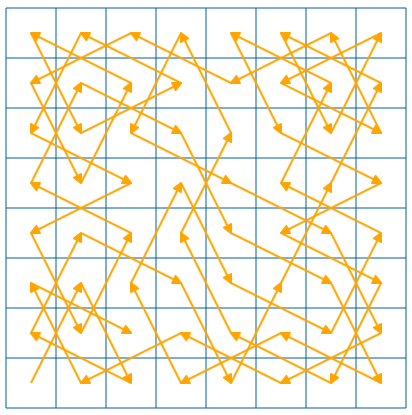
Figure 3.4: Knight's tour solution graph
Alternative implementation 2
Yet more efficient (a similar number of nodes with significantly shorter running times) is the following model version using the 'cycle' constraint described in Section cycle: Paint production. Since travel times from one position to the next are irrelevant in this model we simply fix all coefficients for the 'cycle' constraint to a constant and constrain the cycle length to the corresponding value.
All else, including the calculation of the sets of possible successors (procedure calculate_successors, and the procedure print_sol for solution printout is copied unchanged from the previous model.
model "Euler Knight Moves"
uses "kalis"
parameters
S = 8 ! Number of rows/columns
NBSOL = 1 ! Number of solutions sought
end-parameters
forward procedure calculate_successors(p: integer)
forward procedure print_solution(sol: integer)
N:= S * S ! Total number of cells
setparam("KALIS_DEFAULT_LB", 0)
setparam("KALIS_DEFAULT_UB", N)
declarations
PATH = 0..N-1 ! Cells on the chessboard
succ: array(PATH) of cpvar ! Successor of cell p
end-declarations
! Calculate set of possible successors
forall(p in PATH) calculate_successors(p)
! Each cell is visited once, no subtours
cycle(succ)
! Search for up to NBSOL solutions
solct:= 0
while (solct<NBSOL and cp_find_next_sol) do
solct+=1
cp_show_stats
print_solution(solct)
end-do
! **** Calculate possible successors ****
procedure calculate_successors(p: integer)
declarations
SuccSet: set of integer ! Set of successors
end-declarations
xp := p div S
yp := p mod S
forall(q in PATH) do
xq := q div S
yq := q mod S
delta_x := abs(xp-xq)
delta_y := abs(yp-yq)
if (delta_x<=2) and (delta_y<=2) and (delta_x+delta_y=3) then
SuccSet +={q}
end-if
end-do
setdomain(succ(p), SuccSet)
end-procedure
!****************************************************************
! **** Solution printing ****
procedure print_solution(sol: integer)
writeln("Solution ", sol, ":")
thispos:=0
nextpos:=getval(succ(0))
ct:=1
while (nextpos<>0) do
write(thispos, if(ct mod 10 = 0, "\n ", ""), " -> ")
val:=getval(succ(thispos))
thispos:=nextpos
nextpos:=getval(succ(thispos))
ct+=1
end-do
writeln("0")
end-procedure
end-model
© 2001-2020 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

