The duals of general, nonlinear program
The dual of a mathematical program plays a fundamental role in the theory of continuous optimization. Each variable in a problem has a corresponding partner in that problem's dual, and the values of those variables are called the reduced costs and dual multipliers (shadow prices). Xpress NonLinear makes estimates of these values available. These are normally defined in a similar way to the usual linear programming case, so that each value represents the rate of change of the objective when either increasing the corresponding primal variable or relaxing the corresponding primal constraint.
From an algorithmic perspective, one of the most important roles of the dual variables is to characterize local optimality. In this context, the dual multipliers and reduced costs are called Lagrange multipliers, and a solution with both primal and dual feasible variables satisfies the Karush-Kuhn-Tucker conditions. However, it is important to note that for general nonlinear problems, there exist situations in which there are no such multipliers. Geometrically, this means that the slope of the objective function is orthogonal to the linearization of the active constraints, but that their curvature still prevents any movement in the improving direction.
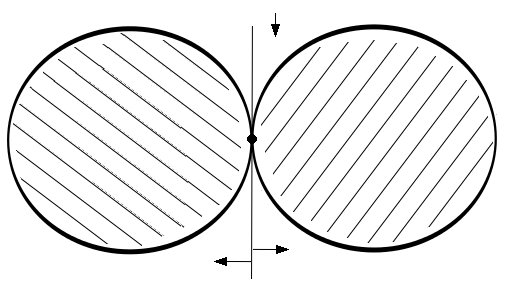
As a simple example, consider:| minimize | y |
| subject to | x2 + y2 ≤ 1 |
| (x-2)2 + y2 ≤ 1 |
Figure 7.3: A problem admitting no dual values
This problem has a single feasible solution at (1,0). Reduced costs and dual multipliers could never be meaningful indicators of optimality, and indeed are not well-defined for this problem. Intuitively, this arises because the feasible region lacks an interior, and the existence of an interior (also referred to as the Slater condition) is one of several alternative conditions which can be enforced to ensure that such situations do not occur. The other common condition for well-defined duals is that the gradients of the active constraints are linearly independent.
Problems without valid duals do not often arise in practice, but it is important to be aware of the possibility. Analytic detection of such issues is difficult, and they manifest instead in the form of unexpectedly large or otherwise implausible dual values.
© 2001-2020 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.