Implementation with Mosel
For the implementation (file folioheur.mos) of the variable fixing solution heuristic we work with the MIP 1 model from Chapter 6. Through the definition of the heuristic in the form of a subroutine (more precisely, a procedure) we only make minimal changes to the model itself: at the beginning we declare the procedure using the keyword forward, and before solving our problem with the standard call to the maximization function we execute our own solution heuristic. The solution printing also has been adapted.
model "Portfolio optimization solved heuristically"
uses "mmxprs" ! Use Xpress Optimizer
parameters
MAXRISK = 1/3 ! Max. investment into high-risk values
MAXVAL = 0.3 ! Max. investment per share
MINAM = 0.5 ! Min. investment into N.-American values
MAXNUM = 4 ! Max. number of assets
end-parameters
forward procedure solve_heur ! Heuristic solution procedure
declarations
SHARES: set of string ! Set of shares
RISK: set of string ! Set of high-risk values among shares
NA: set of string ! Set of shares issued in N.-America
RET: array(SHARES) of real ! Estimated return in investment
end-declarations
initializations from "folio.dat"
RISK RET NA
end-initializations
declarations
frac: array(SHARES) of mpvar ! Fraction of capital used per share
buy: array(SHARES) of mpvar ! 1 if asset is in portfolio, 0 otherwise
end-declarations
! Objective: total return
Return:= sum(s in SHARES) RET(s)*frac(s)
! Limit the percentage of high-risk values
sum(s in RISK) frac(s) <= MAXRISK
! Minimum amount of North-American values
sum(s in NA) frac(s) >= MINAM
! Spend all the capital
sum(s in SHARES) frac(s) = 1
! Upper bounds on the investment per share
forall(s in SHARES) frac(s) <= MAXVAL
! Limit the total number of assets
sum(s in SHARES) buy(s) <= MAXNUM
forall(s in SHARES) do
buy(s) is_binary
frac(s) <= buy(s)
end-do
! Solve problem heuristically
solve_heur
! Solve the problem
maximize(Return)
! Solution printing
if getprobstat=XPRS_OPT then
writeln("Exact solution: Total return: ", getobjval)
forall(s in SHARES) writeln(s, ": ", getsol(frac(s))*100, "%")
else
writeln("Heuristic solution is optimal.")
end-if
!-----------------------------------------------------------------
procedure solve_heur
declarations
TOL: real ! Solution feasibility tolerance
fsol: array(SHARES) of real ! Solution values for `frac' variables
bas: basis ! LP basis
end-declarations
setparam("XPRS_VERBOSE",true) ! Enable message printing in mmxprs
setparam("XPRS_CUTSTRATEGY",0) ! Disable automatic cuts
setparam("XPRS_HEURSTRATEGY",0) ! Disable automatic MIP heuristics
setparam("XPRS_PRESOLVE",0) ! Switch off presolve
TOL:=getparam("XPRS_FEASTOL") ! Get feasibility tolerance
setparam("ZEROTOL",TOL) ! Set comparison tolerance
maximize(XPRS_LPSTOP,Return) ! Solve the LP problem
savebasis(bas) ! Save the current basis
! Fix all variables `buy' for which `frac' is at 0 or at a relatively
! large value
forall(s in SHARES) do
fsol(s):= getsol(frac(s)) ! Get the solution values of `frac'
if (fsol(s) = 0) then
setub(buy(s), 0)
elif (fsol(s) >= 0.2) then
setlb(buy(s), 1)
end-if
end-do
maximize(XPRS_CONT,Return) ! Solve the MIP problem
ifgsol:=false
if getprobstat=XPRS_OPT then ! If an integer feas. solution was found
ifgsol:=true
solval:=getobjval ! Get the value of the best solution
writeln("Heuristic solution: Total return: ", solval)
forall(s in SHARES) writeln(s, ": ", getsol(frac(s))*100, "%")
end-if
! Reset variables to their original bounds
forall(s in SHARES)
if ((fsol(s) = 0) or (fsol(s) >= 0.2)) then
setlb(buy(s), 0)
setub(buy(s), 1)
end-if
loadbasis(bas) ! Load the saved basis
if ifgsol then ! Set cutoff to the best known solution
setparam("XPRS_MIPABSCUTOFF", solval+TOL)
end-if
end-procedure
end-model This model certainly requires some more detailed explanations.
Subroutines
A subroutine in Mosel has a similar structure as the model itself: a procedure starts with the keyword procedure, followed by the name of the procedure, and terminates with end-procedure. Similarly, a function starts with the keyword function, followed by its name, and terminates with end-function. Both types of subroutines may take a list of arguments and for functions in addition the return type must be indicated, for example:
function myfunc(myint: integer, myarray: array(range) of string): real
for a function that returns a real and takes as input arguments an integer and an array of string.
As shown in our example, a subroutine may contain one (or several) declarations blocks. The objects defined in a subroutine are only valid locally and are deleted at the end of the subroutine.
Subroutine definitions may be overloaded, that is, a single subroutine may take different combinations of arguments. It is possible to overload any subroutines defined by Mosel and its modules, provided that the new definition differs from the existing one(s) in at least one argument.
For more detail and further examples of subroutine definition see the `Mosel User Guide'.
Optimizer parameters and functions
Parameters: The solution heuristic starts with parameter settings for Xpress Optimizer. For a detailed explanation of all Optimizer parameters the reader is refered to the `Optimizer Reference Manual'. All parameters are accessed through the Mosel subroutines setparam and getparam. In the example, we first enable the output printing by the module mmxprs. As a result, more information than what is printed by our model will be displayed in the logging pane:
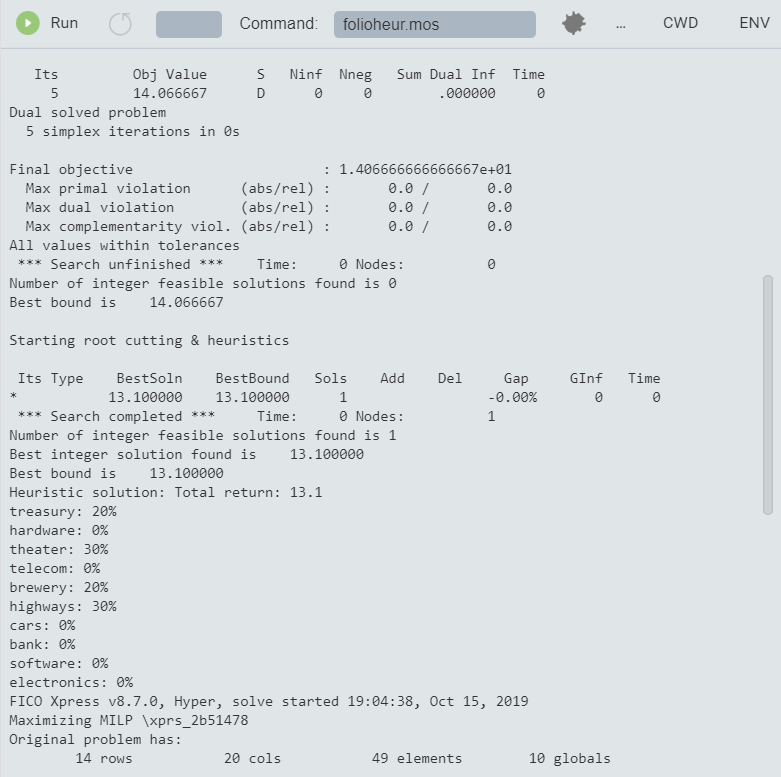
Figure 9.1: Optimizer output display
Switching off the automated cut generation (parameter XPRS_CUTSTRATEGY) and the MIP heuristics (parameter XPRS_HEURSTRATEGY) is optional, whereas it is required in our case to disable the presolve mechanism (a treatment of the matrix that tries to reduce its size and improve its numerical properties, set with parameter XPRS_PRESOLVE), because we interact with the problem in the Optimizer in the course of its solution and this is only possible correctly if the matrix has not been modified by the Optimizer.
In addition to the parameter settings we also retrieve the feasibility tolerance used by Xpress Optimizer: the Optimizer works with tolerance values for integer feasibility and solution feasibility that are typically of the order of 10-6 by default. When evaluating a solution, for instance by performing comparisons, it is important to take into account these tolerances.
Optimization statement: We use a new version of the maximization procedure with an additional argument, XPRS_LPSTOP, indicating that we only want to solve the top node LP relaxation (and not yet the entire MIP problem). To continue with MIP solving from the point where we have stopped the algorithm we use the argument XPRS_CONT. This is an example of an overloaded subroutine definition.
Saving and loading bases: To speed up the solution process, we save (in memory) the current basis of the Simplex algorithm after solving the initial LP relaxation, before making any changes to the problem. This basis is loaded again at the end, once we have restored the original problem. The MIP solution algorithm then does not have to re-solve the LP problem from scratch, it resumes the state where it was `interrupted' by our heuristic.
Bound changes: When a problem has already been loaded into the Optimizer (e.g. after executing an optimization statement or following an explicit call to loadprob) bound changes via setlb and setub are passed on directly to the Optimizer. Any other changes (addition or deletion of constraints or variables) always lead to a complete reloading of the problem.
For more detail on the Optimizer functionality used in this example see the documentation of the module mmxprs in the `Mosel Language Reference Manual'.
Comparison tolerance
After retrieving the feasibility tolerance of the Optimizer we set the comparison tolerance of Mosel (ZEROTOL) to this value TOL. This means that the test fsol(s) = 0 evaluates to true if fsol(s) lies between -TOL and TOL, and fsol(s) >= 0.2 is satisfied if the value of fsol(s) is at least 0.2-TOL.
Comparisons in Mosel always use a tolerance, with a very small default value. By resetting this parameter to the Optimizer feasibility tolerance Mosel evaluates solution values just like the Optimizer.

