Price breaks
All items discount: when buying a certain number of items we get discounts on all items that we buy if the quantity we buy lies in certain price bands.
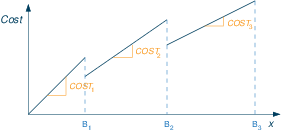
| less than B1 | COST1 each |
| ≥ B1 and < B2 | COST2 each |
| ≥ B2 and < B3 | COST3 each |
Formulation with binary variables or Special Ordered Sets of type 1 (SOS1):
- Define binary variables bi (i=1,2,3), where bi is 1 if we pay a unit cost of COSTi.
- Real decision variables xpi represent the number of items bought at price COSTi.
- The quantity bought is given by x= ∑ixpi , with a total price of ∑iCOSTi·xpi
- MIP formulation :
where the variables bi are either defined as binaries, or they form a Special Ordered Set of type 1 (SOS1), where the order is given by the values of the breakpoints Bi.∑i bi = 1 xp1 ≤ B1· b1 Bi-1· bi ≤ xpi ≤ Bi· bi for i=2,3
Formulation as piecewise linear expression:
- Specification as list of piecewise linear segments with associated intervals:
Implementation with Mosel:⋃i=1,2,3 [Bi-1,Bi[ : COSTi·x TotalCost:= pwlin(union(i in 1..3) [pws(B(i-1), COST(i)*x)])
- Specification as list of points:
Implementation with Mosel:⋃i=1,2,3 [Bi-1,COSTi·Bi-1,Bi,COSTi·Bi] TotalCost:= pwlin(x, union(i in 1..3) [B(i-1), COST(i)*B(i-1), B(i), COST(i)*B(i)])
Incremental pricebreaks: when buying a certain number of items we get discounts incrementally. The unit cost for items between 0 and B1 is COST1, items between B1 and B2 cost COST2 each, etc.
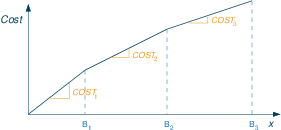
Formulation with Special Ordered Sets of type 2 (SOS2):
- Associate real valued decision variables wi (i=0,1,2,3) with the quantity break points B0 = 0, B1, B2 and B3.
- Cost break points CBPi (=total cost of buying quantity Bi):
CBP0=0 CBPi = CBPi-1+COSTi· (Bi-Bi-1) for i=1,2,3 - Constraint formulation:
where the wi form a SOS2 with reference row coefficients given by the coefficients in the definition of the total amount x.∑iwi=1 TotalCost = ∑i CBPi· wi x = ∑i Bi· wi
For a solution to be valid, at most two of the wi can be non-zero, and if there are two non-zero they must be contiguous, thus defining one of the line segments. - Implementation with Mosel (is_sos2 cannot be used here due to the 0-valued coefficient of w0):
Defx := x = sum(i in 1..3) B(i)*w(i) makesos2(My_Set, union(i in 0..3) {w(i)}, Defx)
Formulation using binaries:
- Define binary variables bi (i=1,2,3), where bi is 1 if we have bought any items at a unit cost of COSTi.
- Real decision variables xpi (i=1,..3) for the number of items bought at price COSTi.
- Total amount bought: x = ∑i xpi
- Constraint formulation:
(Bi-Bi-1)\cdot bi+1 ≤ xpi ≤ (Bi-Bi-1)\cdot bi for i=1,2 xp3 ≤ (B3-B2)\cdot b3 b1 ≥ b2 ≥ b3
Formulation as piecewise linear expression:
- Specification as list of slopes with associated intervals:
Implementation with Mosel (only points of slope changes are specified, start value is 0):⋃i=1,2,3 [Bi-1,Bi[ : COSTi TotalCost:= pwlin(x, union(i in 1..2) [B(i)], union(i in 1..3) [COST(i)])
- Specification as list of piecewise linear segments with associated intervals:
Implementation with Mosel:⋃i=1,2,3 [Bi-1,Bi[ : CBPi-1+COSTi·(x-Bi-1) TotalCost:= pwlin(union(i in 1..3) [pws(B(i), CBP(i,1)+COST(i)*(x-B(i-1)))])
- Specification as list of points:
Implementation with Mosel:⋃i=0,1,2,3 [Bi,CBPi] TotalCost:= pwlin(x, union(i in 0..3) [B(i), CBP(i)])

