Initializing help system before first use

Purchasing with price breaks

There are three suppliers of a good, and they have quoted various prices for various quantities of product. We want to buy at least total cost, yet not buy too much from any one supplier. Each supplier offers decreasing prices for increased lot size, in the form of incremental discounts (the data is given in Table Price profile). We wish to buy 600 items in total.

Table 5.1: Price profile
Supplier Unit price 1 Breakpoint 1 Unit price 2 Breakpoint 2 Unit price 3 Breakpoint 3
1 9.2 100 9 200 7 1000
2 9 50 8.5 250 8.3 2000
3 11 100 8.5 300 7.5 4000

For example, if you buy 150 items from supplier 1, you pay 9.2· 100+9· 50. If you buy 225 items from supplier 1, you pay 9.2· 100+9· 100+7· 25.

Model formulation

We write SUPPL for the set of suppliers, BREAK0 for the set of breakpoints including 0, and BREAK1 the set of breakpoints starting with the first point where unit cost changes, that is without 0. For every supplier s, Bsb (b ∈ BREAK1) denotes the breakpoint where the unit cost changes from COSTsb to COSTs,b+1; Bs0 is always 0. Furthermore REQ denotes the total amount we wish to buy, and MAXPERCs the maximum percentage that may be bought from supplier s.

MoselUG/pricebrincug

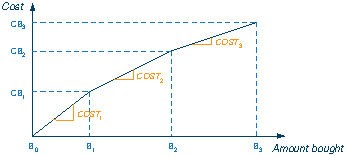
Figure 5.1: Price curve of a supplier

To formulate this problem, we introduce two sets of variables. buys represents the quantity bought from supplier s. These quantities are calculated via weight variables wsb associated with the breakpoints. The weight variables for every supplier s form an SOS-2 (Special Ordered Set of Type 2), that means that at most two neighboring variables wsb in the order induced by the coefficients BRbs may be non-zero. Under the condition that the weight variables sum up to 1 for every supplier we can use these variables to linearly interpolate between the breakpoints to obtain the quantities bought:

∀ s ∈ SUPPL: ∑b ∈ BREAK0 Bsb· wsb = buys
∀ s ∈ SUPPL: ∑b ∈ BREAK0 wsb = 1

Furthermore, we need to express the constraints that the total requirement must be met and that no more than a certain given percentage may be bought of each supplier.

∑s ∈ SUPPL buys ≥ REQ
∀ s ∈ SUPPL: buy(s) ≤ MAXPERCs/100·REQ

The total cost at the breakpoints, CBsb, is given by the following recursive formula:

CBs0 = 0
∀ b ∈ BREAK1: CBsb = CBs,b-1 + COSTsb· (Bsb-Bs,b-1)

With these total cost values per supplier we can formulate the objective function which is to minimize the total cost of the purchase.

minimize ∑s ∈ SUPPL∑b ∈ BREAK0 CBsb· wsb

Implementation

The Mosel implementation of the mathematical model looks as follows (file purch.mos). 

model "Purchase"
 uses "mmxprs"

 declarations
   NB = 3
   BREAK1 = 1..NB                     ! Price breaks
   BREAK0 = 0..NB                     ! Price breaks including 0
   SUPPL = 1..3                       ! Suppliers

   COST: array(SUPPL,BREAK1) of real  ! Unit cost
   B: array(SUPPL,BREAK0) of real     ! Breakpoints (quantities at which unit
                                      ! cost changes)
   CB: array(SUPPL,BREAK0) of real    ! Total cost at break points
   MAXPERC: array(SUPPL) of real      ! Maximum percentages for each supplier
   REQ: real                          ! Total quantity required

   buy: array(SUPPL) of mpvar         ! Quantity to purchase from supplier s
   w: array(SUPPL,BREAK0) of mpvar    ! Weights at breakpoint k for supplier s
 end-declarations

 initializations from 'purch.dat'
   COST B MAXPERC REQ
 end-initializations

! Calculate total cost at breakpoints
 forall(s in SUPPL) do
   CB(s,0):= 0
   forall(b in BREAK1) CB(s,b):= CB(s,b-1) + COST(s,b)*(B(s,b)-B(s,b-1))
 end-do

! Objective: sum of costs*weights
 MinCost:= sum(s in SUPPL, b in BREAK0) CB(s,b) * w(s,b)

! Define buy and also order the weight variables by breakpoint quantities
 forall(s in SUPPL) sum(b in BREAK0) B(s,b) * w(s,b) = buy(s)

! The convexity row (w sum to 1)
 forall(s in SUPPL) sum(b in BREAK0) w(s,b) = 1

! The minimum quantity that must be bought
 sum(s in SUPPL) buy(s) >= REQ

! No more than the maximum percentage from each supplier
 forall(s in SUPPL) buy(s) <= MAXPERC(s)*REQ/100.0

! Define the w as SOS-2
 forall(s in SUPPL)
   makesos2(union(b in BREAK0) {w(s,b)}, sum(b in BREAK0) B(s,b)*w(s,b))

 minimize(MinCost)              ! Solve the MIP-problem

 writeln("Minimum total cost: ", getobjval)
 forall(s in SUPPL) writeln(" buy(",s,"): ", getsol(buy(s)), " cost: ",
   getsol(sum(b in BREAK0) CB(s,b) * w(s,b)) )

end-model

In the model above we use the procedure makesos2 for the definition of the SOS-2. Alternatively, if we wish to use is_sos2, then the weight coefficients B(s,b) all need to be augmented by some non-zero constant EPS since Mosel does not accept 0-valued weights with is_sos2. 

forall(s in SUPPL) sum(b in BREAK0) (B(s,b)+EPS) * w(s,b) is_sos2

The minimum cost of €5,435 is obtained by buying 240 items from supplier 1, 210 from supplier 2, and 150 items from supplier 3.

Parent Topic Integer Programming