Example problem: jobshop scheduling

We wish to schedule the production of a set of jobs on a set of machines. Every job is produced by a sequence of tasks, each of these tasks is processed on a different machine with a specific given duration. A machine processes at most one job at a time. Tasks are non-preemptive (once started the processing cannot be interrupted). The objective is to minimize the total duration of the schedule, that is, the completion time of the last task, also referred to as makespan.

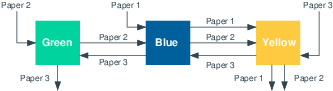
Figure 8: Jobshop example with 3 jobs (wallpapers) and 3 machines (colors)

This combinatorial problem is notoriously difficult to solve to optimality with mathematical programming approaches even for relatively small data instances. For practical purposes it is therefore quite a common practice to work with heuristics or some form of incomplete search, for example by stopping the solution algorithms after a certain laps of time. In such a case it is particularly important to be able to quickly compute good solutions and lower bound estimates.

Our start solution heuristic for the jobshop problem relies on the following idea: By solving single machine subproblems (sequencing the tasks that are processed on the same machine) we can generate partial solutions to the full jobshop problem that are loaded as start solutions into the MIP optimizer. This approach requires us to state and solve two distinct problems:

Several instances (one per machine) of a sequencing problem—these subproblems are independent and can therefore be formulated and solved concurrently
One instance of the full jobshop problem

Jobshop scheduling model

For the formulation of the jobshop problem we work with a set of JOBS, each composed of a series of TASKS that represent the processing of a job j on a specific resource m (from the set RESOURECS) with a known duration DUR_jm. The decision variables are the start and completion times of the tasks (start_jt and comp_jt respectively) and a set of binary variables y_mij for stating the sequence of tasks from two different jobs i and j on a resource m.

The objective function variable makespan is constrained to take the value of the latest completion time. We further need to state the order of tasks within every job (precedence relations) and the sequence of tasks on a given resouces (disjunctions between tasks).

Objective:

minimize makespan

Decision variables:

∀ j ∈ JOBS, t ∈ TASKS: start_jt,comp_jt ∈ [0,MAXTIME]
∀ m ∈ RESOURCES, i<j ∈ JOBS: y_mij ∈ {0,1}

Precedence relations:

∀ j ∈ JOBS: makespan ≥ start_j,NBRES + DUR_j,NBRES
∀ j ∈ JOBS, t ∈ TASKS-{NBRES}: start_jt + DUR_jt ≤ start_j,t+1

Disjunctions between tasks on same machine:

∀ m ∈ RESOURCES, i<j ∈ JOBS: start_{i,RES_mi} +DUR_{i,RES_mi} ≤ start_{j,RES_mj} + M·y_mij
start_{j,RES_mj} +DUR_{j,RES_mj} ≤ start_{i,RES_mi} + M·(1-y_mij)

Linking start and completion times:

∀ j ∈ JOBS, t ∈ TASKS: start_jt + DUR_jt = comp_jt

Single machine sequencing subproblem

The sequencing problem on a specific machine m is expressed via a separate set of binary decision variables rank_jk that indicate whether the task from job j is processed in position k on this resource. The start time of the task in position k is expressed by tstart_k. We take into account the release date REL_j (sum of the durations of preceding tasks) and the total duration (processing time DUR_jm of the task itself and duration DURSUCC_j of all its successors within the job) for calculating a job completion time jcomp_j, the maximum of which (= makespan) is to be minimized. This makespan of the individual subproblems provides a lower bound on the makespan of the full jobshop problem.

Objective:

minimize makespan

Decision variables:

∀ j,k ∈ JOBS: rank_jk ∈ {0,1}
∀ j ∈ JOBS: jcomp_j ∈ [0,MAXTIME]
∀ k ∈ JOBS: tstart_k ∈ [0,MAXTIME]

One job per position, one position per job:

∀ k ∈ JOBS: ∑_{j ∈ JOBS} rank_jk = 1
∀ j ∈ JOBS: ∑_{k ∈ JOBS} rank_jk = 1

Sequence of jobs:

∀ k ∈ 1,...,NJOBS-1: tstart_k+1 ≥ tstart_k + ∑_{j ∈ JOBS} DUR_jm·rank_jk

Release dates for start times:

∀ k ∈ JOBS: tstart_k ≥ ∑_{j ∈ JOBS} REL_j·rank_jk

Completion times:

∀ k ∈ JOBS: jcomp_k = tstart_k + ∑_{j ∈ JOBS} (DUR_jm+DURSUCC_j)·rank_jk
makespan ≥ jcomp_k

Contents

Index

Glossary

Search Results

Example problem: jobshop scheduling

Jobshop scheduling model

Single machine sequencing subproblem