Disjunctive scheduling: unary resources

The problem of sequencing jobs on a single machine described in Section element: Sequencing jobs on a single machine may be represented as a disjunctive scheduling problem using the `task' and `resource' modeling objects.

The reader is reminded that the problem is to schedule the processing of a set of non-preemptive tasks (or jobs) on a single machine. For every task j its release date, duration, and due date are given. The problem is to be solved with three different objectives, minimizing the makespan, the average completion time, or the total tardiness.

Model formulation

The major part of the model formulation consists of the definition of the scheduling objects `tasks' and `resources'.

Every job j (j ∈ JOBS = {1,...,NJ}) is represented by a task object task_j, with a start time task_j.start in {REL_j,...,MAXTIME} (where MAXTIME is a sufficiently large value, such as the sum of all release dates and all durations, and REL_j the release date of job j) and the task duration task_j.duration fixed to the given processing time DUR_j. All jobs use the same resource res of unitary capacity. This means that at most one job may be processed at any one time, we thus implicitly state the disjunctions between the jobs.

Another implicit constraint established by the task objects is the relation between the start, duration, and completion time of a job j.

Objective 1: The first objective is to minimize the makespan (completion time of the schedule) or, equivalently, to minimize the completion time finish of the last job. The complete model is then given by the following (where MAXTIME is a sufficiently large value, such as the sum of all release dates and all durations):

Objective 2: The formulation of the second objective (minimizing the average processing time or, equivalently, minimizing the sum of the job completion times) remains unchanged from the first model—we introduce an additional variable totComp representing the sum of the completion times of all jobs.

Objective 3: To formulate the objective of minimizing the total tardiness, we introduce new variables late_j to measure the amount of time that a job finishes after its due date. The value of these variables corresponds to the difference between the completion time of a job j and its due date DUE_j. If the job finishes before its due date, the value must be zero. The objective now is to minimize the sum of these tardiness variables:

Implementation

The following implementation with Xpress Kalis (file b4seq3_ka.mos) shows how to set up the necessary task and resource modeling objects. The resource capacity is set with procedure set_resource_attributes (the resource is of the type KALIS_UNARY_RESOURCE meaning that it processes at most one task at a time), for the tasks we use the procedure set_task_attributes. The latter exists in several overloaded versions for different combinations of arguments (task attributes)—the reader is referred to the Xpress Kalis Reference Manual for further detail.

For the formulation of the maximum constraint we use an (auxiliary) list of variables: Xpress Kalis does not allow the user to employ the access functions to modeling objects (getstart, getduration, etc.) in set expressions such as union(j in JOBS) {getend(task(j))}.

model "B-4 Sequencing (CP)"
 uses "kalis"

 forward procedure print_sol
 forward procedure print_sol3

 declarations
  NJ = 7                          ! Number of jobs
  JOBS=1..NJ

  REL: array(JOBS) of integer     ! Release dates of jobs
  DUR: array(JOBS) of integer     ! Durations of jobs
  DUE: array(JOBS) of integer     ! Due dates of jobs

  task: array(JOBS) of cptask     ! Tasks (jobs to be scheduled)
  res: cpresource                 ! Resource (machine)

  finish: cpvar                   ! Completion time of the entire schedule
 end-declarations

 initializations from 'Data/b4seq.dat'
  DUR REL DUE
 end-initializations

! Setting up the resource (formulation of the disjunction of tasks)
 set_resource_attributes(res, KALIS_UNARY_RESOURCE, 1)

! Setting up the tasks (durations and disjunctions)
 forall(j in JOBS) set_task_attributes(task(j), DUR(j), res)

 MAXTIME:= max(j in JOBS) REL(j) + sum(j in JOBS) DUR(j)

 forall(j in JOBS) do
  0 <= getstart(task(j)); getstart(task(j)) <= MAXTIME
  0 <= getend(task(j)); getend(task(j)) <= MAXTIME
 end-do

! Start times
 forall(j in JOBS) getstart(task(j)) >= REL(j)

!**** Objective function 1: minimize latest completion time ****
 declarations
  L: cpvarlist
 end-declarations

 forall(j in JOBS) L += getend(task(j))
 finish = maximum(L)

 if cp_schedule(finish) >0 then
  print_sol
 end-if


!**** Objective function 2: minimize average completion time ****
 declarations
  totComp: cpvar
 end-declarations

 totComp = sum(j in JOBS) getend(task(j))

 if cp_schedule(totComp) > 0 then
  print_sol
 end-if


!**** Objective function 3: minimize total tardiness ****
 declarations
  late: array(JOBS) of cpvar      ! Lateness of jobs
  totLate: cpvar
 end-declarations

 forall(j in JOBS) do
  0 <= late(j); late(j) <= MAXTIME
 end-do

! Late jobs: completion time exceeds the due date
 forall(j in JOBS) late(j) >= getend(task(j)) - DUE(j)

 totLate = sum(j in JOBS) late(j)
 if cp_schedule(totLate) > 0 then
  writeln("Tardiness: ", getsol(totLate))
  print_sol
  print_sol3
 end-if


!-----------------------------------------------------------------

! Solution printing
 procedure print_sol
  writeln("Completion time: ", getsol(finish) ,
          "  average: ", getsol(sum(j in JOBS) getend(task(j))))
  write("Rel\t")
  forall(j in JOBS) write(strfmt(REL(j),4))
  write("\nDur\t")
  forall(j in JOBS) write(strfmt(DUR(j),4))
  write("\nStart\t")
  forall(j in JOBS) write(strfmt(getsol(getstart(task(j))),4))
  write("\nEnd\t")
  forall(j in JOBS) write(strfmt(getsol(getend(task(j))),4))
  writeln
 end-procedure

 procedure print_sol3
  write("Due\t")
  forall(j in JOBS) write(strfmt(DUE(j),4))
  write("\nLate\t")
  forall(j in JOBS) write(strfmt(getsol(late(j)),4))
  writeln
 end-procedure

end-model

Results

This model produces similar results as those reported for the model versions in Section element: Sequencing jobs on a single machine. Figure Solution Gantt chart shows a Gantt chart display of the solution. Above the Gantt chart we can see the resource usage display: the machine is used without interruption by the tasks, that is, even if we relaxed the constraints given by the release times and due dates it would not have been possible to generate a schedule terminating earlier.

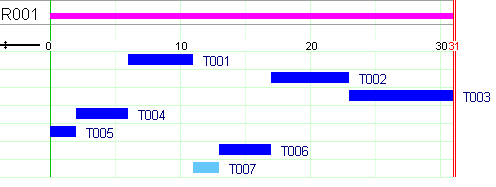
Figure 5.1: Solution Gantt chart