Mathematical Programming

Mathematical Programming is a technique of mathematical optimization. Many real-world problems in such different areas as industrial production, transport, telecommunications, finance, or personnel planning may be cast into the form of a Mathematical Programming problem: a set of decision variables, constraints over these variables and an objective function to be maximized or minimized.

Mathematical Programming problems are usually classified according to the types of the decision variables, constraints, and the objective function.

A well-understood case for which efficient algorithms (Simplex, interior point) are known comprises Linear Programming (LP) problems. In this type of problem all constraints and the objective function are linear expressions of the decision variables, and the variables have continuous domains—i.e., they can take on any, usually non-negative, real values. Luckily, many application problems fit into this category. Problems with hundreds of thousands, or even millions of variables and constraints are routinely solved with commercial Mathematical Programming software like Xpress Optimizer.

Researchers and practitioners working on LP quickly found that continuous variables are insufficient to represent decisions of a discrete nature (`yes'/`no' or 1,2,3,...). This observation lead to the development of Mixed Integer Programming (MIP) where constraints and objective function are linear just as in LP and variables may have either discrete or continuous domains. To solve this type of problems, LP techniques are coupled with an enumeration (known as Branch-and-Bound) of the feasible values of the discrete variables. Such enumerative methods may lead to a computational explosion, even for relatively small problem instances, so that it is not always realistic to solve MIP problems to optimality. However, in recent years, continuously increasing computer speed and even more importantly, significant algorithmic improvements (e.g. cutting plane techniques and specialized branching schemes) have made it possible to tackle ever larger problems, modeling ever more exactly the underlying real-world situations.

Another class of problems that is relatively well-handled are Quadratic Programming (QP) problems: these differ from LPs in that they have quadratic terms in the objective function (the constraints remain linear). The decision variables may be continuous or discrete, in the latter case we speak of Mixed Integer Quadratic Programming (MIQP) problems. In Chapters 7 and 12 of this book we show examples of both cases.

More difficult is the case of non-linear constraints or objective functions, Non-linear Programming (NLP) problems. Heuristic or approximation methods are employed to find good (locally optimal) solutions. Methods for solving non-linear problems to local optimality are Successive Linear Programming (SLP) and interior point methods. Such solvers form Xpress Nonlinear—a part of the FICO Xpress Optimization suite. If one desires to solve non-linear and mixed-integer non-linear problems to global optimality, FICO Xpress Global provides that functionality. Combined with Xpress Optimizer, FICO Xpress Nonlinear and Global can solve mixed-integer non-linear programming problems (MINLPs). However, in this book we shall not enlarge on this topic.

Building a model, solving it and then implementing the `answers' is not generally a linear process. We often make mistakes in our modeling which are usually only detected by the optimization process, where we could get answers that were patently wrong (e.g. unbounded or infeasible) or that do not accord with our intuition. If this happens we are forced to reflect further about the model and go into an iterative process of model refinement, re-solution and further analyses of the optimum solution. During this process it is quite likely that we will add extra constraints, perhaps remove constraints that we were mislead into adding, correct erroneous data or even be forced to collect new data that we had previously not considered necessary.

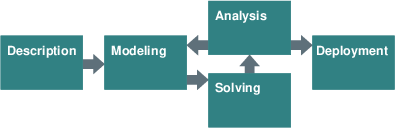
Figure 2.1: Scheme of an optimization project

This books takes the reader through all these steps: from the textual description we develop a mathematical model which is then implemented and solved. Various improvements, additions and reformulations are suggested in the following chapters, including an introduction of the available means to support the analysis of the results. The deployment of a Mathematical Programming application typically includes its embedding into other applications to turn it into a part of a company's information system.