Introduction
Topics covered in this chapter:
- Xpress Kalis Module for Mosel
- Software installation
- Basic concepts of Constraint Programming
- Contents of this document
Constraint Programming is an approach to problem solving that has been particularly successful for dealing with nonlinear constraint relations over discrete variables. In the following we therefore often use `Constraint Programming' or `CP' synonymously to `finite domain Constraint Programming'.
In the past, CP has been successfully applied to such different problem types as production scheduling (with or without resource constraints), sequencing and assignment of tasks, workforce planning and timetabling, frequency assignment, loading and cutting, and also graph coloring.
The strength of CP lies in its use of a high-level semantics for stating the constraints that preserves the original meaning of the constraint relations (such high-level constraints are referred to as global constraints). It is not necessary to translate constraints into an arithmetic form—a process whereby sometimes much of the problem structure is lost. The knowledge about a problem inherent to the constraints is exploited by the solution algorithms, rendering them more efficient.
Xpress Kalis Module for Mosel
The Xpress Kalis Module for Mosel, or short Kalis for Mosel, provides access to the FICO® Xpress Kalis Constraint Programming solver by Artelys from Mosel via the module kalis. Through the kalis module, the Constraint Programming functionality of Kalis becomes available in the Mosel environment, allowing the user to formulate and solve CP models in the Mosel language. Xpress Kalis combines a finite domain solver and a solver over continuous (floating point) variables. To aid the formulation of scheduling problems, the software defines specific aggregate modeling objects representing tasks and resources that will automatically setup certain (implicit) constraint relations and trigger the use of built-in search strategies specialized for this type of problem. Standard scheduling problems may thus be defined and solved simply by setting up the corresponding task and resource objects. Additionally, Xpress Kalis provides automatic linear relaxations of its constraints to ease the formulation and solving of a wide range of optimization problems.
All data handling facilities of the Mosel environment, including data transfer in memory (using the Mosel IO drivers) and ODBC access to databases (through the module mmodbc) can be used with kalis without any extra effort.
The Mosel language supports typical programming constructs, such as loops, subroutines, etc., that may be required to implement more complicated algorithms. Mosel can also be used as a platform for combining different solvers, in particular Xpress Kalis with Xpress Optimizer for joint CP – LP/MIP problem solving (See the Xpress Whitepapers Multiple models and parallel solving with Mosel and Hybrid MIP/CP solving with Xpress Optimizer and Xpress Kalis). This manual explains the basics on modeling and programming with Mosel and, where necessary, also some more advanced features. For a complete documentation and a more thorough introduction to its use the reader is referred to the Mosel Language Reference Manual and the Mosel User Guide.
Note on product versions
Most examples in this manual have originally been developed using the release 2007.1.0 of Xpress Kalis, their implementations have been updated to release 13.2 of Xpress Kalis with the Xpress Release 8.14 of Mosel (6.0). If they are run with other product versions the output obtained may look different. In particular, improvements to the algorithms in the CP solver or modifications to the default settings in Xpress Kalis may influence the behavior of the constraints or the search. Xpress Workbench screenshots have been updated to Xpress Release 8.7.
Software installation
To be able to work with Xpress Kalis, the Xpress Mosel software and Xpress Kalis must be installed and licensed. Users may find it convenient to install (in addition) the graphical environment Xpress Workbench for working with CP models, but this is not a prerequisite: Mosel models can be edited with any text editor and simply be executed from the command line. The examples of Chapter Hybridization of CP and MP of this manual can only be executed if Xpress Optimizer is also present and licensed.
Follow the installation instructions provided with the Xpress distribution for installing Mosel (and Xpress Workbench) and the required solvers on your computer by selecting the Xpress Kalis add-on option during the installation process.
Basic concepts of Constraint Programming
A Constraint Programming (CP) problem is defined by its decision variables with their domains and constraints over these variables. The problem definition is usually completed by a branching strategy (also referred to as enumeration or search strategy).
CP makes active use of the concept of variable domains, that is, the set out of which a decision variable takes its values. In finite domain Constraint Programming these are sets or intervals of integer numbers.
Each constraint in CP comes with its own (set of) solution algorithm(s), typically based on results from other areas, such as graph theory. Once a constraint has been established it maintains its set of variables in a solved state, i.e., its solution algorithm removes any values that it finds infeasible from the domains of the variables.
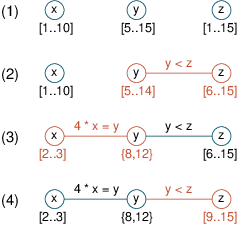
The constraints in a CP problem are linked by a mechanism called constraint propagation: whenever the domain of a variable is modified this triggers a re-evaluation of all constraints on this variable which in turn may cause modifications to other variables or further reduction of the domain of the first variable as shown in the example in Figure Example of constraint propagation, (a) finite domain (discrete) variables, (b) continuous variables. (the original domains of the variables are reduced by the addition of two constraints; in the last step the effect of the second constraint is propagated to the first constraint, triggering its re-evaluation).
| (a) | ||||
 |
 |
Figure 1.1: Example of constraint propagation, (a) finite domain (discrete) variables, (b) continuous variables.
A CP problem is built up incrementally by adding constraints and bounds on its variables. The solving of a CP problem starts with the statement of the first constraint—values that violate the constraint relation are removed from the domains of the involved variables. Since the effect of a newly added constraint is propagated immediately to the entire CP problem it is generally not possible to modify or delete this constraint from the problem later on.
In some cases the combination of constraint solving and the propagation mechanism may be sufficient to prove that a problem instance is infeasible, but most of the time it will be necessary to add an enumeration for reducing all variable domains to a single value (consistent instantiation or feasible solution) or proving that no such solution exists. In addition it is possible to define an objective function (or cost function) and search for a feasible solution with the best objective function value (optimal solution).
Contents of this document
This document gives an introduction to working with Xpress Kalis from Mosel. Basic notions of Constraint Programming are explained but it is expected that the reader has some general understanding of CP techniques. Since we are working with the kalis module for Xpress Mosel this document also describes features of the Mosel language where this appears neccessary to the understanding of the presented examples.
By the means of example models we illustrate the use of Xpress Kalis, presenting the new types that are defined by the kalis module, namely
- Decision variables: finite domain and floating point variables
- Constraints: absolute value and distance, all-different, element, generic binary, linear, maximum and minimum, occurrence, and logical relations
- Enumeration: predefined branching schemes and user search strategies
- Scheduling: aggregate modeling objects representing tasks and resources
The first chapter deals with the basics of writing CP models with Mosel. It explains the general structure of CP models and some basics on working with Mosel, including data handling. Then follows a series of small problems illustrating the use of the different constraint relation types in Xpress Kalis. The next chapter introduces in a more systematic way the different possibilities of defining enumeration strategies, some of which already appear in the preceding model examples. The chapter dedicated to the topic of scheduling introduces the modeling objects `task' and `resource' that simplify the formulation of scheduling problems. The following chapter familiarizes the reader with the concept of linear relaxations and shows how to work with them.
Apart from the initial examples, every example is presented as follows:
- Example description
- Formulation as a CP model
- Implementation with Mosel using the kalis module: code listing and explanations
- Results
All example models of this document are included with the set of examples that is provided as part of the Xpress Kalis distribution.
© 2001-2026 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

