Selecting the right algorithm for a nonlinear problem - when to use the XPRS library instead of XSLP
This chapter focuses on the nonlinear capabilities of the Xpress XPRS optimizer. As a general rule of thumb, problems that can be handled by the XPRS library do not require the use of XSLP; while Xpress XSLP is able to efficiently solve most nonlinear problems, there are subclasses of nonlinear problems for which the Xpress optimizer features specialized algorithms that are able to solve those problems more efficiently and in larger sizes. These are notably the convex quadratic programming and the convex quadratically constrained problems and their mixed integer counterparts.
It is also possible to separate the convex quadratic information from the rest of XSLP, and let the Xpress XPRS optimizer handle those directly. Doing so is good modelling practice, but emphasis must be placed on that the optimizer can only handle convex quadratic constraints.
Convex Quadratic Programs (QPs)
Convex Quadratic Programming (QP) problems are an extension of Linear Programming (LP) problems where the objective function may include a second order polynomial. The FICO Xpress Optimizer can be used directly for solving QP problems (and the Mixed Integer version MIQP).
If there are no other nonlinearities in the problem, the XPRS library povides specialized algorithms for the solution of convex QP (MIQP) problems, that are much more efficient than solving the problem as a general nonlinear problem with XSLP.
Convex Quadratically Constrained Quadratic Programs (QCQPs)
Quadratically Constrained Quadratic Programs (QCQPs) are an extension of the Quadratic Programming (QP) problem where the constraints may also include second order polynomials.
A QCQP problem may be written as:
| minimize: | c1x1+...+cnxn+xTQ0x | ||
| subject to: | a11x1+...+a1nxn+xTQ1x | ≤ | b1 |
| ... | |||
| am1x1+...+amnxn+xTQmx | ≤ | bm | |
| l1≤x1≤u1,...,ln≤xn≤un |
where any of the lower or upper bounds li or ui may be infinite.
If there are no other nonlinearities in the problem, the XPRS library povides specialized algorithms for the solution of convex QCQP (and the integer counterpart MIQCQP) problems, that are much more efficient than solving the problem as a general nonlinear problem with XSLP.
Convexity
A fundamental property for nonlinear optimization problems, thus in QCQP as well, is convexity. A region is called convex, if for any two points from the region the connecting line segment is also part of the region.
The lack of convexity may give rise to several unfavorable model properties. Lack of convexity in the objective may introduce the phenomenon of locally optimal solutions that are not global ones (a local optimal solution is one for which a neighborhood in the feasible region exists in which that solution is the best). While the lack of convexity in constraints can also give rise to local optimums, they may even introduce non–connected feasible regions as shown in Figure Non-connected feasible regions.
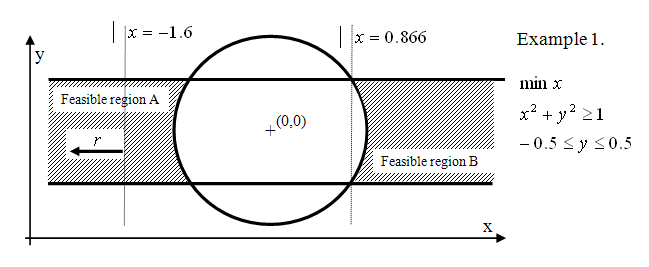
Figure 26.1: Non-connected feasible regions
In this example, the feasible region is divided into two parts. Over feasible region B, the objective function has two alterative local optimal solutions, while over feasible region A the objective is not even bounded.
For convex problems, each locally optimal solution is a global one, making the characterization of the optimal solution efficient.
Characterizing Convexity in Quadratic Constraints
A quadratic constraint of form
defines a convex region if and only if Q is a so–called positive semi–definite (PSD) matrix.
A rectangular matrix Q is PSD by definition, if for any vector (not restricted to the feasible set of a problem) x it holds that xTQx≥0.
It follows that for greater or equal constraints
the negative of Q shall be PSD.
A nontrivial quadratic equality constraint (one for which not every coefficient is zero) always defines a nonconvex region, therefore those must be modelled as XSLP structures.
There is no straightforward way of checking if a matrix is PSD or not. An intuitive way of checking this property, is that the quadratic part shall always only make a constraint harder to satisfy (i.e. taking the quadratic part away shall always be a relaxation of the original problem).
There are certain constructs however, that can easily be recognized as being non convex:
- the product of two variables say xy without having both x2 and y2 defined;
- having - x2 in any quadratic expression in a less or equal, or having x2 in any greater or equal row.
As a general rule, a convex quadratic objective and convex quadratic constraints are best handled by the XPRS library; while all nonconvex counterparts should be modelled as XSLP structures.

