produces
produces |
Purpose
Sets the minimal and maximal amount of resource produced by a task for a particular resource.
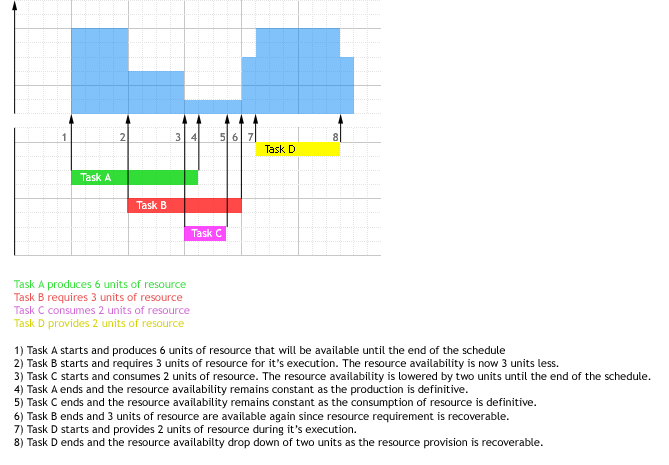
A task produces some amount of processing power for a resource at its start. The capacity produced is considered as non renewable which means that the produced capacity remains available even after the completion of the task. Note that a minimal amount of 0 is possible thus allowing modelisation of alternative resources. The type of resource production can be defined in several ways:
A task produces some amount of processing power for a resource at its start. The capacity produced is considered as non renewable which means that the produced capacity remains available even after the completion of the task. Note that a minimal amount of 0 is possible thus allowing modelisation of alternative resources. The type of resource production can be defined in several ways:
- By specifying a resource and a constant production parameter 'production'. In this case the resource production is constant other the execution of the task.
- By specifying a resource and a minimal 'minProd' and maximal 'maxProd' production parameters: In this case the resource production is a decision variable but is constant over the execution of the task.
- By specifying a cpresusage 'usage' (see resusage for further detail).
- By a set of alternative cpresusage 'optUsages': This makes it possible to model alternative resources. The type of resource production is defined by the resource usage passed in argument (see resusage for further detail).
- By a set of alternative cpresusage 'optUsages', a minimal 'minalt' and a maximal 'maxalt' number of alternative resources that may be produced: Between [minalt..maxalt] alternative productions from the set will be active which means that several resources will be chosen to be produced by the task. The type of resource production is defined by the resource usage passed in argument (see resusage for further detail)
Synopsis
procedure produces(task:cptask, production:integer, resource:cpresource)
procedure produces(task:cptask,minProd:integer, maxProd:integer, resource:cpresource)
procedure produces(task:cptask, usage:cpresusage)
procedure produces(task:cptask, optUsages:set of cpresusage)
procedure produces(task:cptask, optUsages:set of cpresusage, minalt:integer, maxalt:integer)
Arguments
|
task
|
the task
|
|
production
|
constant positive resource production
|
|
minProd
|
minimal resource production
|
|
maxProd
|
maximal resource production
|
|
resource
|
the resource to be produced
|
|
usage
|
the resource usage
|
|
optUsages
|
the set of alternatives resource production
|
|
minalt
|
minimal number of resources that must be produced
|
|
maxalt
|
maximal number of resources that may be produced
|
Example
The following example illustrates this:
model "Producer Consumer"
uses "kalis"
declarations
Masonry, Carpentry, Roofing, Windows, Facade, Garden, Plumbing,
Ceiling, Painting, MovingIn : cptask ! Declaration of tasks
money_available : cpresource ! Resource declaration
end-declarations
! 'money_available' is a cumulative resource with max. amount of 29$
set_resource_attributes(money_available,KALIS_DISCRETE_RESOURCE,29)
! Limit resource availability to 20$ in the time interval [0,14]
setcapacity(money_available, 0, 14, 20)
! Setting the task durations and predecessor sets
set_task_attributes(Masonry , 7 )
set_task_attributes(Carpentry, 3, {Masonry} )
set_task_attributes(Roofing , 1, {Carpentry} )
set_task_attributes(Windows , 1, {Roofing} )
set_task_attributes(Facade , 2, {Roofing} )
set_task_attributes(Garden , 1, {Roofing} )
set_task_attributes(Plumbing , 8, {Masonry} )
set_task_attributes(Ceiling , 3, {Masonry} )
set_task_attributes(Painting , 2, {Ceiling} )
set_task_attributes(MovingIn , 1, {Windows,Facade,Garden,Painting})
! Setting the resource consumptions
consumes(Masonry , 7, money_available )
consumes(Carpentry, 3, money_available )
consumes(Roofing , 1, money_available )
consumes(Windows , 1, money_available )
consumes(Facade , 2, money_available )
consumes(Garden , 1, money_available )
consumes(Plumbing , 8, money_available )
consumes(Ceiling , 3, money_available )
consumes(Painting , 2, money_available )
consumes(MovingIn , 1, money_available )
! Find the optimal schedule (minimizing the makespan)
if cp_minimize(getmakespan) then
cp_show_sol
else
writeln("No solution found")
end-if
end-model
Related topics

