MIQP

Topics covered in this section:

We now wish to express the fact that at most a given number MAXNUM of different assets may be selected into the portfolio, subject to all other constraints of the previous QP model. In Chapter 6 we have already seen how this can be done, namely by introducing an additional set of binary decision variables buy_s that are linked logically to the continuous variables:

Through this relation, a variable buy_s will be at 1 if a fraction frac_s greater than 0 is selected into the portfolio. If, however, buy_s equals 0, then frac_s must also be 0.

To limit the number of different shares in the portfolio, we then define the following constraint:

Implementation with Mosel

We may modify the previous QP model or simply add the following lines to the end of the QP model in the previous section: the problem is then solved once as a QP and once as a MIQP in a single model run.

 declarations
  buy: array(SHARES) of mpvar       ! 1 if asset is in portfolio, 0 otherwise
 end-declarations

! Limit the total number of assets
 sum(s in SHARES) buy(s) <= MAXNUM

 forall(s in SHARES) do
  buy(s) is_binary
  frac(s) <= buy(s)
 end-do

! Solve the problem
 minimize(Variance)

 writeln("With a target of ", TARGET," and at most ", MAXNUM,
         " assets, minimum variance is ", getobjval)
 forall(s in SHARES) writeln(s, ": ", getsol(frac(s))*100, "%")

When executing the MIQP model, we obtain the following solution output:

With a target of 9 and at most 4 assets,
 minimum variance is 1.248761905
1: 30%
2: 20%
3: 0%
4: 0%
5: 23.80952381%
6: 26.19047619%
7: 0%
8: 0%
9: 0%
10: 0%

With the additional constraint on the number of different assets the minimum variance is more than twice as large as in the QP problem.

Analyzing the solution

If we enable the Optimizer logging output display by setting XPRS_VERBOSE to 'true' we see the following information:

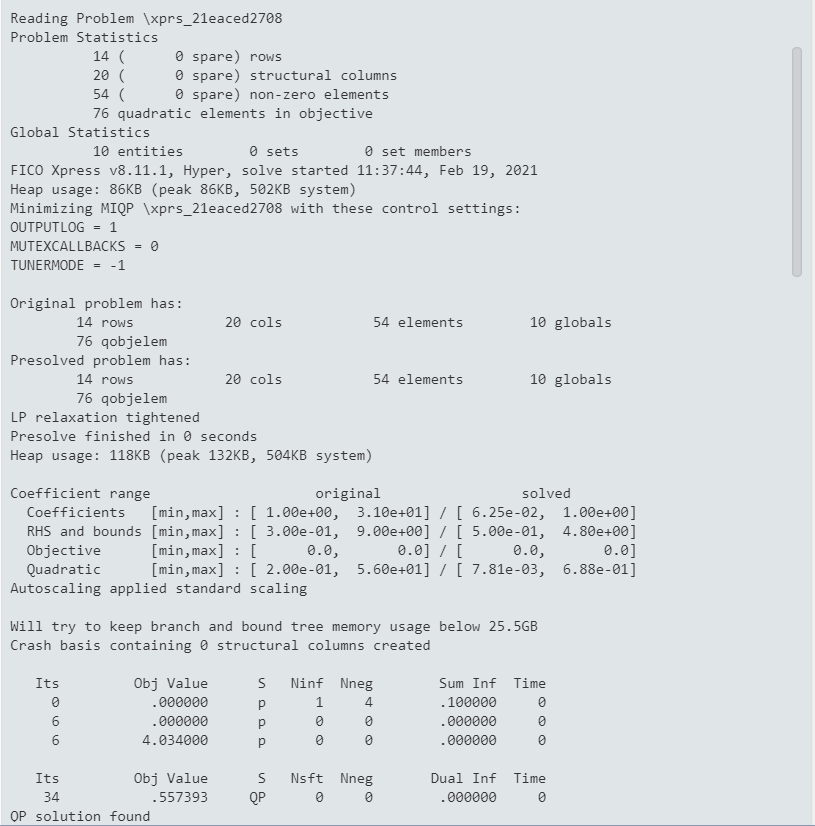
Figure 8.2: Detailed MIQP solution information

This is quite similar to the MIP statistics.

Just as with linear problems, the root solving as continuous problem is followed by a root cutting and heuristics phase (several integer feasible solutions are found by the heuristics):

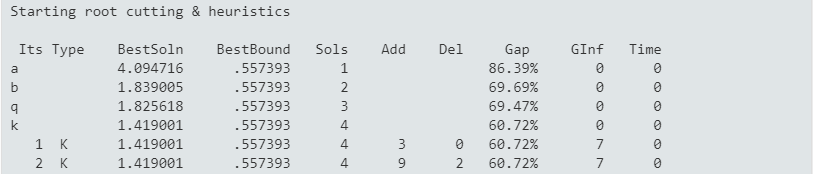
Figure 8.3: MIQP root cutting and heuristics

One more integer feasible solution is found during the Branch-and-Bound search. The search has been completed, this means that optimality of this solution has been proven (we may have chosen to stop the search, for example, after a given number of nodes, in which case it may not be possible to prove optimality or even to find the best solution).

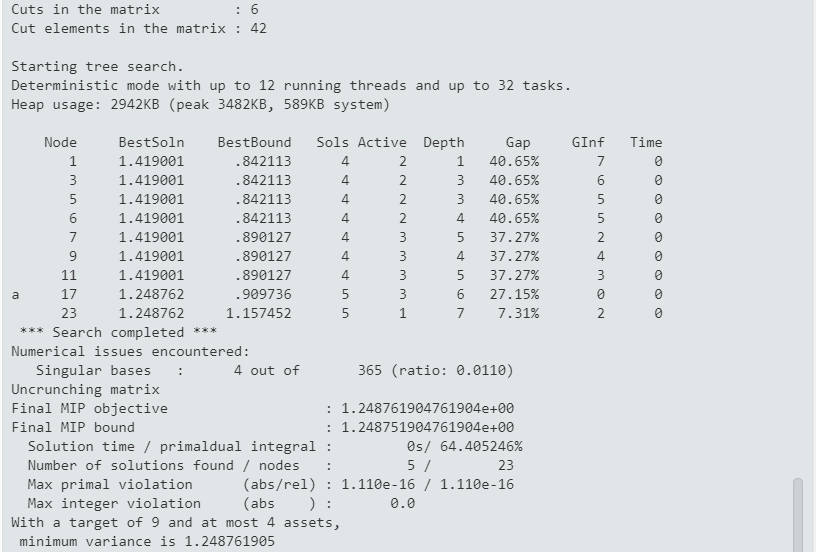
Figure 8.4: MIQP Branch-and-Bound search