Getting started with Mosel

Topics covered in this chapter:

Entering a model

In this chapter we will take you through a very small manufacturing example to illustrate the basic building blocks of Mosel.

Models are entered into a Mosel file using a standard text editor (do not use a word processor as an editor as this may not produce an ASCII file). If you have access to Windows, Xpress Workbench is the model development environment to use. The Mosel file is then loaded into Mosel, and compiled. Finally, the compiled file can be run. This chapter will show the stages in action.

The chess set problem: description

To illustrate the model development and solving process we shall take a very small example.

A joinery makes two different sizes of boxwood chess sets. The smaller size requires 3 hours of machining on a lathe and the larger only requires 2 hours, because it is less intricate. There are four lathes with skilled operators who each work a 40 hour week. The smaller chess set requires 1 kg of boxwood and the larger set requires 3 kg. However boxwood is scarce and only 200 kg per week can be obtained.

When sold, each of the large chess sets yields a profit of $20, and one of the small chess set has a profit of $5. The problem is to decide how many sets of each kind should be made each week to maximize profit.

A first formulation

Within limits, the joinery can vary the number of large and small chess sets produced: there are thus two decision variables (or simply variables) in our model, one decision variable per product. We shall give these variables abbreviated names:

small: the number of small chess sets to make large: the number of large chess sets to make

The number of large and small chess sets we should produce to achieve the maximum contribution to profit is determined by the optimization process. In other words, we look to the optimizer to tell us the best values of small, and large.

The values which small and large can take will always be constrained by some physical or technological limits: they may be constrained to be equal to, less than or greater than some constant. In our case we note that the joinery has a maximum of 160 hours of machine time available per week. Three hours are needed to produce each small chess set and two hours are needed to produce each large set. So the number of hours of machine time actually used each week is 3·small+ 2·large. One constraint is thus:

3·small + 2·large ≤ 160 (lathe-hours)

which restricts the allowable combinations of small and large chess sets to those that do not exceed the lathe-hours available.

In addition, only 200 kg of boxwood is available each week. Since small sets use 1 kg for every set made, against 3 kg needed to make a large set, a second constraint is:

1·small + 3·large ≤ 200 (kg of boxwood)

where the left hand side of the inequality is the amount of boxwood we are planning to use and the right hand side is the amount available.

The joinery cannot produce a negative number of chess sets, so two further non-negativity constraints are:

small ≥ 0
large ≥ 0

In a similar way, we can write down an expression for the total profit. Recall that for each of the large chess sets we make and sell we get a profit of $20, and one of the small chess set gives us a profit of $5. The total profit is the sum of the individual profits from making and selling the small small sets and the large large sets, i.e.

Profit = 5·small + 20·large

Profit is the objective function, a linear function which is to be optimized, that is, maximized. In this case it involves all of the decision variables but sometimes it involves just a subset of the decision variables. In maximization problems the objective function usually represents profit, turnover, output, sales, market share, employment levels or other `good things'. In minimization problems the objective function describes things like total costs, disruption to services due to breakdowns, or other less desirable process outcomes.

The collection of variables, constraints and objective function that we have defined are our model. It has the form of a Linear Programming problem: all constraints are linear equations or inequalities, the objective function also is a linear expression, and the variables may take any non-negative real value.

Solving the chess set problem

Building the model

The Chess Set problem can be solved easily using Mosel. The first stage is to get the model we have just developed into the syntax of the Mosel language. Remember that we use the notation that items in italics (for example, small) are the mathematical variables. The corresponding Mosel variables will be the same name in non-italic courier (for example, small).

We illustrate this simple example by using the command line version of Mosel. The model can be entered into a file named, perhaps, chess.mos as follows:

model "Chess"
 declarations
  small: mpvar                       ! Number of small chess sets to make
  large: mpvar                       ! Number of large chess sets to make
 end-declarations

 Profit:=  5*small + 20*large        ! Objective function
 Lathe:=   3*small + 2*large <= 160  ! Lathe-hours
 Boxwood:=   small + 3*large <= 200  ! kg of boxwood
end-model

Indentations are purely for clarity. The symbol ! signifies the start of a comment, which continues to the end of the line. Comments over multiple lines start with (! and terminate with !).

Notice that the character `*' is used to denote multiplication of the decision variables by the units of machine time and wood that one unit of each uses in the Lathe and Boxwood constraints.

The modeling language distinguishes between upper and lower case, so Small would be recognized as different from small.

Let's see what this all means.

A model is enclosed in a model / end-model block.

The decision variables are declared as such in the declarations / end-declarations block. Every decision variable must be declared. LP, MIP and QP variables are of type mpvar. Several decision variables can be declared on the same line, so

 declarations
  small, large: mpvar
 end-declarations

is exactly equivalent to what we first did. By default, Mosel assumes that all mpvar variables are constrained to be non-negative unless it is informed otherwise, so there is no need to specify non-negativity constraints on variables.

Here is an example of a constraint:

Lathe:=   3*small + 2*large <= 160

The name of the constraint is Lathe. The actual constraint then follows. If the `constraint' is unconstrained (for example, it might be an objective function), then there is no <=, >= or = part.

In Mosel you enter the entire model before starting to compile and run it. Any errors will be signaled when you try to compile the model, or later when you run it (see Chapter Correcting errors in Mosel models on correcting syntax errors).

Obtaining a solution using Mosel

So far, we have just specified a model to Mosel. Next we shall try to solve it. The first thing to do is to specify to Mosel that it is to use Xpress Optimizer to solve the problem. Then, assuming we can solve the problem, we want to print out the optimum values of the decision variables, small and large, and the value of the objective function. The model becomes

model "Chess (completed)"
 uses "mmxprs"                       ! We shall use Xpress Optimizer</p>

 declarations
  small,large: mpvar                 ! Decision variables: produced quantities
 end-declarations

 Profit:=  5*small + 20*large        ! Objective function
 Lathe:=   3*small + 2*large <= 160  ! Lathe-hours
 Boxwood:=   small + 3*large <= 200  ! kg of boxwood

 maximize(Profit)                    ! Solve the problem

 writeln("Make ", getsol(small), " small sets")
 writeln("Make ", getsol(large), " large sets")
 writeln("Best profit is ", getobjval)
end-model

The line

 uses "mmxprs"

tells Mosel that Xpress Optimizer will be used to solve the LP. The Mosel modules mmxprs module provides us with such things as maximization, handling bases etc.

The line

 maximize(Profit)

tells Mosel to maximize the objective function called Profit.

More complicated are the writeln statements, though it is actually quite easy to see what they do. If some text is in quotation marks, then it is written literally. getsol and getobjval are special Mosel functions that return respectively the optimal value of the argument, and the optimal objective function value. writeln writes a line terminator after writing all its arguments (to continue writing on the same line, use write instead). writeln can take many arguments. The statement

 writeln("small: ", getsol(small), " large: ", getsol(large) )

will result in the values being printed all on one line.

Running Mosel from a command line

When you have entered the complete model into a file (let us call it chess.mos), we can proceed to get the solution to our problem. We start Mosel at the command prompt by typing the following command

mosel execute chess.mos

and we will see output something like that below.

Make 0 small sets Make 66.6667 large sets Best profit is 1333.33

The Mosel command for executing the model can be abbreviated to

mosel exec chess

or simply

mosel chess

The model execution performed by the command execute comprises three stages:

1. Compiling chess.mos
2. Loading the compiled model
3. Running the model we have just loaded.

Instead of using execute, we can choose to explicitly generate the compiled model file chess.bim

mosel compile chess.mos

followed by

mosel run chess.bim

to load and run the compiled model.

Using Xpress Workbench

Under Microsoft Windows you may also use Xpress Workbench, a development studio type environment for working with your Mosel models. Xpress Workbench is a complete modeling and optimization development environment that presents Mosel in an easy-to-use Graphical User Interface (GUI), with a built-in text editor.

To execute the model file chess.mos you need to carry out the following steps.

• Start up Workbench.
• Open the model file by choosing File » Open. The model source is then displayed in the central window (the Workbench Editor).
• Click the Run button at the top of the window, making sure that the desired filename is selected in the input field to its left, or alternatively, choose Run » Run chess.mos.

The resulting screen display is shown in Figure Xpress Workbench screen after running chess.mos.

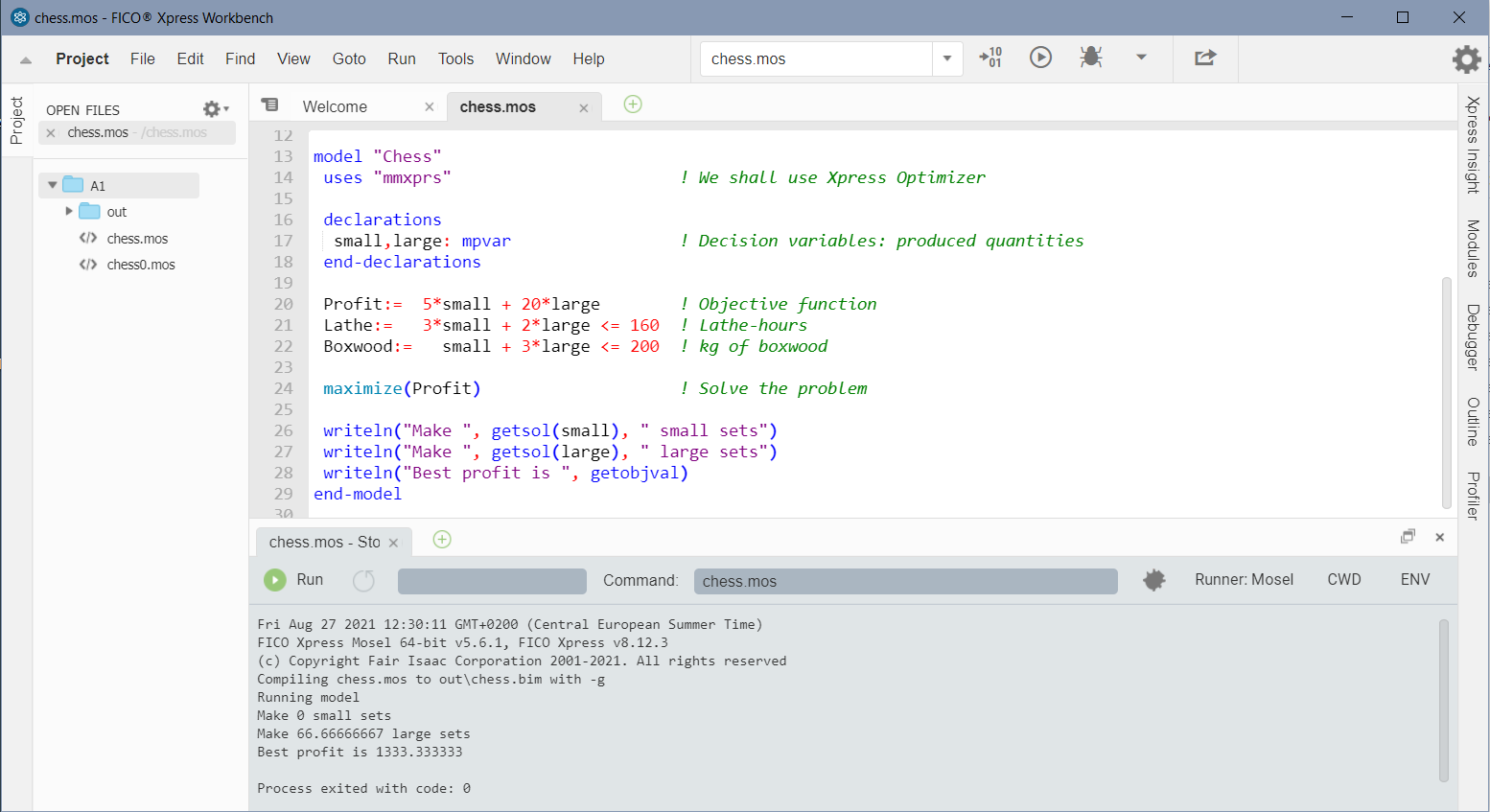
Figure 2.1: Xpress Workbench screen after running chess.mos

The logging pane at the bottom of the workspace is automatically displayed when compilation starts. If syntax errors are found in the model, they are displayed here, with details of the line and character position where the error was detected and a description of the problem, if available. If the model has been compiled successfully, this pane displays the output produced by running the model.

If the model is run in debug mode by selecting the Debug button Workbench makes all information about the solution available through the Debugger pane on the right border of the workspace window (see Figure Running chess.mos with Xpress Workbench in debug mode). By expanding the Variables entry in this pane, the solution and reduced cost values for decision variables are displayed. Dual and slack values for constraints may also be obtained.

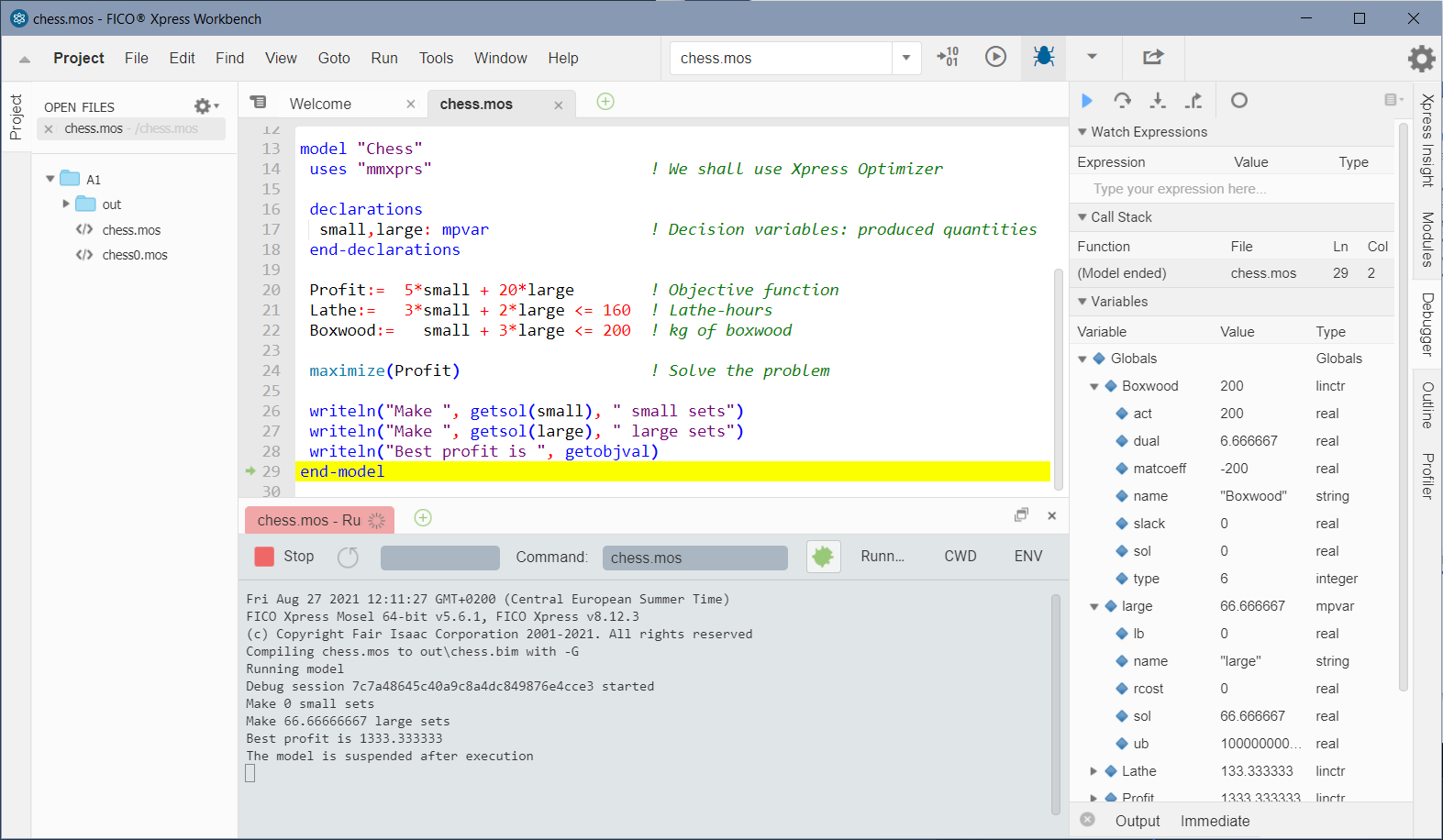
Figure 2.2: Running chess.mos with Xpress Workbench in debug mode