Robust shortest path
Topics covered in this section:
Problem description
Every day you are driving from your home to your work location. There are a number of alternative routes that you might use. You may think of these routes as a set of lines that connect nodes (=intersection points of routes). For every line (edge) we know the required travel time for getting from one end point to the other. What we don't know is the occurrence of roadworks or similar incidents that slow down traffic and hence cause delays.
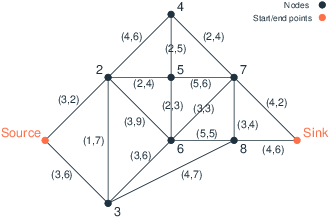
Figure 1: Road network
Figure Road network shows an example of a road network where the journey start and end points are marked as 'Source' and 'Sink' respectively. The label tuples (L,D) on the edges indicate the length (travel time) of an edge and the maximum delay D that may result from roadwork on this edge. In this data instance, the times in both directions for traveling along an edge are the same and the maximum delay in both senses is also the same, but in the general case the values might actually be different.
Mathematical formulation
Shortest path problem
The problem of finding the least cost route through a network is known as the shortest path problem. We can state this problem via binary variables usea associated with each arc a where usea=1 if arc a is selected and 0 otherwise.
For every node in the network except the source and sink nodes we establish a flow balance constraint: the sum of incoming travel is the same as the outgoing travel. The source node only has a single outgoing used arc, the sink node has a single incoming used arc. In the following, we define an arc a via its origin ARCa,1 and its destination node ARCa,2.
s.t. ∑a∈Arcs | ARCa,1=Source usea = 1, ∑a∈Arcs | ARCa,2=Sink usea = 1
∑a∈Arcs | ARCa,2=Source usea = 0, ∑a∈Arcs | ARCa,1=Sink usea = 0
∀ n ∈ Nodes - {Source,Sink}: ∑a∈Arcs | ARCa,2=n usea = ∑a∈Arcs | ARCa,1=n usea
∀ a∈Arcs: usea ∈{0,1}
In the model formulation above, we can add the delays caused by roadworks as an additional coefficient to the objective function so that they are taken into account by the shortest path calculation:
However, this means that we assume
- all delays take their maximum value and
- all roads incur delays.
These assumptions yield an overly conservative prediction. This case provides an upper bound on the total travel time estimate but it can certainly be considered as fairly unlikely to happen.
Robust optimization problem
The problem that we really wanted to state is
- delays take values up to their specified maximum value and
- up to N roads incur delays.
This means that the value of the delay per arc is not fixed, but uncertain. If delaya denotes the uncertain duration of the delay associates with arc a∈Arcs we can state the cardinality constrained uncertainty set as follows:
The resulting robust optimization problem then has the following form.
s.t. ∑a∈Arcs | ARCa,1=Source usea = 1, ∑a∈Arcs | ARCa,2=Sink usea = 1
∑a∈Arcs | ARCa,2=Source usea = 0, ∑a∈Arcs | ARCa,1=Sink usea = 0
∀ n ∈ Nodes - {Source,Sink}: ∑a∈Arcs | ARCa,2=n usea = ∑a∈Arcs | ARCa,1=n usea
∀ a∈Arcs: usea ∈{0,1}
delay ∈ U = {delay : | {delaya: delaya>0 }| ≤ N, 0≤delaya≤MAXDELAYa ∀ a∈Arcs}
Implementation
The following Mosel model roadworks.mos implements the robust optimization model from the previous section. Notice the use of cardinality on the uncertains delay to limit the total number of occurrences of roadworks to at most NWORK (the parameter for N) with a default value of 2. The uncertains that are used in such a cardinality constraint need to have explicit lower and upper bounds set. The solution reporting displays the selected arcs and the values of the uncertains for which a nonzero delay is chosen by the opponent.
model "road network"
uses "mmxprs", "mmrobust"
parameters
DATAFILE="roads_9.dat"
NWORK = 2 ! Number of roadworks
end-parameters
declarations
Nodes: range ! Set of nodes
ARC: array(Arcs:range,1..2) of integer ! Arc origins/destinations
LEN,MAXDELAY: array(Arcs) of real ! Length and max delay per arc
Source,Sink: integer ! Source and sink node numbers
use: array(Arcs) of mpvar ! 1 iff arc is used
TotalLength: robctr ! Objective function
delay: array(Arcs) of uncertain ! Uncertain delay
end-declarations
!**** Input datafile ****
initializations from DATAFILE
Nodes Arcs Source Sink ARC
[LEN,MAXDELAY] as "ArcData"
end-initializations
!**** Robust problem formulation ****
forall(a in Arcs) use(a) is_binary
! Sink and source of flow
sum(a in Arcs | ARC(a,1)=Source) use(a)=1
sum(a in Arcs | ARC(a,2)=Sink) use(a)=1
sum(a in Arcs | ARC(a,2)=Source) use(a)=0
sum(a in Arcs | ARC(a,1)=Sink) use(a)=0
! Flow balance in intermediate nodes
forall(n in Nodes-{Source,Sink})
sum(a in Arcs | ARC(a,2)=n) use(a) = sum(a in Arcs | ARC(a,1)=n) use(a)
! Random construction work on NWORK arcs
forall(a in Arcs) delay(a) <= MAXDELAY(a)
forall(a in Arcs) delay(a) >= 0
cardinality(union(a in Arcs) {delay(a)}, NWORK)
! Shortest path length
TotalLength:= sum(a in Arcs) (LEN(a)+delay(a))*use(a)
!**** Solving ****
minimize(TotalLength)
! Solution reporting
if getprobstat=XPRS_OPT then
writeln("Robust shortest path: ", getobjval)
writeln("Delay: ", sum(a in Arcs | use(a).sol>0) delay(a).sol)
forall(a in Arcs | use(a).sol>0)
writeln(if(ARC(a,1)=Source, "Source", string(ARC(a,1))), " -> ",
if(ARC(a,2)=Sink, "Sink", string(ARC(a,2))), "; ")
forall(a in Arcs | delay(a).sol>0)
writeln("Delay on (", ARC(a,1), ",", ARC(a,2), "): ", delay(a).sol)
else
writeln("No solution")
end-if
end-model Results
Figure Robust solution with 2 delays shows the path through the network defined by the robust solution; it has a total length of 21. The path it follows, i.e., Source → 2 → 5 → 6 → 7 → Sink, has a nominal length of 14, but if roads 2–5 and 5–6 have construction work we must add a total delay of 7. Given that these two roads have maximum delay (together with the combination of roads 2–5 and 6–7), any other combination of at most two roads with construction will result in a total duration of 21 minutes or less. The delay that we must add to the nominal length of the path is given by the sum of the solution values of the uncertains delay(a) associated with every arc a in the path. The solution values of the uncertains delay can be interpreted as providing an answer to the question 'which is the worst possible choice of delays for the selected path?'. The resulting values of the uncertains place the delay on the two arcs (2,5) and (5,6) for a total delay of 7.
Delay on (2,5): 4 Delay on (5,6): 3
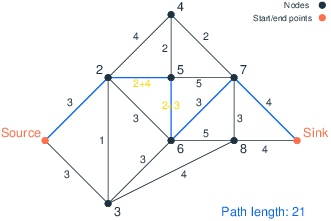
Figure 2: Robust solution with 2 delays
Consider now the solution in Figure Zero-delay solution, obtained by ignoring the delays caused by road work. The optimal path in this case is Source → 3 → 8 → Sink, with a total duration of 11. However, this is a very optimistic solution as in the worst case the roads Sink–3 and 3–8 may have construction work, in which case the travel time increases by 13 minutes to 24, clearly worse than the robust solution of 21 minutes.
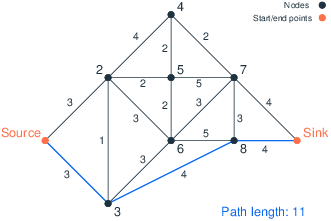
Figure 3: Zero-delay solution
Finally, let us take a look at the solution obtained by setting all arc costs to their maximum value, i.e., a shortest path computed on a graph where all edges are assumed to have their maximum delay. As shown in Figure Maximum-delay solution, the solution is the path Source → 2 → 4 → 7 → Sink, and has a duration of 27 minutes. Under the assumption that at most two roads have construction work, this travel time is meaningless: in fact, the nominal travel time is 13 minutes and the worst-case travel time is obtained with road work on 2–4 and 4–7, which add 10 minutes to the solution and hence yield a total travel time of 23, still worse than the robust shortest path of 21 depicted above.
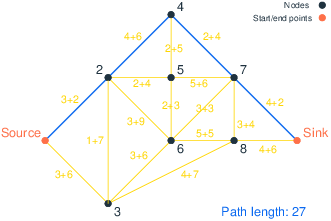
Figure 4: Maximum-delay solution
We recap the above results in Table Path costs, which shows the worst-case travel times for the paths determined by the three approaches (robust for N=2, shortest path with nominal values, shortest path where all roads have maximum delay) in five cases: no road work, road work in N=1, 2, or 3 edges of the graph, and road work everywhere, i.e. N is infinite.
| N | 0 | 1 | 2 | 3 | +inf | Path |
|---|---|---|---|---|---|---|
| Robust | 14 | 18 | 21 | 24 | 28 | Source → 2 → 5 → 6 → 7 → Sink |
| Nominal | 11 | 18 | 24 | 30 | 30 | Source →3 →8 → Sink |
| All delays | 13 | 19 | 23 | 25 | 27 | Source → 2 → 4 → 7 → Sink |
The values in this table can be obtained by fixing the arc selection in the robust problem to a given path and re-solving it for different values of N (i.e. we determine the worst-case delay for a given path that satisfies all constraints of the robust problem).
Note that, under the assumption we have made at the beginning of this section, the only solution that truly solves the problem with minimum worst-case travel time is the one that was found using the uncertains to model our knowledge, albeit limited, of the road works in this network.
© 2001-2024 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

