Robust unit commitment
Topics covered in this section:
Problem description
The unit commitment problem consists in scheduling the power generation level of a set of generators to meet the power demand. In order for a power system to operate safely, the power generation must equal the demand at any time (the so-called power balance constraints) Failing to satisfy this requirement may result in serious issues, possibly causing a black out.
The power generation level of a power generating unit depends on its commitment. When the unit is switched off, no power is produced, only when it has been started the unit can generate electricity. Due to technical constraints, the power generation level must lie within a band describing safe operation. For the vast majority of unit types, the minimum power generation level is an important parameter when deciding whether to start a particular unit or not.
Another parameter that plays an important role in the decision whether to start a unit is its startup cost. Units with low startup cost could be started and shut down multiple times during a planning period, while units with high cost will preferrably be kept running once started.
For the sake of simplicity, other considerations like ramp rate constraints, shutdown costs or the various reserve types are omitted from the present model.
Example: We shall consider the case of day-head unit commitment scheduling. This operational planning task consists in determining on a day for the next, the startup and shutdown phases of the generating units in order to be able to safely satisfy the next day's power demand. However, the exact demand is not known for sure at the time of scheduling, and hence it is considered an uncertain parameter of the optimization problem. Common practice for dealing with this uncertainty is to commit a larger number of units than strictly required to be sure to have sufficient upward and downward power generation reserve. In the following we will show how to apply robust optimization techniques to take into account this uncertainty more efficiently.
We are going to present two robust implementations of the unit commitment problem resulting in plans for which the unit commitment decisions do not have to be changed in real time. More precisely, the suggested unit commitment schedules make sure that enough power generation capacity is available to supply the actual demand without requiring any last minute unit startups or shutdowns. The first model is based on a scenario uncertainty set, it ensures that the unit commitment status will not require any modification even if the real power demand is different from the forecast. In this problem it is assumed that the power demand realization will be similar to either the forecast or some historical power demand curve. The second model, based on a cardinality uncertainty set, guarantees that the unit commitment status will not require any modification even if up to 'k' generating units are simultaneously forced in outage.
Robust against power demand variation
Typical unit commitment robustness against power demand variation is achieved by adding constraints to bound the difference between the total power generation and the total available power generation capacity of running units. This value is known as the upward power generation level and defines the maximum power demand increase that can be safely supplied without requiring new unit startup. This empirical value is arbitrarly determined from historical power demand.
We will see how the robust optimization framework can be used to seamlessly implement similar constraints by replacing the reserve requirement by a set of robust constraints formed from historical power demand. These historical data and the power demand forecast are used to determine the real power demand. This real power demand is modeled with the scenario uncertainty sets. The figure Historical power demand and forecast presents the next day's historical power demand of the last 6 years alongside with the forecasted power demand.
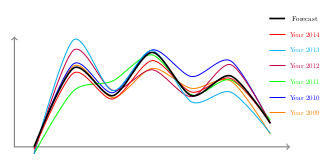
Figure 6: Historical power demand and forecast
Robust against the N-k contingency
Typical unit commitment robustness against unit forced outage is achieved by analysing the impact of a contingency resulting in loss of k generating units. If the total lost generation is greater than the upward reserve from the remaining generating units, then the system is at risk and demand cannot be fully sustained. Running such a simulation is an important task and provides insights about the security of the power system. Unfortunately, if it can prove the inability of the schedule to survive k, the model will fail to suggest how to improve the schedule to satisfy the safety constraint.
A robust optimization formulation can be used to simulate the loss of k running units and to suggest the startup and shutdown of new units to safely supply the power demand. The cardinality uncertainty sets will be used to model the outage state of a unit.
Mathematical formulation
The set Horizon of consecutive time periods describes the planning horizon of the study. Time periods t∈Horizon have different lengths LENt. Each time period t∈Horizon is associated with a power demand DEMt.
The set Units denotes the set of available power generation units. The minimum power generation level of a unit is PMINu, and its maximum capacity is PMAXu. The startup cost of a single unit is CSTRu, and the cost of running it at the minimum power generation level is CMINu. The marginal power production cost above PMINu for each hour is CADDu.
Each unit u is associated with three decision variables. The binary variable startut equals 1 if the unit u is starting at the beginning of time period t. The binary variable workut equals 1 if the unit u is up and running during the whole time period t. At last, the variable paddut is set to the power generation level of the unit u during time period t.
Original Unit Commitment Problem
The objective function, to be minimized, is the expected operation cost. The operation cost is composed of the startup cost and the generation cost. It can be expressed as follows:
| ∑ |
| u∈Units,t∈Horizon |
The startup constraints describe the time period(s) during which the unit is starting. They can expressed as follows:
startu1 ≥ worku1 - workuT, ∀u∈Units, if t=0
The maximum power generation level constraints limit the power generation level of a unit. These constraints are stated as:
The power balance constraints ensure that the total power production equals the power demand at any time. They are formulated by these equations:
| ∑ |
| u∈Units |
Load Robust Unit Commitment Problem
The Load Robust Unit Commitment problem extends the Original Unit Commitment problem by constraining the unit commitment to be safe under power demand variation. Historical power demands for the last years are known.
The scenario uncertainty set
Let Udem be the set of possible future power demands. Let Years be the set of past years that should be taken into account, and HDEMyt the demand for the time period t of the year y. Then the uncertainty set can be expressed as follows:
Robust constraints
| ∑ |
| u∈Units |
The reformulation engine will efficiently handle the resulting, potentially large number of constraints, even with large sets of historical data.
The N-k Contingency-Constrained Unit Commitment Problem
The N-k Contingency-Constrained Unit Commitment problem extends the Original Unit Commitment problem as to make sure that the committed power generation units can supply the load, even if k generators are simultaneously forced in outage. The uncertain eut represents the forced outage event, and the uncertainty set is the set of units that are in forced outage.
The power generation units cannot efficiently be turned on or off at short notice. At the time of scheduling the units, the demand is not known for sure and we must make sure that the total maximum power output capacity of the committed units is greater than the highest demand forecast. Similarly, the total minimum power generation level must be lower than the lowest demand forecast.
The cardinality uncertainty set
Let Uoutage be the set describing groups of combinations of k units in forced outage. This uncertainty set can be expressed as follows:
| ∑ |
| u∈Units |
Robust constraints
| ∑ |
| u∈Units |
| ∑ |
| u∈Units |
These two robust constraints contain the same uncertains. Because uncertains are used to model worst case situation for a particular constraint, the same uncertain may have different values in each constraint.
Implementation
The Original Unit Commitment Implementation
The Mosel code printed below implements and solves the original formulation of the unit commitment problem.
declarations NT = 7 ! Number of time periods TIME = 1..NT ! Time periods PLANTS = 1..4 ! Power generation plant UNITS: set of string ! Power generation units LEN, DEM: array(TIME) of integer ! Length and demand of time periods PMIN,PMAX: array(PLANTS) of integer ! Min. and max output of a generator type CSTART: array(PLANTS) of integer ! Start-up cost of a generator CMIN: array(PLANTS) of integer ! Hourly cost of gen. at min. output CADD: array(PLANTS) of real ! Cost/hour/MW of prod. above min. level PLANT: array(UNITS) of integer ! Unit generation plant YEARS: range ! Historical years HDEM: array(YEARS,TIME) of integer ! Historical demand profiles start: array(UNITS,TIME) of mpvar ! Is generation unit starting ? work: array(UNITS,TIME) of mpvar ! Is generation unit up ? padd: array(UNITS,TIME) of mpvar ! Production above min. output level end-declarations initializations from 'a6electr_ro_simple.dat' LEN DEM PMIN PMAX CSTART CMIN CADD PLANT HDEM end-initializations
! Create decision variables
forall(u in UNITS, t in TIME) do
start(u,t) is_binary
work(u,t) is_binary
end-do
! Objective function: total daily cost
Cost:= sum(u in UNITS, t in TIME) (CSTART(PLANT(u))*start(u,t) +
LEN(t)*(CMIN(PLANT(u))*work(u,t) + CADD(PLANT(u))*padd(u,t)))
! Number of generators started per period and per type
forall(u in UNITS, t in TIME)
start(u,t) >= work(u,t) - if(t>1, work(u,t-1), work(u,NT))
! Limit on power production range
forall(u in UNITS, t in TIME)
padd(u,t) <= (PMAX(PLANT(u))-PMIN(PLANT(u)))*work(u,t)
! Power balance
forall(t in TIME)
sum(u in UNITS) (PMIN(PLANT(u))*work(u,t) + padd(u,t)) = DEM(t)
! Symmetry breaker
forall(t in TIME, p in PLANTS)
forall(u1, u2 in UNITS | PLANT(u1) = PLANT(u2) and u1<u2)
work(u1,t) >= work(u2,t)
!**** Solving and solution reporting ****
! Solve the original problem
minimize(Cost)
writeln("\n=== Nominal case ===\n")
print_solution
! Add robust constraints
robust_demand
! Solve robust the problem
setparam("ROBUST_UNCERTAIN_OVERLAP", true)
minimize(Cost)
writeln("\n=== Robust against demand variation ===\n")
print_solution
The following output printing routines are invoked from the model shown above:
!**** Print highest loss of load in case of worst case scenario realization
procedure print_risk
write("\n", strfmt("Loss of load",20))
forall(t in TIME) do
s:= sum(u in UNITS) (work(u,t).sol*PMAX(PLANT(u))) ! Total capacity
v:= maxlist(DEM(t), max(y in YEARS) HDEM(y,t)) ! Hist. peak demand
if(s < v) then
write(strfmt(v-s,8))
else
write(strfmt("",8))
end-if
end-do
end-procedure
!**** Solution printing ****
procedure print_solution
writeln("Total cost: ", getobjval)
write(strfmt("Time period ",-20))
ct:=0
forall(t in TIME) do
write(strfmt(ct,5), "-", strfmt(ct+LEN(t),2), "")
ct+=LEN(t)
end-do
write("\n",strfmt("Up Units",-20))
forall(t in TIME) write(strfmt(sum(u in UNITS) work(u,t).sol,8))
write("\n", strfmt("Gen. Pwr.",20))
forall(t in TIME)
write(strfmt(sum(u in UNITS) (work(u,t).sol*PMIN(PLANT(u))+padd(u,t).sol),8))
write("\n", strfmt("Gen. Cap.",20))
forall(t in TIME)
write(strfmt(sum(u in UNITS) (work(u,t).sol*PMAX(PLANT(u))),8))
write("\n", strfmt("Res. Dn",20))
forall(t in TIME) write(strfmt(sum(u in UNITS) (padd(u,t).sol),8))
write("\n", strfmt("Res. Up",20))
forall(t in TIME)
write(strfmt(sum(u in UNITS) work(u,t).sol*PMAX(PLANT(u)) - DEM(t),8))
print_risk
writeln
end-procedure
The Load Robust Unit Commitment Implementation
The extension to scenario-based robust optimization is implemented by the following subroutines.
!**** Helper routine to create scenario uncertain set ****
public procedure makescenario(a:array(r1:range,c1:range) of integer,
u:array(c2:range) of uncertain)
declarations
aa:dynamic array(r0:range,U:set of uncertain) of real
end-declarations
forall(i in r1, j in c1|exists(a(i,j)) and exists(u(j)),n as counter) do
aa(n,u(j)):=a(i,j)
end-do
scenario(aa)
end-procedure
!**** Robust against past scenario ****
public procedure robust_demand
declarations
demand: array(TIME) of uncertain ! Uncertain power demand
end-declarations
! Add uncertainty set (time correlation)
makescenario(HDEM,demand)
! Security reserve upward
forall(t in TIME) sum(u in UNITS) PMAX(PLANT(u))*work(u,t) >= demand(t)
end-procedure
The N-k Contingency-Constrained Unit Commitment Implementation
Replacing the call to the procedure robust_demand by a call to the procedure robust_contingency printed below will turn the problem formulation into a N-k contingency-constrained unit commitment model.
The example also demonstrates how to use the value of the uncertain to extract meaningful information about the units which are the most critical ones for the system.
writeln("\n")
!***************************Subroutines***************************
!**** Ensure enough power production capacity allows to
!**** satisfy load even if 'k' units are forced in outage.
procedure robust_contingency(k: integer)
forall(t in TIME, u in UNITS) create(outage(u,t))
forall(t in TIME, u in UNITS) outage(u,t) >= 0
! If the unit is forced in outage, the total capacity
! of the generating units are lost
forall(t in TIME, u in UNITS) outage(u,t) <= 1
! forall(t in TIME) sum(u in UNITS) outage(u,t) <= k
forall(t in TIME) cardinality(union(u in UNITS | exists(outage(u,t))) {outage(u,t)}, k)
forall(t in TIME)
RobCtrMaxDem(t) :=
sum(u in UNITS) PMAX(PLANT(u))*work(u,t) -
sum(u in UNITS) PMAX(PLANT(u))*work(u,t)*outage(u,t) >= DEM(t)
! In order to reduce the number of variables we reuse
! outage() and let the solver do the variable duplication
! by setting the ROBUST_UNCERTAIN_OVERLAP parameter
setparam("ROBUST_UNCERTAIN_OVERLAP",true)
forall(t in TIME)
RobCtrMinDem(t) :=
sum(u in UNITS) PMIN(PLANT(u))*work(u,t) -
Results
Let us now take a look at the results generated by the three models. The Original Unit Commitment Problem is used as the baseline scenario and the results of the two robust versions are compared against it.
For all three model formulations, a feasible unit commitment which satisfies the technical constraints and supplies the load is found.
The characteristics of the power generation units used in the test instances (number of units per type, minimum and maximum generation levels, fixed cost when running at minimum level, variable cost between minimum and maximum generation levels, start-up cost) are summarized in Table Description of power generators.
| Unit type | Number | Pmin | Pmax | Fix cost | Add. MW cost | Start-up cost |
|---|---|---|---|---|---|---|
| 1 | 10 | 750 | 1750 | 2250 | 2.7 | 5000 |
| 2 | 4 | 1000 | 1500 | 1800 | 2.2 | 1600 |
| 3 | 8 | 1200 | 2000 | 3750 | 1.8 | 2400 |
| 4 | 3 | 1800 | 3500 | 4800 | 3.8 | 1200 |
Table Nominal case presents results of the nominal optimization problem. For each time period, the number of started units is presented (Up Units), along with the generation power (Gen. Pwr.). The generation capacity (Gen. Cap.) is the total maximum power generation available from the started units. The columns 'reserve down' (Res. Dn.) and 'reserve up' (Res. Up) respectively show the maximum load decrease or load increase that can be safely supported without requiring startup or shutdown of any units.
For example, during the first period (0-6) the load can increase from 12000 kWh (power demand forecast) to 13250 kWh (power demand forecast + reserve up) without having to start up new units.
The last two lines present the maximum loss-of-load in case the worst scenario realizes. For the demand variation, the worst scenario is the realization of the load profile that requires the highest power generation increase. For the contingency planning, the worst scenario occurs when the k 'critical' units are forced in outage. The criticality of a unit depends on its power generation level and total reserve. A unit without reserve up is critical, as is a unit supplying a very large share of the total load.
| 0-6 | 6-9 | 9-12 | 12-14 | 14-18 | 18-22 | 22-24 | |
|---|---|---|---|---|---|---|---|
| Up units | 8 | 18 | 15 | 20 | 15 | 17 | 11 |
| Gen. Pwr. | 12000 | 32000 | 25000 | 36000 | 25000 | 30000 | 18000 |
| Gen. Cap. | 13250 | 37750 | 27250 | 44750 | 27250 | 34250 | 19250 |
| Res. Dn | 3850 | 10050 | 8450 | 10450 | 8450 | 9850 | 6250 |
| Res. Up | 1250 | 5750 | 2250 | 8750 | 2250 | 4250 | 1250 |
| Loss of load | |||||||
| Demand variation | 0 | 1395 | 1491 | 0 | 2592 | 0 | 0 |
| 2 Contingencies | 2750 | 1250 | 1750 | 0 | 1750 | 2750 | 2750 |
| 0-6 | 6-9 | 9-12 | 12-14 | 14-18 | 18-22 | 22-24 | |
|---|---|---|---|---|---|---|---|
| Up Units | 8 | 18 | 15 | 20 | 15 | 17 | 11 |
| Gen. Pwr. | 12000 | 32000 | 25000 | 36000 | 25000 | 30000 | 18000 |
| Gen. Cap. | 13250 | 39250 | 28750 | 44750 | 30250 | 37250 | 19250 |
| Res. Dn | 3850 | 9450 | 7850 | 10450 | 7250 | 8650 | 6250 |
| Res. Up | 1250 | 7250 | 3750 | 8750 | 5250 | 7250 | 1250 |
| Loss of load | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
If the nominal case is applied, then in case of demand variation, there is a risk of not supplying 1395 kWh of demand during the morning peak. Common sense would be to start up a new unit in order to cover the risk for all time periods when there is a risk of loss of load. However, the results from the robust formulation for the demand variation problem presented in Table Robust against demand variation show that it is possible to overcome the risk merely by changing the type of committed units.
| 0-6 | 6-9 | 9-12 | 12-14 | 14-18 | 18-22 | 22-24 | |
|---|---|---|---|---|---|---|---|
| Up Units | 9 | 18 | 16 | 20 | 15 | 17 | 11 |
| Gen. Pwr. | 12000 | 32000 | 25000 | 36000 | 25000 | 30000 | 18000 |
| Gen. Cap. | 19750 | 39250 | 32250 | 44750 | 33250 | 38750 | 25250 |
| Res. Dn | 850 | 9450 | 6050 | 10450 | 6050 | 8050 | 3850 |
| Res. Up | 7750 | 7250 | 7250 | 8750 | 8250 | 8750 | 7250 |
| Loss of load | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The loss of load for the 2 contingencies case highlights that there is a risk of not being able to supply 2750 kWh during the initial periods. It means that about 20% of the total demand will not be covered. Indeed there is only 1250 kWh of upward reserve available, which means that even if just a single unit running at full capacity is lost (1500 kWh) then the power demand cannot be supplied. Like in the previous case, the common sense conclusion would be to start up new units. However, the results from the robust formulation for the 2 contingencies problem presented in Table Robust against 2 contingencies show that it is possible to find a unit commitment schedule without risking load disconnection and without committing too many new units (and hence incurring higher startup costs).
References
The presented nominal unit commitment model is based on a problem described in the book 'Applications of optimization with Xpress-MP' [GHP02].
© 2001-2024 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

