Solution Methods

Topics covered in this chapter:

This chapter provides a summary of the methods used within FICO Xpress Global to solve MINLP problems. While the solution method is based on the branch-and-bound paradigm, and most of its features are those described in the general manual, solving an MINLP problem requires an extra set of tools to provide a guaranteed optimal solution or, if the time limit is reached, a valid bound. Specifically, FICO Xpress Global implements the following specialized tools for solving MINLPs:

• reformulation of an MINLP;
• creation of an LP relaxation of an MINLP;
• branching on continuous variables, or spatial branching;
• bound reduction;
• heuristics.

This chapter describes these tools in detail.

Reformulation of an MINLP

We consider an optimization problem where a possibly nonlinear, non-convex function must be minimized either unconstrained or subject to a set of constraints, also possibly nonlinear and non-convex. We additionally consider constraints on the variables in the form of lower and upper bounds and integrality. The notation below will help us navigate all methods described in this chapter.

\( \begin{array}{llll} \min & f_0({\mathbf{x}})\\ \textrm{s.t.} & f_i({\mathbf{x}}) \le 0 & \forall i=1,2,\ldots{},m\\ & x_j \in [\ell_j,u_j] & \forall j=1,2,\ldots{},n\\ & x_j \in \mathbb Z & \forall j\in J \end{array} \)

Here the set of all variables is represented by the vector \( \mathbf{x} \). Both the objective function and the constraints are functions of \( \mathbf{x} \). All variables have lower and upper bounds, and a subset \( J \) of them is also integral.

Similar to mixed-integer linear programming problems, how a problem is formulated can strongly impact how efficiently it is solved.

Factorable functions

We begin with an assumption on how the problem is formulated: all functions \( f_i \), for \( i = 0, 1, \ldots{}, m \), are factorable: this means that they result from the composition of a finite set of operators on variables and constants. In other words, the closed form of these functions is known; user functions computed by calling, e.g., a C/Java/Python function are currently not supported. The allowed set of operators is the same we use to write nonlinear expressions, including but not restricted to the standard operators \( \{+, -, \times, /, x^y\} \), univariate functions like \( \{\sqrt{\cdot}, \sin, \log\} \) and many more. For an exhaustive list of the almost twenty supported nonlinear functions, see the section Internal Functions in the FICO Xpress Nonlinear manual. Examples of factorable functions, composed from those operators, include:

\( \begin{array}{lll} \sum_{j=1}^n e^{x_j}x_j^3 & x_1 \sin(x_2) & x\sin\left(\frac{1}{x}\right)\\ x_1^3 - 3x_1^2 + 3 x_1 - 1 \qquad & \sqrt{\sum_{j=1}^n x_j^2}\qquad & \prod_{j=1}^n\log(x_j)\\ \end{array} \)

Functions that are not factorable are for example \( x_1\sin(x_2)\textrm{myfun}(x_3) \), where myfun is implemented as a black-box function using, for instance, our interface for user functions; Because myfun is not defined in closed form from the above set of operators, FICO Xpress Global will not be able to find a globally optimal solution, and instead, local optimization solvers in the FICO Xpress suite, such as SLP or Knitro, should be used.

From here on, we assume all constraints and the objective function are specified as factorable functions. We will use a small example to explain all steps taken by the Optimizer:

\( \begin{array}{llll} \min & x_1^2 - 2 x_2^4\\ \textrm{s.t.} & x_1 x_2 \ge 4\\ & x_1 + \frac{1}{2} e^{x_2^2} \le 4 \\ & 0 \le x_1 \le 4\\ & -1 \le x_2 \le 3 \\ & x_2 \in \mathbb Z\\ \end{array} \)

Reformulation and auxiliary variables

When solving an MINLP with the FICO Xpress Global solver, from the solver log one can notice that several new variables and constraints are introduced. Below we explain the process that leads to this possible increase in problem size.

Every factorable MINLP is solved by creating a set of new variables assigned to subexpressions appearing in the problem. These new variables are called auxiliary variables, or auxiliaries for short. Each forms a pair with a portion of an expression appearing in all functions of the problem, namely a subexpression that uses only one operator of the set mentioned above. For the example MINLP, we add five auxiliaries, which we call \( w_1, w_2, w_3, w_4, w_5 \) and which are assigned as follows:

\( \begin{array}{lll} w_1 = x_1^2;\qquad & w_3 = x_1 x_2;\qquad & w_5 = e^{w_4}\\ w_2 = x_2^4; & w_4 = x_2^2&\\ \end{array} \)

Introducing auxiliaries does not change the problem substantially, but it helps solve it. Now we can rewrite the problem as

\( \begin{array}{llll} \min & w_1 - 2 w_2\\ \textrm{s.t.} & w_3 \ge 4\\ & x_1 + \frac{1}{2} w_5 \le 4 \\ & w_1 = x_1^2\\ & w_2 = x_2^4\\ & w_3 = x_1 x_2\\ & w_4 = x_2^2\\ & w_5 = e^{w_4}\\ & 0 \le x_1 \le 4\\ & -1 \le x_2 \le 3 \\ & 0 \le w_1 \le 16\\ & 1 \le w_2 \le 81\\ & -4 \le w_3 \le 12\\ & 0 \le w_4 \le 9\\ & 1 \le w_5 \le e^9\\ & w_2, x_2 \in \mathbb Z\\ \end{array} \)

The following three observations shall help to understand why the reformulation is performed this way. First, note that the only nonlinear part of the problem is now in the constraints that define the auxiliaries – the objective function and the original constraints have become linear by replacement with some auxiliaries. Second, these auxiliaries also have lower and upper bounds because the expression associated with each of them is bounded. Finally, because \( x_2 \) is integer, so is \( w_2 \).

Creation of an LP relaxation of an MINLP

The second step in solving an MINLP is creating a relaxation of the nonlinear constraints that consists only of linear constraints. A valid relaxation provides a lower bound on the optimal objective value and can be exploited in a branch-and-bound algorithm that is similar to what the FICO Xpress Optimizer uses for mixed-integer linear programming problems.

To this purpose, all constraints that determine the relationship between an auxiliary and a nonlinear function are relaxed by one or more linear constraints. The term relaxation here refers to the idea that all feasible solutions to the original problem are also feasible for the problem with the amended linear inequalities.

For example, the constraint \( w_1 = x_1^2 \), which is nonlinear and non-convex, can be relaxed by four linear constraints as shown below (note that any \( (x_1,w_1) \) in the bound intervals specified above and satisfying \( w_1 = x_1^2 \) also satisfy all of these linear constraints), the first three of which are so-called McCormick inequalities, while the fourth one is an Outer Approximation cut:

\( \begin{array}{l} w_1 \le 4 x_1\\ w_1 \ge 0\\ w_1 \ge 8x_1 - 16 \\ w_1 \ge 4x_1 - 4 \\ \end{array} \)

Similar sets of linear constraints can be created to replace the other nonlinear constraints \( w_2 = x_2^4 \), \( w_3 = x_1 x_2 \), \( w_4 = x_2^2 \) and \( w_5 = e^{w_4} \). We call such linear inequalities convexification cuts because they allow us to create a convex (LP) relaxation of a non-convex nonlinear problem. The result is a problem with only linear constraints and a linear objective function, and solving it yields a valid lower bound to the original MINLP.

Such a problem is handled by FICO Xpress Global's branch-and-cut solver, which applies the same machinery as the classic MILP solver and extended features that are suited to MINLPs.

Refining the relaxation

The MILP solver in the FICO Xpress Optimizer is a branch-and-cut algorithm: a branch-and-bound solver that also adds linear inequalities at, possibly, every branch-and-bound subproblem to speed up computation and obtain a tight lower bound (in case of a minimization problem) of the optimal objective function value.

These linear inequalities are added after the first (root) relaxation in an iterative fashion, and also during tree search.

Such linear inequalities added in the MILP framework exploit the structure and features of the MILP problem. Common names for these classes of inequalities are Gomory cuts, Mixed-Integer Rounding cuts, etc.

FICO Xpress Global uses a similar framework to amend the initial LP relaxation with extra linear inequalities for each auxiliary variable multiple times in the root-cutting phase and also during the branch-and-bound. This helps refine the relaxation shown above in much the same way as an MILP solver.

Running branch-and-bound on an MINLP

The above section has pointed out the role of convexification cuts in solving an MINLP. Another key factor in an efficient MINLP solver is branching, which subdivides a single branch-and-bound subproblem into two or more subproblems by employing extra constraints on each subproblem.

For solving an MINLP, it is necessary to generalize the MILP paradigm: in the latter, an integer (or binary) variable \( x_i \) that takes a fractional value \( x^*_i \) in a subproblem can be branched upon, thus creating two new subproblems: the first has the additional constraint \( x_i \le \lfloor x^*_i \rfloor \), while \( x_i \ge \lceil x^*_i \rceil \) is added to the second.

Because of the nonlinear, non-convex constraints that appear in MINLPs, it can be necessary to branch on continuous variables as well as on integer variables.

Spatial Branching

Consider again the auxiliary \( w_1 \) and its associated expression \( w_1 = x_1^2 \), which is nonlinear and non-convex. Variable \( x_1 \) is continuous and bounded between 0 and 4. Figure 4.1 shows the graph of this function and, in the shaded area, the feasible region created by the following four convexification cuts:

\( \begin{array}{lll} \textcolor{red}{w_1 \le 4 x_1} & \qquad & w_1 \ge 0 \\ \textcolor{blue}{w_1 \ge 8x_1 - 16} & & \textcolor{green}{w_1 \ge 4 x_1 - 4}. \\ \end{array} \)

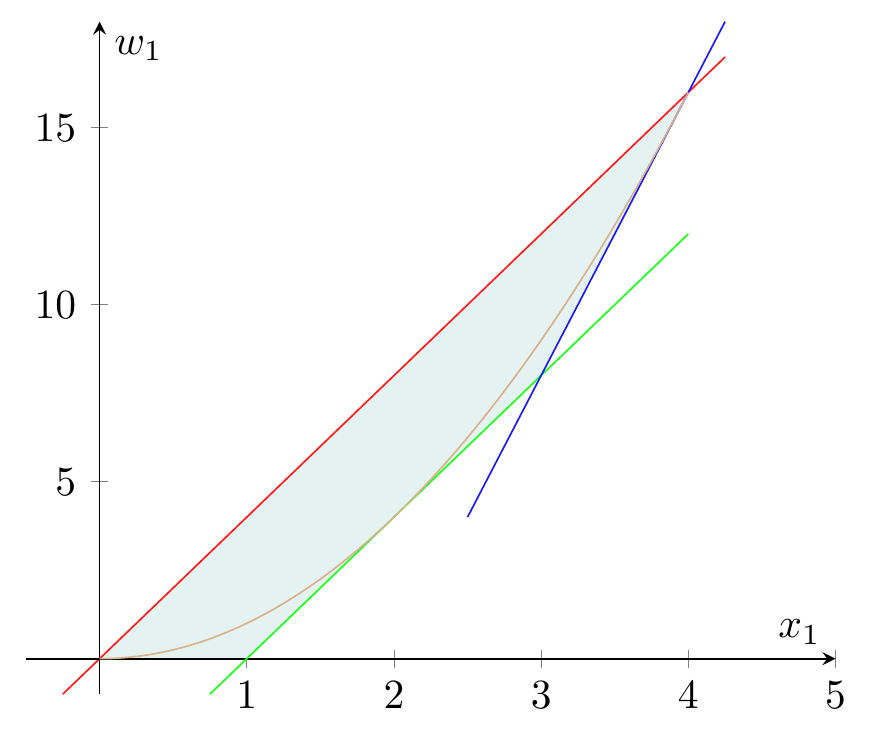
Figure 4.1: A linear relaxation of the square function

As mentioned above, these linear inequalities are satisfied by all points \( (x_1,w_1) \) which satisfy \( w_1 = x_1^2 \). While more convexification cuts can be added to strengthen the relaxation, one can easily see that no such cut exists for the point \( (x_1,w_1) = (2,5) \). The only way to eliminate this solution is a branch operation, even though \( x_1 \) is a continuous variable.

Branching on continuous variables is called spatial branching for historical reasons, but the effect is similar to that of branching on integer variables: two new subproblems are created, and the tree search continues.

The FICO Xpress Global solver extends the branch-and-bound algorithm that works for the FICO Xpress Optimizer to continuous variables in MINLP problems. While the structure of the two algorithms is essentially the same, the FICO Xpress Global solver tackles MINLP problems by equipping the MILP solver with extra features for reducing the process of solving an MINLP to that of solving an MILP.

Bound reduction

Convexification cuts, mentioned above, are one of the crucial MINLP solving capabilities of the FICO Xpress Global solver. The quality of such cuts, measured by how tight the resulting lower bound is, depends strongly on the lower and upper bounds of all problem variables, including the auxiliaries.

For this reason, one of the main presolving components used by the Global solver is bound reduction, sometimes also referred to as propagation or node presolving. Bound reduction is a class of algorithms that, given the lower and upper bounds of all variables, can obtain tighter bounds on one or more variables that any feasible and optimal solution has to satisfy. Bound reduction techniques might exclude some feasible solutions but ensure that always at least one optimal solution remains, thereby not changing to optimal objective value for the reduced problem.

Given an MINLP in the general form \( \min\{f(\mathbf{x}): \mathbf{x}\in X\} \), the purpose of a bound reduction algorithm is to tighten the bounds on all variables \( x_i \) of the problem. One common technique is a straight generalization of what is used in MILP.

Feasibility-based bound reduction

Perhaps the best-known form of bound reduction uses the original constraints of the MINLP to infer better bounds on both original and auxiliary variables.

Consider the part of our MINLP example that stems from the second constraint, \( x_1 + \frac{1}{2} w_5 \le 4 \) and consider the variables involved in it, i.e., \( x_1 \), \( x_2 \), and \( w_4 \), \( w_5 \), with initial bound intervals equal to \( [0,4] \), \( [-1,3] \), \( [1, e^9] \), and \( [0, 9] \) respectively. We copy that portion here for convenience:

\( \begin{array}{l} x_1 + \frac{1}{2} w_5 \le 4 \\ w_5 = e^{w_4}\\ w_4 = x_2^2\\ 0 \le x_1 \le 4\\ -1 \le x_2 \le 3 \\ 0 \le w_4 \le 9\\ 1 \le w_5 \le e^9\\ x_2 \in \mathbb Z\\ \end{array} \)

The constraint \( x_1 + \frac{1}{2} w_5 \le 4 \) implies, given that \( x_1 \ge 0 \), that \( w_5 \le 8 \lt e^3 \), which in turn leads to new upper bounds on \( w_4 \) and \( x_2 \), i.e., \( w_4 \le \ln(8) \) and \( x_2 \le \sqrt{\ln(8)} \). Integrality of \( x_2 \) further tightens its upper bound to \( \lfloor\sqrt{\ln(8)}\rfloor=1 \).

Bound reductions like the ones above usually have a knock-on effect on other elements of the problem. Tighter bounds on some variables often lead to tighter bounds of other variables and so on. Moreover, tighter variable bounds frequently lead to tighter LP relaxations, see the beginning of this chapter, and therefore to a better bound on the optimal solution value and potentially even better feasible solutions being found more quickly.

The above bound reduction technique is often denoted as feasibility-based bound reduction and uses the nonlinear information from the problem. Other techniques are known that further restrict the variable bounds, but some of them are computationally expensive, and their use is normally limited to a small number of calls.

Heuristics

The FICO Xpress Global solver uses heuristics to find a feasible solution to an MINLP. Similar to an MILP solver, heuristics can be called both at the beginning of the solution process or during branch-and-bound.

To find feasible solutions, enforcing nonlinear constraints while working with an LP relaxation is not easy. For this reason, heuristics use a nonlinear optimization solver such as SLP or Knitro. Both are nonlinear solvers that can find a locally optimal solution, hence of objective value possibly inferior to that of the global optima. The effectiveness of such an approach stems from the efficiency of the local solvers, which can find a local solution in a fraction of the time it would require an MINLP solver to find a global optimum.

One technique to find feasible solutions is to fix all the integer variables to an integral value and then solve the resulting continuous nonlinear problem. If the resulting solution is feasible for the restricted problem, it is also feasible for the original problem and can be used as a cutoff. This procedure is regularly applied to integer solutions of the LP relaxation (which are typically not feasible for the nonlinear constraints), as well as solutions found by the MILP heuristics.