Basic Usage

Topics covered in this chapter:

Using FICO Xpress Global inside the Console Optimizer

You can use FICO Xpress Global directly within the Console Optimizer, an interactive command line interface to the Optimizer. The Console Optimizer is started from the command line using the following syntax:

C:\> optimizer

Note that the example shows the command as if it were input from the Windows Command Prompt (i.e., it is prefixed with the command prompt string C:\>). Windows users can also start the Console Optimizer by typing optimizer into the "Run ..." dialog box in the Start menu.

The Console Optimizer provides a quick and convenient interface for operating on a single problem loaded into the Optimizer. Currently, the Console Optimizer supports reading nonlinear problems from NL files, files in extended MPS format and LP format (for quadratic problems). From the Console Optimizer, you can easily (i) set controls for handling and solving the problem and (ii) query attributes of the problem and its solution information.

Useful features of the Console Optimizer include a help system, auto-completion of command names, and integration of system commands.

Typing "help" will list the various options for getting help. Typing "help commands" will list available commands. Typing "help attributes" and "help controls" will list the available attributes and controls, respectively. Typing "help" followed by a command name or control/attribute name will list the help for this item.

Nonlinear instances should be read by the READPROB command and solved to global optimality by the OPTIMIZE or the NLPOPTIMIZE command.

Let's consider an example that reads a nonlinear problem in NL format, solves it, prints the optimal objective value on screen, and writes the solution vector to a file.

[xpress C:\] readprob myMinlp.nl
[xpress C:\] optimize
[xpress C:\] NLPOBJVAL
42
[xpress C:\] writeslxsol myNonlinearSol.slx
[xpress C:\] quit

Note that you can either pass different flags to the (nlp)optimize command or use the NLPSOLVER control to switch between solving a problem to global or local optimality, provided both Xpress Global and Xpress Nonlinear are licensed. Per default, Xpress Global will be called. In the following example, the first call to nlpoptimize will solve to local optimality, the second to global optimality, the third one will be the same as the first one.

[xpress C:\] readprob myMinlp.nl
[xpress C:\] nlpoptimize -s
[xpress C:\] NLPOBJVAL
50
[xpress C:\] readprob myMinlp.nl
[xpress C:\] nlpoptimize
[xpress C:\] NLPOBJVAL
42
[xpress C:\] NLPSOLVER=1
[xpress C:\] readprob myMinlp.nl
[xpress C:\] nlpoptimize
[xpress C:\] NLPOBJVAL
[xpress C:\] quit

For more details on using the Console Optimizer, we refer to the corresponding section in the FICO Xpress Optimizer documentation.

Using FICO Xpress Global from the callable library

In the previous section, we looked at the Console Optimizer interface and introduced some essential functions that all FICO Xpress Optimizer users should be familiar with. In this section, we expand on the discussion and include some essential functions of the library interface.

Init and Free

Before you can use FICO Xpress Global from any of the interfaces, the Optimizer library must be initialized, and the licensing status successfully verified.

When the Console Optimizer is started from the command line, the initialization and licensing security checks happen immediately, and the results are displayed with the banner in the console window. For the library interface users, the initialization and licensing are triggered by a call to the library function XPRSinit, which must be made before any of the other Optimizer library routines can be successfully called. If the licensing security checks fail to check out a license, then library users can obtain a string message explaining the issue using the function XPRSgetlicerrmsg.

Once the Optimizer functionality is no longer required, the user should release the license and any system resources the Optimizer holds. The Console Optimizer releases these automatically when the user exits the Console Optimizer with the QUIT or STOP command. For library users the Optimizer can be triggered to release its resources with a call to the routine XPRSfree, which will free the license checked out in the earlier call to XPRSinit.

if (XPRSinit(NULL)) {
  char message[512];
  XPRSgetlicerrmsg(message, sizeof(message));
  printf("Problem with XPRSinit, licensing error: %s\n", message);
  exit(-1);
}

[...] /* Code goes here */

XPRSfree();

In general, library users will call XPRSinit once when their application starts and then call XPRSfree before it exits.

The Problem Pointer

The Optimizer provides a container or problem pointer to contain an optimization problem and its associated controls, attributes, and any other resources the user may attach to help construct and solve the problem. The Console Optimizer has one of these problem pointers to provide the user with loading and solving functionality. This problem pointer is automatically initialized when the Console Optimizer is started and released when it stops.

Unlike the Console Optimizer, library interface users can have multiple problem pointers coexisting simultaneously in a process. The library user creates and destroys a problem pointer using the routines XPRScreateprob and XPRSdestroyprob, respectively. In the C library interface, the user passes the problem pointer as the first argument in routines that are used to operate on the problem pointer's data. Note that it is recommended that the library user destroy all problem pointers before calling XPRSfree.

XPRSprob prob;
XPRScreateprob(&prob);
XPRSreadprob(prob, "myMINLP.nl", "");
XPRSoptimize(prob,"",NULL,NULL);
XPRSdestroyprob(prob);

Controls can be set and queried, and attributes can get queried with the typical FICO Xpress Optimizer functions. The following example again reads a problem but now accesses some attributes on the problem size and the optimal solution value. Additionally, it uses the output arguments of XPRSoptimize to print information about the solution process and the found solution.

XPRSprob prob;
int solvestatus, solstatus;
int ncol, nrow;

/* create an environment and read a problem */
XPRSinit(NULL);
XPRScreateprob(&prob);
XPRSreadprob(prob, "myMINLP.nl", "");

/* get and print matrix dimensions */
XPRSgetintattrib(prob, XPRS_INPUTCOLS, &ncol);
XPRSgetintattrib(prob, XPRS_INPUTROWS, &nrows);

/* solve and print results */
XPRSoptimize(prob,"",&solvestatus,&solstatus);
if (solvestatus == XPRS_SOLVESTATUS_COMPLETED)
  printf("Optimization finished successfully\n");
else
  printf("Optimization terminated with status %d", solvestatus);
if (solstatus >= XPRS_SOLSTATUS_OPTIMAL || solstatus == XPRS_SOLSTATUS_FEASIBLE) {
  double objval;
  XPRSgetdblattrib(prob, XPRS_NLPOBJVAL, &objval);
  printf("We found a solution with objective value %f\n", objval);
}

/* Goodbye! */
XPRSdestroyprob(prob);
XPRSfree();

Optimizing and querying a problem

The following example contains a code snippet that will query the solution values of an (MI)NLP that has been solved with FICO Xpress Global. Note that you should use XPRSgetsolution to get a nonlinear solution, — not XPRSgetlpsol or XPRSgetmipsol. In addition, one should not use the ..mip.. methods, but always use the corresponding ..nlp.. methods (or those without qualifiers), even for MINLP problems.

int cols;
int solstatus;
double *x;
...
XPRSoptimize(prob,"");
XPRSgetintattrib(prob,XPRS_INPUTCOLS,&cols);
x = malloc(cols*sizeof(double));
XPRSgetsolution(prob, &solstatus, x, 0, cols-1);
if (solstatus == XPRS_SOLSTATUS_OPTIMAL || solstatus == XPRS_SOLSTATUS_FEASIBLE) {
    printf("We found a solution\n");
}

Loading a non-convex quadratic optimization problem

Another example shows how non-convex quadratic problems can be loaded via the API functions XPRSloadqp, XPRSloadqcqp, XPRSloadmiqp, or XPRSloadmiqcqp. The latter is the most comprehensive. The others are "derivatives" with fewer input arguments since specific structures like discrete variables or quadratic constraints are not present in the respective problem classes. We use XPRSloadmiqp to create an optimization problem with non-convex objective \( x^2-3xy-y^2 - 6x \) (presented as \( 0.5 x^T Q x + c^T x \), where \( Q = (2, -3; -3, -2) \) of which the upper triangular submatrix is given), subject to a linear constraint \( x + y \leq 1.9 \) and the requirement that \( x \) must be integer.

/* Row data */
int nrows        = 1;            /* Number of constraints */
char rowtype[]   = {'L'};        /* Row types */
double rhs[]     = {1.9};        /* Right-hand side values */
double *range    = NULL;         /* Range values - none in this example */

/* Column data */
ncols            = 2;            /* Number of variables */
double objcoef[] = {-6, 0};      /* Linear objective function coefficients */
double lbound[]  = {0, 0};       /* Lower bounds on the columns */
double ubound[]  = {XPRS_PLUSINFINITY, XPRS_PLUSINFINITY}; /* Upper bounds (all +infinity) */

/* Data for the linear part of the constraints */
int start[]      = {0, 1, 2};	 /* Start positions of the columns in matcoef.
                                    There are nVar+1 entries, the last
                                    indicating where the next column would
                                    start if there was one. Here x1 and x2
                                    both appear once linearly. */
int *collen      = NULL;         /* Number of elements in each column - not
                                    needed thanks to the last (optional) entry
                                    in nColStart */
int rowind[]     = {0, 0};       /* Row indices for the matrix elements */
double rowcoef[] = {1, 1};       /* Matrix elements - arranged by column */

/* Quadratic data */
nquad = 3;                       /* Number of elements in the upper triangular of Q */
int objqcol1[] = {0, 0, 1};      /* Index of first variable in quadratic term Q */
int objqcol2[] = {0, 1, 1};      /* Index of second variable in quadratic term Q */
double dquad[] = {2, -3, -2};    /* Values of upper triangular entries of Q, notice factor of 2 for diagonal */

/* Integrality data */
int nentities = 1;               /* Number of MIP entities (i.e. discrete variables) */
int entind[] = {0};              /* Indices of MIP entities (i.e. discrete variables) */
char coltype[]={'I'};            /* Integrality type, in this case integer */
nsets = 0;                       /* No special ordered sets */

...

XPRSloadmiqp(prob, "myprob", ncols, nrows, rowtype, rhs,
                range, objcoef, start, collen, rowind,
                rowcoef, lbound, ubound, nquad, objqcol1, objqcol2,
                dquad, nentities, nsets, coltype, entind, NULL,
                NULL, NULL, NULL, NULL);

Loading a nonlinear optimization problem

Our final example shows the creation of an MINLP problem with both quadratic and nonlinear expressions by creating variables and using them in string-defined expressions. The problem is

\( \begin{array}{ll} \min & 2 x_1 + \frac{1}{2} 7 x_2^2 \\ \textrm{s.t.} & x_1^4 + x_2^4 - 100 x_3 \le 3\\ & x_1 + 2 x_2 + 5 x_3 \ge 1\\ & \sqrt{x_1 - x_2} + \log{x_3} \ge 3\\ & x_1 \in \mathbb Z\\ & x_1, x_2, x_3 \ge 0\\ & x_2 \le 200 \end{array} \)

and it contains linear, quadratic, and nonlinear elements. While the linear and quadratic elements can be introduced in a single call, one needs to use other functions to add nonlinear expressions to the problem.

XPRSprob prob = NULL;

/* Initialise problem object */
XPRScreateprob(&prob);

/* Row data */
int nRow       = 3;                  /* Number of constraints */
char rowType[] = {'L','G','G'};      /* Row types */
double rhs[]   = {3,1,3};            /* Right-hand side values */
double *range  = NULL;               /* Range values - none in this example */
char rowName[] = "con1\0con2\0con3"; /* Constraint names */

/* Column data */
int nVar     = 3;                   /* Number of variables */
double obj[] = {2,0,0};             /* Linear objective function coefficients */
double lb[]  = {0,0,0};             /* Lower bounds on the columns */
double ub[]  = {XPRS_PLUSINFINITY,
                200,
                XPRS_PLUSINFINITY}; /* Upper bounds */
char varName[] = "x1\0x2\0x3";      /* Variable names */

/* Data for the linear part of the constraints */
int nColStart[]  = {0,1,2,4};    /* Start positions of the columns in matcoef.
                                    There are nVar+1 entries, the last
                                    indicating where the next column would
                                    start if there was one. Here x1 and x2
                                    appear once linearly, x3 appears twice. */
int *nColElem    = NULL;         /* Number of elements in each column - not
                                    needed thanks to the last (optional) entry
                                    in nColStart */
int rowInd[]     = {1,1,0,1};    /* Row indices for the matrix elements */
double matcoef[] = {1,2,-100,5}; /* Matrix elements - arranged by column */

This first part declares only the linear part of the problem. For the quadratic elements (only one appears in the objective function, i.e., \( \frac{1}{2}7x_2^2 \)) and the integer variable \( x_1 \) more data is necessary before the call to XPRSloadmiqp, after which we also assign names to variables and constraints:

int nquad = 1;
int objqcol1[] = {1}; /* First index (i.e. x2) in the quadratic term in the objective*/
int objqcol2[] = {1}; /* Second index (x2 here as well) */
double quadcoef[] = {7}; /* Coefficient of quadratic term */

int nentities = 1, nsets = 0;  /* This problem has one MIP entity
                                  (i.e. discrete variable)
                                  and no special ordered sets */

int entind[] = {0};  /* The only discrete variable is x1 */

char coltype[]={'I'};

XPRSloadmiqp(prob, "myMINLP", nVar, nRow, rowType, rhs, range,
             obj, nColStart, nColElem, rowInd, matcoef,
             lb, ub,
             nquad, objqcol1, objqcol2, quadcoef,
             nentities, nsets, coltype, entind, NULL, NULL, NULL, NULL, NULL);

/* Add constraints and variable names */
XPRSaddnames(prob, 1, rowName, 0, 2);
XPRSaddnames(prob, 2, varName, 0, 2);

Adding nonlinear terms is possible by entering strings with variable names, constants, and operators separated by spaces. The expression \( x_1^4 + x_2^4 \) can be represented by the string x1 \( \widehat{} \) 4 + x2 \( \widehat{} \) 4, where x1 and x2 are the names assigned to \( x_1 \) and \( x_2 \), respectively, through the second call to XPRSaddnames. We can set the nonlinear terms for a constraint with the function XPRSnlpchgformulastr, as in the snippet below. The call to XPRSoptimize with option "x" allows for solving the problem to global optimality.

XPRSnlpchgformulastr(prob, 0, "x1 ^ 4 + x2 ^ 4");
XPRSnlpchgformulastr(prob, 2, "sqrt ( x1 - x2 ) + log ( x3 )");

XPRSoptimize(prob, "", NULL, NULL);

XPRSdestroyprob(prob);

Modelling via Mosel or Python

For an example of how to model a nonlinear problem via FICO Xpress Mosel, we refer to the FICO Xpress Nonlinear Manual.

For Python, the script below shows how to solve the classical Kissing Number Problem, a sphere packing problem in \( d \) dimensions where one seeks to determine if \( p \) unit spheres (i.e. spheres of radius 1) can be placed around a unit sphere at the center in such a way that each surrounding sphere touches the central one.

We solve this problem by creating variables for the coordinates of the centers of all surrounding spheres and an extra variable \( z \), which we minimize, which represents the degree of superposition of spheres to one another. The model, which is quadratic yet non-convex, is as follows:

\( \begin{array}{lll} \min & z\\ \textrm{s.t.} & \sum_{k=1}^d (x_{ik} - x_{jk})^2 \ge 4 - z & \forall i=1,2,\ldots{},p, \forall j=1,2,\ldots{},p, i \lt j\\ & \sum_{k=1}^d x_{ij}^2 = 4 & \forall i=1,2,\ldots{},p\\ \end{array} \)

Its Python implementation is below. Note that this version is parametric in the number \( d \) of dimensions and the number \( p \) of spheres. The value of \( z \) in an optimal solution to the above is zero if and only if it is possible to arrange \( p \) spheres, otherwise no such arrangement exists.

import xpress as xp

d = 2  # number of dimensions
n = 6  # hypothetical number of unit spheres around a unit sphere centered at (0,0)
N = range(n)

p = xp.problem()

x = p.addVariables(n, d, lb=-2, ub=2)  # coordinates of the centers (can't be
                                       # below -2 or above 2)

z = p.addVariable()  # violation of superposition of spheres

p.setObjective(z)  # z is to be minimized

# orbital spheres don't overlap each other unless z > 0
p.addConstraint(xp.Sum((x[i,:] - x[j,:])**2) >= 4 - z for i in N for j in N if i<j)

# orbital spheres have distance two to the central one at the origin so that they don't overlap it
p.addConstraint(xp.Sum(x[i,:]**2) == 4 for i in N)

p.optimize('x')

Visualizing the solution for two dimensions and any value of \( p \) is easy through the matplotlib module with the snippet below, which results, for \( p=6 \), in Figure Solution of the KNP in two dimensions for p=6 below.

import matplotlib.pyplot as plt

center = plt.Circle((0,0), 1, color='red')

# Create circles whose center is the solution obtained from the above
# problem
spheres = [plt.Circle(xp.evaluate([x[i,j] for j in range(d)],
                                  problem=p), 1, color='blue') for i in N]

fig, ax = plt.subplots()

ax.set_xlim((-3,3))
ax.set_ylim((-3,3))

ax.add_patch(center)
for i in N:
    ax.add_patch(spheres[i])

plt.show()

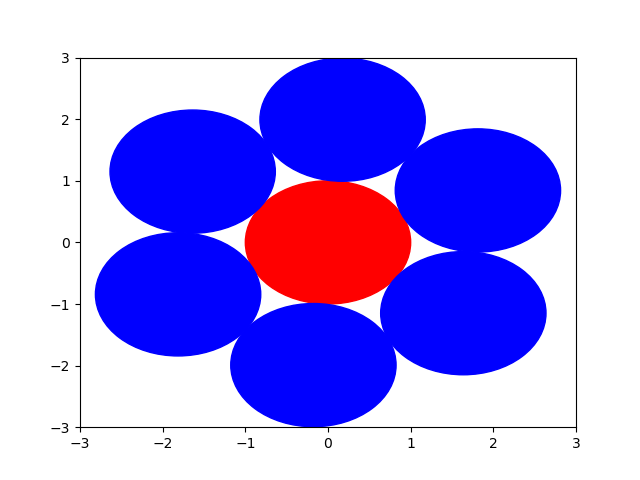
Figure 2.1: Solution of the KNP in two dimensions for p=6

Dealing with unboundedness and infeasibility

A linear optimization problem, with or without binary or integer variables, that does not admit any feasible solution is called infeasible, and the FICO Xpress Optimizer has efficient algorithms to determine and investigate the infeasibility of an LP problem.

Similarly, a (mixed-integer) linear optimization problem that does not admit a finite optimum is called unbounded. Both for LP and MILP problems, determining unboundedness can be done efficiently and often leads to re-writing the optimization model.

In MINLP, infeasibility can be diagnosed similarly to MILP: either the LP relaxation of the original MINLP problem is infeasible or, through a branch-and-bound run, it is determined that no feasible solution exists for the MINLP.

However, unboundedness requires special care in MINLP. Unlike for an MILP problem, where unboundedness of its LP relaxation implies unboundedness of the MILP, for MINLP problems an unbounded relaxation warrants further investigation.

As an example, the problem \( \min\{x: x^3 - x^2 \ge 0\} \), which is reformulated to \( \min\{x: w_1 - w_2 \ge 0, w_1 = x^3, w_2 = x^2\} \), does not have lower or upper bounds on either auxiliary variable due to the absence of strong bounds on \( x \). Although it is clear that the optimal solution is \( x=0 \), the first LP relaxation is unbounded. In general, even though bound reduction can help tighten the bounds on all variables and thus make the problem bounded, there are edge cases where this does not happen.

FICO Xpress Global handles this case as follows: first, if the initial root relaxation is found to be unbounded, new lower and upper bounds are imposed on every original (i.e., non-artificial) variable: \( -B \le x_i \le B \), where \( B \) is determined by the control GLOBALBOUNDINGBOX and can be set by the user (and the same control can be used to disable this procedure altogether). Second, the LP relaxation is solved again. If the new (restricted) LP relaxation is still unbounded, the same bounds are imposed on the auxiliary variables as well, thus making the problem surely bounded.

Regardless of the value of GLOBALBOUNDINGBOX, if the above procedure is carried out on an MINLP, i.e., if the initial LP relaxation is found to be unbounded, this implies that the solution produced by FICO Xpress Global is not a guaranteed globally optimal solution, since the artificial bounds may exclude an optimal solution. If an optimal solution for the new problem is found, the solution status will be LOCALLY_OPTIMAL rather than OPTIMAL.

This remarks again how important it is to formulate an optimization problem in the correct way. In order to make unboundedness unlikely and hence retain the chance of finding an optimal solution, it is useful to impose valid bounds on as many variables as possible.

File Formats for MINLP problems

Three file formats can be used to read an MINLP problem into FICO Xpress Global: NL, MPS, and LP, whose file extensions are .nl, .mps, and .lp, respectively. Whether it is with the READPROB command on the Optimizer Console or through the XPRSreadprob and XPRSwriteprob functions in the C library, these three file formats can be used for loading or saving an MINLP problem from/to a file.

The NL format is universally used to input MINLP with nonlinear, non-quadratic objective functions and constraints. As for the MPS and LP formats, their extension to handle nonlinear, non-quadratic expressions is not standard and should only be used to read and write MINLP problems for use by FICO Xpress Optimizer.

The MPS and LP formats are instead universally accepted for MINLPs with quadratic (both convex and non-convex) objective and constraints, and the same holds for NL files.