Introduction

Topics covered in this chapter:

Contents of this manual

This reference manual documents version 13.4.0 of Xpress Kalis.

(c) Copyright 2000-2024 Artelys S.A. and Fair Isaac Corporation. All rights reserved.

This document and the software described in this document are furnished under a license or non-disclosure agreement, and may be used or copied only within the terms of such a license or non-disclosure agreement.

Constraint programming overview

Constraint programming (CP) is a software technology becoming more widespread thanks to many successes whith effective solving of large, real-life, particularly combinatorial, problems. It provides a powerful technique for different problems such as scheduling, timetabling, resource allocation, or network configuration.

Research results from different fields (operations research, artificial intelligence, discrete mathematics, graph theory) are all involved in the core of Constraint Programming packages. Constraint Programming allows for representing many problems in a way which is very close to a natural language description, thanks to semantic constraints. Benefits are important: fast prototyping, compact code, easy modification, and good performance. It allows for specifying powerful decision support systems.

In order to have a quick overview of this technique, here are the basic elements required for a problem description:

A constraint satisfaction problem (CSP) is defined by:

• A set of decision variables V = {x₁,...,x_n}
• For each variable, a set (or a range) of possible values called its domain
• A set of constraints on these variables.

The arity of a constraint corresponds to the number of variables that it involves. For discrete variables, domain values do not have to be consecutive (for example {1, 4, 6, 8}). For continuous variables, the domain is modelled as an interval.

An interesting notion is the constraint graph:

A CSP can be represented by a non-oriented graph where the edges symbolize the links between constraints and variables. The Figure Constraint graph corresponding to the CSP shows an example of a constraint graph for the following CSP:

Variables: x, y, z
Constraints: x ≠ y, y ≠ z, z ≠ x

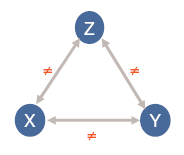
Figure 1.1: Constraint graph corresponding to the CSP

A solution to a CSP is an assignment of a value (belonging to its domain) to every variable, satisfying all the constraints.

In CP, constraints are used actively to deduce infeasible values and delete them from the domains of variables. This mechanism is called constraint propagation. It represents the core of Constraint Programming systems. Each constraint computes impossible values for its variables and informs other constraints. This process continues as long as new deductions are made.

Constraint propagation is associated with tree search techniques in order to find solutions or prove optimality. Each node and each decision will induce constraint propagation automatically. Many specific and efficient algorithms will be used in this propagation, but do not need to be known by the end-user. This allows persons who are familiar with problem modeling to quickly use such techniques for optimization or generation of solutions.

Solutions of a discrete CSP can be found by a systematic search on the set of possible assignments of values to variables. Other interval techniques are applied for continuous variables.

One may wish to find:

• just one feasible solution, without any choice preference
• all the solutions
• an optimal solution (or at least a nearly optimal solution) that optimizes a certain objective function defined on a subset of the variables of the problem

Solution search methods can be classified in two categories:

• Search methods that explore the space of the partial assignments
• Search methods that explore the space of complete assignments, generally in a stochastic way

The main reason for representing a problem as a CSP is that the formulation of the problem as a CSP is close to the original one in that: variables of the CSP directly correspond to the problem entities and the constraints can be expressed in a natural way without any translation to a set of linear inequalities as in the Mathematical Programming framework. This formulation is thus clearer, solutions are easier to represent, and search heuristics more direct.

What is Xpress Kalis for Mosel?

The Xpress Kalis Module for Mosel provides access to the FICO^® Xpress Kalis Constraint Programming solver by Artelys from the Mosel language. The software is provided in the form of a Mosel module, kalis. Xpress Mosel must be installed in order to be able to use the kalis module. The graphical environment Xpress Workbench can be used to work with Xpress Kalis Mosel models. The module kalis extends the Mosel language with functionality for defining and solving Constraint Programming (CP) problems.

Prerequisites

This manual assumes some familiarity with the Mosel syntax. The reader is refered to the `Mosel User Guide' for an introduction to working with Mosel. The `Mosel Language Reference Manual' contains the complete documentation of the Mosel language. The `Getting Started' manual explains how to work with Mosel models in Xpress Workbench.