Modeling basics

Topics covered in this chapter:

This chapter shows how to

• start working with Mosel,
• create and solve a simple CP model using Xpress Kalis from Mosel,
• understand and analyze the output produced by the software,
• extend the model with data handling,
• define an objective function, and
• modify the default branching strategy.

A first model

Consider the following problem: we wish to schedule four meetings A, B, C, and D in three time slots (numbered 1 to 3). Some meetings are attended by the same persons, meaning that they may not take place at the same time: meeting A cannot be held at the same time as B or D, and meeting B cannot take the same time slot as C or D.

More formally, we may write down this problem as follows, where plan_m (m ∈ MEETINGS={A, B, C, D}) denotes the time slot for meeting m—these are the decision variables of our problem.

∀ m ∈ MEETINGS: plan_m ∈ {1,2,3}
plan_A ≠ plan_B
plan_A ≠ plan_D
plan_B ≠ plan_C
plan_B ≠ plan_D

Implementation with Mosel

The following code listing implements and solves the problem described above.

model "Meeting"
 uses "kalis"

 declarations
  MEETINGS = {'A','B','C','D'}        ! Set of meetings
  TIME = 1..3                         ! Set of time slots
  plan: array(MEETINGS) of cpvar      ! Time slot per meeting
 end-declarations

 forall(m in MEETINGS) setdomain(plan(m), TIME)

! Respect incompatibilities
 plan('A') <> plan('B')
 plan('A') <> plan('D')
 plan('B') <> plan('C')
 plan('B') <> plan('D')

! Solve the problem
 if not cp_find_next_sol then
  writeln("Problem is infeasible")
  exit(1)
 end-if

! Solution printing
 forall(m in MEETINGS)
  writeln("Meeting ", m, ": ", getsol(plan(m)))

end-model

This Mosel model is saved as a text file with the name meeting.mos. Let us now take a closer look at what we have just written.

General structure

Every Mosel program starts with the keyword model, followed by a model name chosen by the user. The Mosel program is terminated with the keyword end-model.

As Mosel is itself not a solver, we specify that the Kalis constraint solver is to be used with the statement

 uses "kalis"

at the begin of the model.

All objects must be declared in a declarations section, unless they are defined unambiguously through an assignment. For example, i:= 1 defines i as an integer and assigns to it the value 1. There may be several such declarations sections at different places in a model.

In the present case, we define two sets, and one array:

• MEETINGS is a set of strings.
• TIME is a so-called range set—i.e., a set of consecutive integers (here: from 1 to 3).
• plan is an array of decision variables of type cpvar (finite domain CP variables; a second decision variable type of kalis is cpfloatvar for continuous variables), indexed by the set MEETINGS.

The model then defines the domains of the variables using the kalis procedure setdomain. The decision variables are indeed created at their declaration with a large default domain and setdomain reduces these domains to the intersection of the default domain with the indicated values. As in the mathematical model, we use a forall loop to enumerate all the indices in the set MEETINGS.

This is followed by the statement of the constraints, in this model we have four disequality constraints.

Solving and solution output

With the function cp_find_next_sol, we call Kalis to solve the problem (find a feasible assignment of values to all decision variables). We test the return value of this function: if no solution is found it returns false and we stop the model execution at this point (by calling the Mosel procedure exit), otherwise we print out the solution.

To solve the problem Xpress Kalis uses its built-in default search strategies. We shall see later how to modify these strategies.

The solution for a CP variable is obtained with the function getsol. To write several items on a single line use write instead of writeln for printing the output.

Formatting

Indentation, spaces, and empty lines in our model have been added to increase readability. They are skipped by Mosel.

Line breaks: It is possible to place several statements on a single line, separating them by semicolons, as such:

 plan('A') <> plan('B'); plan('A') <> plan('D')

But since there are no special `line end' or continuation characters, every line of a statement that continues over several lines must end with an operator (+, >=, etc.) or characters like `,' that make it obvious that the statement is not terminated.

As shown in the example, single line comments in Mosel are preceded by !. Multiple line comments start with (! and terminate with !).

Running the model

You may choose among three different methods for running your Mosel models:

1. From the Mosel command line: this method can be used on all platforms for which Mosel is available. It is especially useful if you wish to execute a (batch) sequence of model runs—for instance, with different parameter settings. The full Mosel functionality, including its debugger, is accessible in this run mode.
2. Within the graphical environment Xpress Workbench: available to Windows users. Workbench is a complete modeling and optimization development environment with a built-in text editor for working with Mosel models and a number of displays that help analyze models and solution algorithms in the development phase. Models can be modified and re-run interactively.
3. From within an application program: Mosel models may be executed and accessed from application programs (C/C++, Java, VBA, C#). This functionality is typically used for the deployment of Mosel models, integrating them into a company's information system.

In this manual we shall use the first two methods for running the models we develop. For further detail on embedding models into application programs the user is referred to the Mosel User Guide.

Working from the Mosel command line

When you have entered the complete model into the file meeting.mos, we can proceed to the solution to our problem. We start Mosel at the command prompt by typing the following command

mosel execute meeting.mos

and we will see output something like that below.

Meeting A: 1 Meeting B: 2 Meeting C: 1 Meeting D: 3

The Mosel command for executing the model can be abbreviated to

mosel exec meeting

or simply

mosel meeting

The model execution performed by the command execute comprises three stages:

1. Compiling meeting.mos
2. Loading the compiled model
3. Running the model we have just loaded.

Instead of using execute, you may choose to explicitly generate the compiled model file chess.bim

mosel compile meeting.mos

followed by

mosel run meeting.bim

to load and run the compiled model.

Using Xpress Workbench

To execute the model file meeting.mos with Workbench you need to carry out the following steps.

• Start up Workbench: if you have followed the standard installation procedure for Xpress Workbench, start the program by double clicking the icon on the desktop or selecting Start » Programs » Xpress » Xpress Workbench. Otherwise, you may also start up Workbench by double clicking a model file (file with extension .mos).
• Open the model file by choosing File » Open. The model source is then displayed in the central window (the Workbench Editor).
• Click the Run button or, alternatively, choose menu entry Run for the desired model.

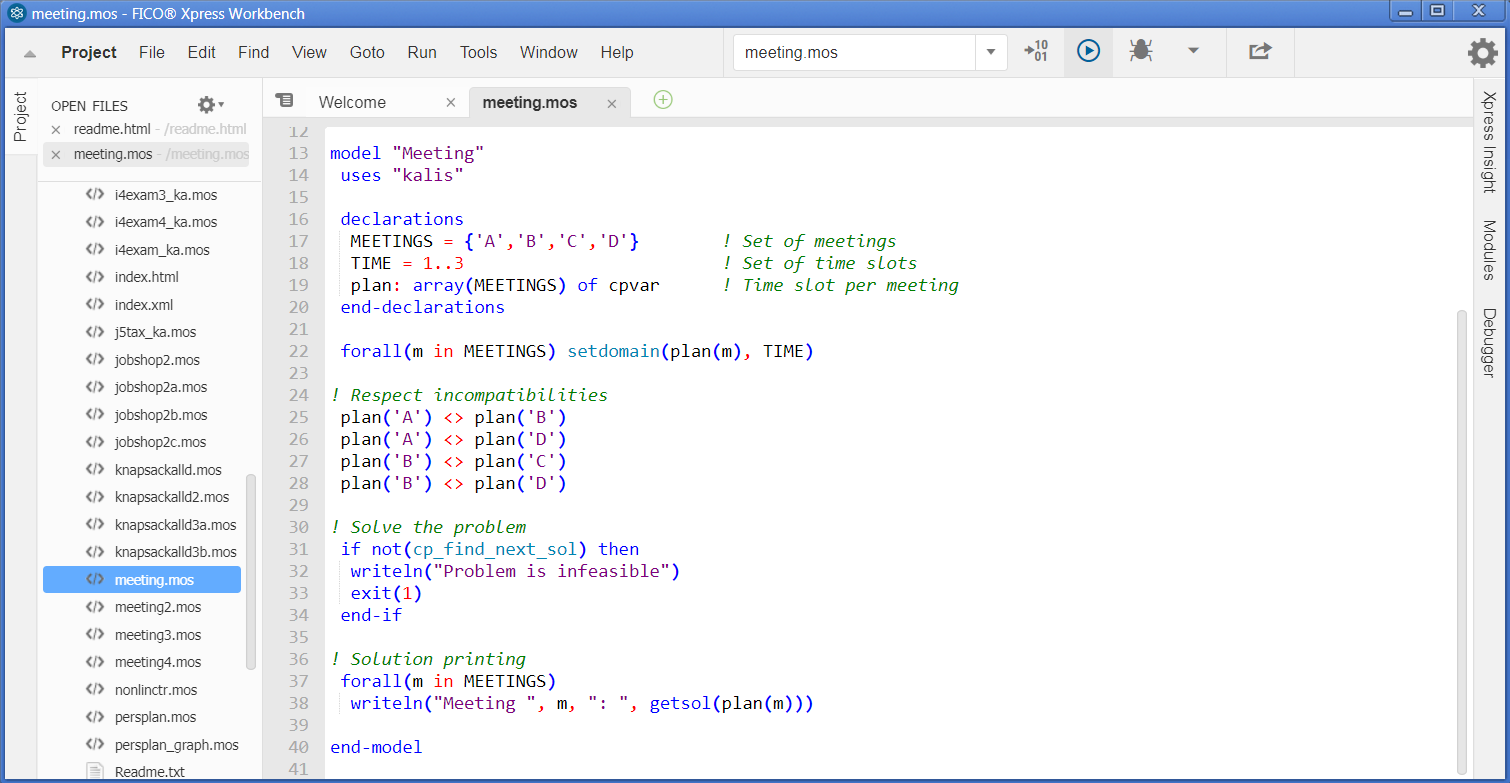
Figure 2.1: Workbench workspace after opening a model

The Build pane at the bottom of the workspace displays the model execution status messages from Mosel and any output generated by it. If syntax errors are found in the model they are displayed here, with details of the line and character position where the error was detected and a description of the problem, if available.

Workbench makes all information about the model available for inspection through the Debugger pane in the right hand window if the model is run in debug mode (bug icon ).

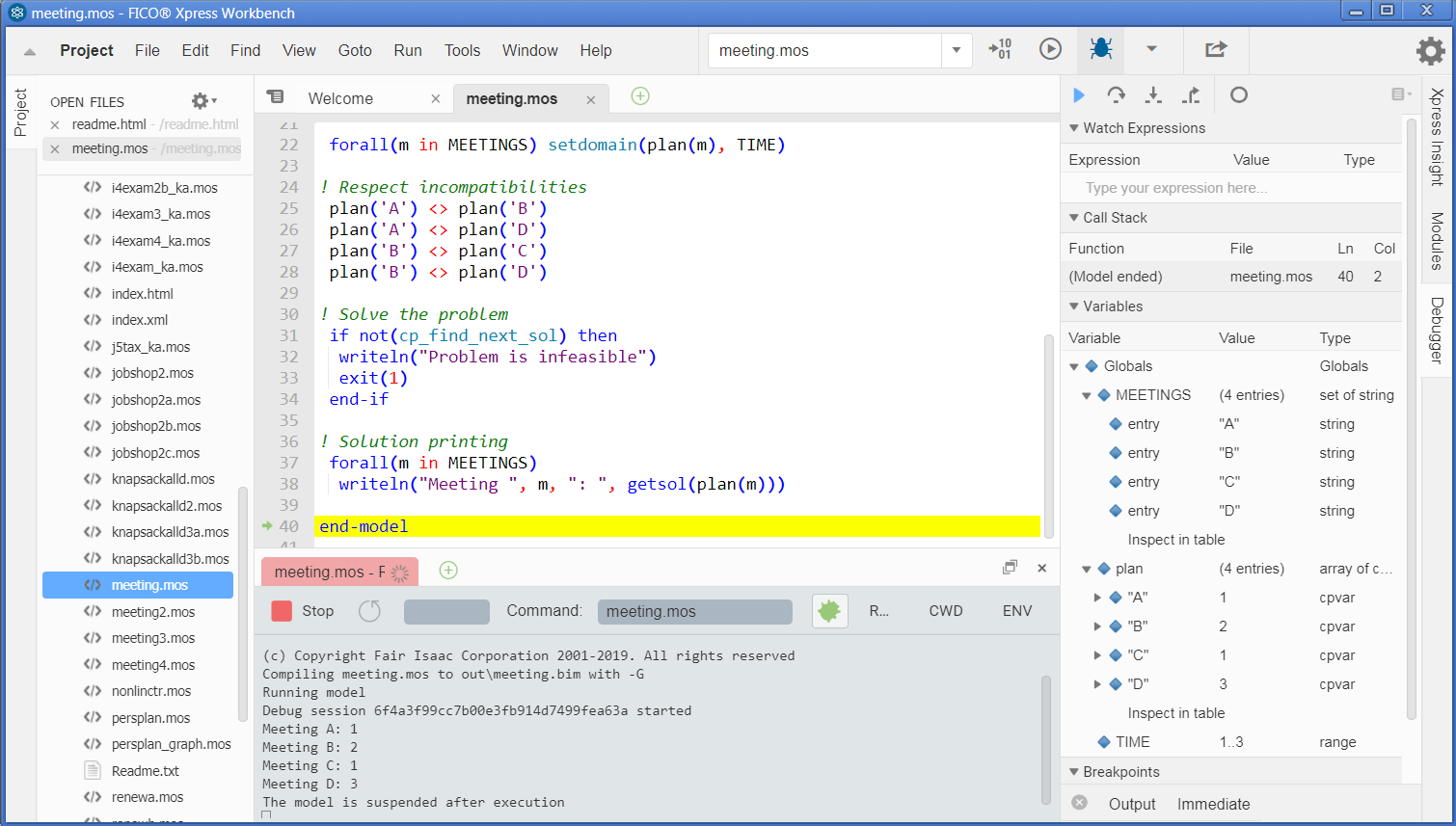
Figure 2.2: Workbench workspace after model execution in debug mode

Debugging a model

A first step for debugging a model certainly is to add additional output. In our model, we could, for instance, print out the definition of the decision variables by adding the line

 writeln(plan)

after the definition of the variables' domains, or even print out the complete problem definition with the procedure cp_show_prob. To obtain a more easily readable output for debugging the user may give names to the decision variables of his problem. For example:

 forall(m in MEETINGS) setname(plan(m), "Meeting "+m) 

Notice that we have used the '+' sign to concatenate strings.

Calling the procedure cp_show_stats will display summary statistics of the CP solving.

To obtain detailed information about run-time errors with the command line version models need to be compiled with the flag -g, for example,

mosel exec -g meeting

For using the Mosel debugger (please see the Mosel Language Reference Manual for further detail) the compilation flag -G needs to be used instead.

Workbench by default compiles models in standard mode, debug+trace information (option -G) is automatically enabled when launching a debugging run (the debugger is started by clicking the 'debug' button or via the Debug entry of the Run menu).

Data input from file

We now extend the previous example in order to use it with different data sets. If we wish to run a model with different data sets, it would be impractical and error-prone having to edit the model file with every change of the data set. Instead, we are now going to see how to read data from a text file.

This is a description of the problem we want to solve (example taken from Section 14.4 of the book `Applications of optimization with Xpress-MP').

A technical university needs to schedule the exams at the end of the term for a course with several optional modules. Every exam lasts two hours. Two days have been reserved for the exams with the following time periods: 8:00–10:00, 10:15–12:15, 14:00–16:00, and 16:15–18:15, resulting in a total of eight time periods. For every exam the set of incompatible exams that may not take place at the same time because they have to be taken by the same students is shown in Table Incompatibilities between different exams.

Table 2.1: Incompatibilities between different exams

	DA	NA	C++	SE	PM	J	GMA	LP	MP	S	DSE
DA	–	X	–	–	X	–	X	–	–	X	X
NA	X	–	–	–	X	–	X	–	–	X	X
C++	–	–	–	X	X	X	X	–	X	X	X
SE	–	–	X	–	X	X	X	–	–	X	X
PM	X	X	X	X	–	X	X	X	X	X	X
J	–	–	X	X	X	–	X	–	X	X	X
GMA	X	X	X	X	X	X	–	X	X	X	X
LP	–	–	–	–	X	–	X	–	–	X	X
MP	–	–	X	–	X	X	X	–	–	X	X
S	X	X	X	X	X	X	X	X	X	–	X
DSE	X	X	X	X	X	X	X	X	X	X	–

Model formulation

The CP model has the same structure as the previous one, with the difference that we now introduce a data array INCOMP indicating incompatible pairs of exams and define the disequality constraints in a loop instead of writing them out one by one.

∀ e ∈ EXAM: plan_e ∈ {1,...,8}
∀ d,e ∈ EXAM, INCOMP_de=1: plan_d ≠ plan_e

Implementation

The Mosel model now looks as follows.

model "I-4 Scheduling exams (CP)"
 uses "kalis"

 declarations
  EXAM = 1..11                        ! Set of exams
  TIME = 1..8                         ! Set of time slots
  INCOMP: array(EXAM,EXAM) of integer ! Incompatibility between exams
  EXAMNAME: array(EXAM) of string

  plan: array(EXAM) of cpvar          ! Time slot for exam
 end-declarations

 EXAMNAME:: (1..11)["DA","NA","C++","SE","PM","J","GMA","LP","MP","S","DSE"]

 initializations from 'Data/i4exam.dat'
  INCOMP
 end-initializations

 forall(e in EXAM) setdomain(plan(e), TIME)

! Respect incompatibilities
 forall(d,e in EXAM | d<e and INCOMP(d,e)=1)  plan(d) <> plan(e)

! Solve the problem
 if not cp_find_next_sol then
  writeln("Problem is infeasible")
  exit(1)
 end-if

! Solution printing
 forall(t in TIME) do
  write("Slot ", t, ": ")
  forall(e in EXAM | getsol(plan(e))=t) write(EXAMNAME(e)," ")
  writeln
 end-do

end-model

The values of the array INCOMP are read in from the file i4exam.dat in an initializations block. In the definition of the disequality constraints we check the value of the corresponding array entry—conditions on the indices for loops, sums, and other aggregate operators are marked by a vertical bar.

The data file has the following contents.

INCOMP: [0 1 0 0 1 0 1 0 0 1 1
         1 0 0 0 1 0 1 0 0 1 1
         0 0 0 1 1 1 1 0 1 1 1
         0 0 1 0 1 1 1 0 0 1 1
         1 1 1 1 0 1 1 1 1 1 1
         0 0 1 1 1 0 1 0 1 1 1
         1 1 1 1 1 1 0 1 1 1 1
         0 0 0 0 1 0 1 0 0 1 1
         0 0 1 0 1 1 1 0 0 1 1
         1 1 1 1 1 1 1 1 1 0 1
         1 1 1 1 1 1 1 1 1 1 0]

Results

The model prints out the following results. Only the first seven time slots are used for scheduling exams.

Slot 1: DA C++ LP
Slot 2: NA SE MP
Slot 3: PM
Slot 4: GMA
Slot 5: S
Slot 6: DSE
Slot 7: J
Slot 8: 

Data-driven model

In the model shown above, we have read the incompatibility data from a file but part of the data (namely the index set EXAM and the number of time slots available) are still hard-coded in the model. To obtain a fully flexible model that can be run with arbitrary data sets we need to move all data definitions from the model to the data file.

The new data file i4exam2.dat not only defines the data entries, it also defines the index tuples for the array INCOMP. Every data entry is preceded by its index tuple (in brackets). There is no need to write out explicitly the contents of the set EXAM—Mosel will automatically populate this set with the index values read in for the array INCOMP. In addition, the data file now contains a value for the number of time periods NT.

INCOMP: [("DA" "NA") 1 ("DA" "PM") 1 ("DA" "GMA") 1 ("DA" "S") 1 ("DA" "DSE") 1
         ("NA" "DA") 1 ("NA" "PM") 1 ("NA" "GMA") 1 ("NA" "S") 1 ("NA" "DSE") 1
         ("C++" "SE") 1 ("C++" "PM") 1 ("C++" "J") 1 ("C++" "GMA") 1
	 ("C++" "MP") 1 ("C++" "S") 1 ("C++" "DSE") 1
         ("SE" "C++") 1 ("SE" "PM") 1 ("SE" "J") 1 ("SE" "GMA") 1 ("SE" "S") 1
	 ("SE" "DSE") 1
         ("PM" "DA") 1 ("PM" "NA") 1 ("PM" "C++") 1 ("PM" "SE") 1 ("PM" "J") 1
	 ("PM" "GMA") 1 ("PM" "LP") 1 ("PM" "MP") 1 ("PM" "S") 1 ("PM" "DSE") 1
         ("J" "C++") 1 ("J" "SE") 1 ("J" "PM") 1 ("J" "GMA") 1 ("J" "MP") 1
	 ("J" "S") 1 ("J" "DSE") 1
         ("GMA" "DA") 1 ("GMA" "NA") 1 ("GMA" "C++") 1 ("GMA" "SE") 1
	 ("GMA" "PM") 1 ("GMA" "J") 1 ("GMA" "LP") 1 ("GMA" "MP") 1
	 ("GMA" "S") 1 ("GMA" "DSE") 1
         ("LP" "PM") 1 ("LP" "GMA") 1 ("LP" "S") 1 ("LP" "DSE") 1
         ("MP" "C++") 1 ("MP" "PM") 1 ("MP" "J") 1 ("MP" "GMA") 1 ("MP" "S") 1
	 ("MP" "DSE") 1
         ("S" "DA") 1 ("S" "NA") 1 ("S" "C++") 1 ("S" "SE") 1 ("S" "PM") 1
	 ("S" "J") 1 ("S" "GMA") 1 ("S" "LP") 1 ("S" "MP") 1 ("S" "DSE") 1
         ("DSE" "DA") 1 ("DSE" "NA") 1 ("DSE" "C++") 1 ("DSE" "SE") 1
	 ("DSE" "PM") 1 ("DSE" "J") 1 ("DSE" "GMA") 1 ("DSE" "LP") 1
	 ("DSE" "MP") 1 ("DSE" "S") 1 ]

NT: 8

Our model also needs to undergo a few changes: the sets EXAM and TIME are now declared by stating their types, which turns them into dynamic sets (as opposed to their previous constant definition by stating their values). As a consequence, the array of decision variables plan is declared before the indexing set EXAM is known and Mosel creates this array as a dynamic array, meaning that the declaration results in an empty array and its elements need to be created explicitly (using the Mosel procedure create) once the indices are known. Before creating the variables, we modify the default bounds of Xpress Kalis to the values corresponding to the set TIME, thus replacing the call to setdomain.

The array INCOMP is explicitly declared as a dynamic array. The initializations block will assign values to just those entries that are listed in the data file (with the previous, constant declaration, all entries were defined) and the explicit dynamic marker means that Mosel's automatic finalization is not applied—it would try to transform the array into a static array. This makes it possible to reformulate the condition on the loop defining the disequality constraints: we now simply test for the existence of an entry instead of comparing all data values. With larger data sets, using the keyword exists may greatly reduce the execution time of loops involving sparse arrays (multidimensional data arrays with few entries different from 0).

model "I-4 Scheduling exams (CP) - 2"
 uses "kalis"

 declarations
  NT: integer                         ! Number of time slots
  EXAM: set of string                 ! Set of exams
  TIME: set of integer                ! Set of time slots
  INCOMP: dynamic array(EXAM,EXAM) of integer ! Incompatibility between exams

  plan: array(EXAM) of cpvar          ! Time slot for exam
 end-declarations

 initializations from 'Data/i4exam2.dat'
  INCOMP NT
 end-initializations

 TIME:= 1..NT

 setparam("kalis_default_lb", 1); setparam("kalis_default_ub", NT)
 forall(e in EXAM) create(plan(e))

! Respect incompatibilities
 forall(d,e in EXAM | exists(INCOMP(d,e)) and d<e)  plan(d) <> plan(e)

! Solve the problem
 if not cp_find_next_sol then
  writeln("Problem is infeasible")
  exit(1)
 end-if

! Solution printing
 forall(t in TIME) do
  write("Slot ", t, ": ")
  forall(e in EXAM | getsol(plan(e))=t) write(e," ")
  writeln
 end-do

end-model

Running this fully data-driven model produces the same solution as the previous version.

An alternative to the explicit creation of the decision variables plan is to move their declaration after the initialization of the data as shown in the code extract below. In this case, it is important to finalize the indexing set EXAM, which turns it into a constant set with its current contents and allows Mosel to create any subsequently declared arrays indexed by this set as static arrays.

 declarations
  NT: integer                         ! Number of time slots
  EXAM: set of string                 ! Set of exams
  TIME: set of integer                ! Set of time slots
  INCOMP: dynamic array(EXAM,EXAM) of integer ! Incompatibility between exams
 end-declarations

 initializations from 'Data/i4exam2.dat'
  INCOMP NT
 end-initializations

 finalize(EXAM)
 TIME:= 1..NT

 setparam("kalis_default_lb", 1); setparam("kalis_default_ub", NT)
 declarations
  plan: array(EXAM) of cpvar          ! Time slot for exam
 end-declarations 

Optimization and enumeration

Optimization

Since running our model i4exam_ka.mos in Section Implementation has produced a solution to the problem that does not use all time slots one might wonder which is the minimum number of time slots that are required for this problem. This question leads us to the formulation of an optimization problem.

We introduce a new decision variable numslot over the same value range as the plan_i variables and add the constraints that this variable is greater or equal to every plan_i variable. A simplified formulation is to say that the variable numslot equals the maximum value of all plan_i variables.

The objective then is to minimize the value of numslot, which results in the following model.

model "I-4 Scheduling exams (CP) - 3"
 uses "kalis"

 declarations
  NT: integer                         ! Number of time slots
  EXAM: set of string                 ! Set of exams
  TIME: set of integer                ! Set of time slots
  INCOMP: dynamic array(EXAM,EXAM) of integer ! Incompatibility between exams

  plan: array(EXAM) of cpvar          ! Time slot for exam
  numslot: cpvar                      ! Number of time slots used
 end-declarations

 initializations from 'Data/i4exam2.dat'
  INCOMP NT
 end-initializations

 finalize(EXAM)
 TIME:= 1..NT

 setparam("kalis_default_lb", 1); setparam("kalis_default_ub", NT)
 forall(e in EXAM) create(plan(e))

! Respect incompatibilities
 forall(d,e in EXAM | exists(INCOMP(d,e)) and d<e)  plan(d) <> plan(e)

! Calculate number of time slots used
 numslot = maximum(plan)

! Solve the problem
 if not cp_minimize(numslot) then
  writeln("Problem is infeasible")
  exit(1)
 end-if

! Solution printing
 forall(t in TIME) do
  write("Slot ", t, ": ")
  forall(e in EXAM | getsol(plan(e))=t) write(e," ")
  writeln
 end-do

end-model

Instead of cp_find_next_sol we now use cp_minimize with the objective function variable numslot as function argument.

This program also generates a solution using seven time slots, thus proving that this is the least number of slots required to produce a feasible schedule.

Enumeration

When comparing the problem statistics obtained by adding a call to cp_show_stats to the end of the different versions of our model, we can see that switching from finding a feasible solution to optimization considerably increases the number of nodes explored by the CP solver.

So far we have simply relied on the default enumeration strategies of Xpress Kalis. We shall now try to see whether we can reduce the number of nodes explored and hence shorten the time spent by the search for proving optimality.

The default strategy of Kalis for enumerating finite domain variables corresponds to adding the statement

cp_set_branching(assign_var(KALIS_SMALLEST_DOMAIN, KALIS_MIN_TO_MAX)) 

before the start of the search. assign_var denotes the branching scheme (`a branch is formed by assigning the next chosen value to the branching variable'), KALIS_SMALLEST_DOMAIN is the variable selection strategy (`choose the variable with the smallest number of values remaining in its domain'), and KALIS_MIN_TO_MAX the value selection strategy (`from smallest to largest value').

Since we are minimizing the number of time slots, enumeration starting with the smallest value seems to be a good idea. We therefore keep the default value selection criterion. However, we may try to change the variable selection heuristic: replacing KALIS_SMALLEST_DOMAIN by KALIS_MAX_DEGREE results in a reduction of the tree size and search time to less than half of its default size.

Here follows once more the complete model.

model "I-4 Scheduling exams (CP) - 4"
 uses "kalis"

 declarations
  NT: integer                         ! Number of time slots
  EXAM: set of string                 ! Set of exams
  TIME: set of integer                ! Set of time slots
  INCOMP: dynamic array(EXAM,EXAM) of integer ! Incompatibility between exams

  plan: array(EXAM) of cpvar          ! Time slot for exam
  numslot: cpvar                      ! Number of time slots used
 end-declarations

 initializations from 'Data/i4exam2.dat'
  INCOMP NT
 end-initializations

 finalize(EXAM)
 TIME:= 1..NT

 setparam("kalis_default_lb", 1); setparam("kalis_default_ub", NT)
 forall(e in EXAM) create(plan(e))

! Respect incompatibilities
 forall(d,e in EXAM | exists(INCOMP(d,e)) and d<e)  plan(d) <> plan(e)

! Calculate number of time slots used
 numslot = maximum(plan)

! Setting parameters of the enumeration
 cp_set_branching(assign_var(KALIS_MAX_DEGREE, KALIS_MIN_TO_MAX))

! Solve the problem
 if not cp_minimize(numslot) then
  writeln("Problem is infeasible")
  exit(1)
 end-if

! Solution printing
 forall(t in TIME) do
  write("Slot ", t, ": ")
  forall(e in EXAM | getsol(plan(e))=t) write(e," ")
  writeln
 end-do

 cp_show_stats

end-model

NB: In the model versions without optimization we may try to obtain a more evenly distributed schedule by choosing values randomly, that is, by using the value selection criterion KALIS_RANDOM_VALUE instead of KALIS_MIN_TO_MAX.

Further detail on the definition of branching strategies is given in Chapter Enumeration.

Continuous variables

All through this chapter we have worked with the decision variable type cpvar (discrete variables). A second variable type in Xpress Kalis are continuous variables (Mosel type cpfloatvar). Such variables are used in a similar way to what we have seen above for discrete variables, for example:

 setparam("KALIS_DEFAULT_CONTINUOUS_LB", 0)
 setparam("KALIS_DEFAULT_CONTINUOUS_UB", 10)

 declarations
  x,y: cpfloatvar
 end-declarations

 x >= y                   ! Define a constraint
                          ! Retrieve information about continuous variables
 writeln(getname(x), ":", getsol(x))
 writeln(getlb(y), " ", getub(y)) 

A few differences in the use of the two decision variable types exist:

• Constraints involving cpfloatvar cannot be strict inequalities (that is, only the operators <=, >=, and = may be used).
• Most global constraints (see Chapter Constraints) only apply to cpvar; also applicable to cpfloatvar are maximum and minimum relations.
• Search strategies enumerating the values in a variable's domain can only be used with cpvar; with cpfloatvar domain splitting must be used (see Chapter Enumeration).
• Access functions for enumerating domain values such getnext are not applicable to cpfloatvar.