Nonlinear Problems

Topics covered in this chapter:

Xpress NonLinear will solve nonlinear problems. In this context, a nonlinear problem is one in which there are nonlinear relationships between variables or where there are nonlinear terms in the objective function. There is no such thing as a nonlinear variable — all variables are effectively the same — but there are nonlinear constraints and formulae. A nonlinear constraint contains terms which are not linear. A nonlinear term is one which is not a constant and is not a variable with a constant coefficient. A nonlinear constraint can contain any number of nonlinear terms.

Xpress NonLinear will also solve linear problems — that is, if the problem presented to Xpress NonLinear does not contain any nonlinear terms, then Xpress NonLinear will still solve it, using the normal optimizer library.

The solution mechanism used by Xpress-SLP is Successive (or Sequential) Linear Programming. This involves building a linear approximation to the original nonlinear problem, solving this approximation (to an optimal solution) and attempting to validate the result against the original problem. If the linear optimal solution is sufficiently close to a solution to the original problem, then the SLP is said to have converged, and the procedure stops. Otherwise, a new approximation is created and the process is repeated. Xpress-SLP has a number of features which help to create good approximations to the original problem and therefore help to produce a rapid solution.

When licensed, Xpress NonLinear may also utilize Knitro to solve nonlinear problems.

Note that although the solution is the result of an optimization of the linear approximation, there is no guarantee that it will be an optimal solution to the original nonlinear problem. It may be a local optimum — that is, it is a better solution than any points in its immediate neighborhood, but there is a better solution rather further away. However, a converged SLP solution will always be (to within defined tolerances) a self-consistent — and therefore practical — solution to the original problem.

Coefficients and formulas

Later in this manual, it will be helpful to distinguish between nonlinear expressions written as coefficients and those written as formulas.

If X is a variable, then in the nonlinear expression X*f(Y), f(Y) is the coefficient of X.

If f(X) appears in a nonlinear constraint, then f(X) is a nonlinear formula in the nonlinear constraint.

If X*f(Y) appears in a nonlinear constraint, then the entity X*f(Y) is a term in the nonlinear constraint.

As this implies, a formula written as a variable multiplied by a coefficient can always be viewed as a term, but there are terms which cannot be viewed as variables multiplied by coefficients. For example, in the constraint
X - SIN(Y) = 0,
SIN(Y) is a formula and cannot be written as a coefficient.

SLP variables

A variable which appears in a nonlinear coefficient or formula is described as an SLP variable.

Normally, any variable which has a nonlinear coefficient will also be treated as an SLP variable. However, it is possible to set options so that variables which do not appear in nonlinear coefficients or formulas are not treated as SLP variables.

Any variable, whether it is related to a nonlinear formula or not, can be defined by the user as an SLP variable. This is most easily achieved by setting an initial value for the variable.

Local and global optimality

A globally optimal solution is a feasible solution with the best objective value among all feasible solutions for an optimization problem. In contrast, a locally optimal solution only has the best objective value within a limited neighborhood surrounding it. It's important to note that better solutions may exist in different regions of the problem space. While for convex problems every local optimum is a global optimum, this is not the case for general nonlinear problems.

The FICO Xpress library offers solvers that provide global optima for both convex and nonconvex problems. The base offering includes solving linear, quadratic, and quadratically constrained problems, as well as their mixed-integer counterparts. To handle more general nonlinear problems, a license for FICO Xpress Global is required.

For black-box optimization or obtaining local optima with duals for continuous nonlinear problems, a license for FICO Xpress Nonlinear is necessary. FICO Xpress Nonlinear can also be used as a heuristic for mixed-integer nonlinear problems. It's important to note that finding a local optimum is usually much faster than finding a global optimum, but using a local solver doesn't provide guarantees on the global quality of the solution and may encounter issues such as local infeasibilities.

Lastly, neither local nor global optima are typically unique. The solution returned by a solver depends on the control settings and, especially for non-convex problems, the initial values provided. A connected set of initial points that yield the same locally optimal solutions is referred to as a region of attraction. These regions are algorithm and setting dependent.

Convexity

Convex problems have many desirable characteristics from the perspective of mathematical optimization. Perhaps the most significant of these is that should both the objective and the feasible region be convex, any local optimally solutions found are also known immediately to be globally optimal.

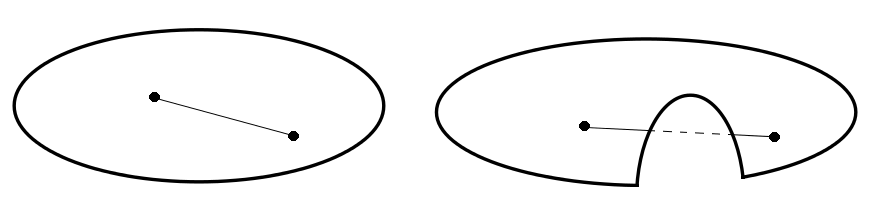
A constraint f(x)≤0 is convex if the matrix of second derivatives of f, that is to say its Hessian, is positive semi-definite at every point at which it exists. This requirement can be understood geometrically as requiring every point on every line segment which connects two points satisfying the constraint to also satisfy the constraint. It follows trivially that linear functions always lead to convex constraints, and that a nonlinear equality constraint is never convex.

Figure 6.1: Two convex functions on the left, and two non-convex functions on the right.

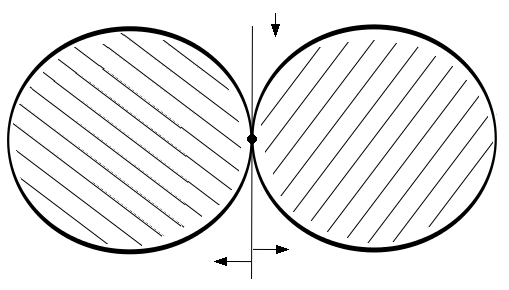
For regions, a similar property must hold. If any two points of the region can be connected by a line segment which lies fully in the region itself, the region is convex. This extension is straightforward when the the properties of convex functions are considered.

Figure 6.2: A convex region on the left and a non-convex region on the right.

It is important to note that convexity is necessary for some solution techniques and not for others. In particular, some solvers require convexity of the constraints and objective function to hold only in the feasible region, whilst others may require convexity to hold across the entire space, including infeasible points. In the special case of quadratic and quadratically constrained programs, Xpress NonLinear seamlessly migrates problems to solvers whose convexity requirements match the convexity of the problem.

Converged and practical solutions

In a strict mathematical sense, an algorithm is said to have converged if repeated iterations do not alter the coordinates of its solution significantly. A more practical view of convergence, as used in the nonlinear solvers of the Xpress suite, is to also consider the algorithm to have converged if repeated iterations have no significant effect on either the objective value or upon feasibility. This will be called extended convergence to distinguish it from the strict sense.

For some problems, a solver may visit points at which the local neighborhood is very complex, or even malformed due to numerical issues. In this situation, the best results may be obtained when convergence of some of the variables is forced. This leads to practical solutions, which are feasible and converged in most variables, but the remaining variables have had their convergence forced by the solver, for example by means of a trust region. Although these solutions are not locally optimal in a strict sense, they provide meaningful, useful results for difficult problems in practice.

The duals of general, nonlinear program

The dual of a mathematical program plays a fundamental role in the theory of continuous optimization. Each variable in a problem has a corresponding partner in that problem's dual, and the values of those variables are called the reduced costs and dual multipliers (shadow prices). Xpress NonLinear makes estimates of these values available. These are normally defined in a similar way to the usual linear programming case, so that each value represents the rate of change of the objective when either increasing the corresponding primal variable or relaxing the corresponding primal constraint.

From an algorithmic perspective, one of the most important roles of the dual variables is to characterize local optimality. In this context, the dual multipliers and reduced costs are called Lagrange multipliers, and a solution with both primal and dual feasible variables satisfies the Karush-Kuhn-Tucker conditions. However, it is important to note that for general nonlinear problems, there exist situations in which there are no such multipliers. Geometrically, this means that the slope of the objective function is orthogonal to the linearization of the active constraints, but that their curvature still prevents any movement in the improving direction.

As a simple example, consider:

minimize	y
subject to	x2 + y2 ≤ 1
	(x-2)2 + y2 ≤ 1

which is shown graphically in figure A problem admitting no dual values.

Figure 6.3: A problem admitting no dual values

This problem has a single feasible solution at (1,0). Reduced costs and dual multipliers could never be meaningful indicators of optimality, and indeed are not well-defined for this problem. Intuitively, this arises because the feasible region lacks an interior, and the existence of an interior (also referred to as the Slater condition) is one of several alternative conditions which can be enforced to ensure that such situations do not occur. The other common condition for well-defined duals is that the gradients of the active constraints are linearly independent.

Problems without valid duals do not often arise in practice, but it is important to be aware of the possibility. Analytic detection of such issues is difficult, and they manifest instead in the form of unexpectedly large or otherwise implausible dual values.