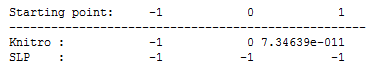Xpress-SLP Solution Process
Topics covered in this chapter:
This section gives a brief overview of the sequence of operations within Xpress-SLP once the data has been set up. The positions of the possible user callbacks are also shown.
| Check if problem is an SLP problem or not. Call the appropriate XPRS library function if not, and DONE. [Call out to user callback if set by XSLPsetcbslpstart] Augment the matrix (create the linearized structure) if not already done If determining row data supplied, calculate cascading order and detect determining columns DO [Call out to user callback if set by XSLPsetcbiterstart] If previous solution available, pre-process solution Execute line search [Call out to user callback if set by XSLPsetcbcascadestart] Sequentially update values of SLP variables (cascading) and re-calculate coefficients For each variable (in a suitable evaluation order): Update solution value (cascading) and re-calculate coefficients [Call out to user callback if set by XSLPsetcbcascadevar] [Call out to user callback if set by XSLPsetcbcascadeend] Update penalties Update coefficients, bounds and RHS in linearized matrix Solve linearized problem using the Xpress Optimizer Recover SLP variable and delta solution values Test convergence against specified tolerances and other criteria For each variable: Test convergence against specified tolerances [Call out to user callback if set by XSLPsetcbitervar] For each variable with a determining column: Check value of determining column and fix variable when necessary, or [Call out to user callback if set by XSLPsetcbdrcol] Reset variable convergence status if a change is made to a variable If not all variables have converged, check for other extended convergence criteria If the solution has converged, then BREAK For each SLP variable: Update history Reset step bounds [Call out to user callback if set by XSLPsetcbiterend] Change row types for DC rows as required If SLP iteration limit is reached, then BREAK END DO [Call out to user callback if set by XSLPsetcbslpend] |
For MISLP (mixed-integer SLP) problems, the above solution process is normally repeated at each node. The standard procedure for each node is as follows:
| Initialize node [Call out to user callback if set by XSLPsetcbprenode] Solve node using SLP procedure If an optimal solution is obtained for the node then [Call out to user callback if set by XSLPsetcboptnode] If an integer optimal solution is obtained for the node then [Call out to user callback if set by XSLPsetcbintsol] When node is completed [Call out to user callback if set by XSLPsetcbslpnode] |
When a problem is destroyed, there is a call out to the user callback set by XSLPsetcbdestroy.
Analyzing the solution process
Xpress-SLP provides a comprehensive set of callbacks to interact with, and to analyze the solution process. However, there are a set of purpose build options that are intended to assist and make the analysis more efficient.
For infeasible problems, it often helps to identify the source of conflict by running XPRESS' Irreducible Infeasibiliy Set (IIS) finder tool. The set found by IIS often helps to either point to a problem in the original model formulation, or if the infeasibility is a result of conflicting step bounds or linearization updates; please see control XSLP_ANALYZE.
It is often advantageous to trace a certain variable, constraint or a certain property through the solution process. XSLP_TRACEMASK and XSLP_TRACEMASKOPS allows for collecting detailed information during the solution process, without the need to stop XSLP between iterations.
For in depth debugging purposes or support requests, it is possible to create XSLP save files and linearizations at verious iterations, controlled by XSLP_AUTOSAVE and XSLP_ANALYZE.
The initial point
The solution process is sensitive to the initial values which are selected for variables in the problem, and particularly so for non-convex problems. It is not uncommon for a general nonlinear problem to have a feasible region which is not connected, and in this case the starting point may largely determine which region, connected set, or basin of attraction the final solution belongs to.
Note that it may not always be beneficial to completely specify an initial point, as the solvers themselves may be able to detect suitable starting values for some or all of the variables.
Derivatives
Both XSLP and Knitro require the availability of derivative information for the constraints and objective function in order to solve a problem. In the Xpress NonLinear framework, several advanced approaches to the production of both first and second order derivatives (the Jacobian and Hessian matrices) are available, and which approach is used can be controlled by the user.
Finite Differences
The simplest such method is the use of finite differences, sometimes called numerical derivatives. This is a relatively coarse approximation, in which the function is evaluated in a small neighborhood of the point in question. The standard argument from calculus indicates that an increasingly accurate approximation to the derivative of the function will be found as the size of the neighborhood decreases. This argument ignores the effects of floating point arithmetic, however, which can make it difficult to select values sufficiently small to give a good approximation to the function, and yet sufficiently large to avoid substantial numerical error.
The high performance implementation in XSLP makes use of subexpression caching to improve performance, but finite differences are inherently inefficient. They may however be necessary when the function itself is not known in closed form. When analytic approaches cannot be used, due to the use of expensive black box functions which do not provide derivatives (note that XSLP does allow user functions to provide their own derivatives), the cost of function evaluations may become a dominant factor in solve time. It is important to note that each second order numerical derivative costs twice as much as a first order numerical derivative, and this can make XSLP more attractive than Knitro for such problems.
Symbolic Differentiation
Xpress NonLinear will instead provide analytic derivatives where possible, which are both more accurate and more efficient. There are two major approaches to such calculations, and high quality implementations of both are available in this framework. A symbolic differentiation engine calculates the derivative of an expression in closed form, using its formula representation. This is a very efficient way of recalculating individual entries of the Jacobian, and is the default approach to providing derivative information to XSLP in case the total size of all derivatives is expected to fit into memory.Automatic Differentiation
An automatic differentiation engine in contrast can simultaneously compute multiple derivatives by repeated application of the chain rule. This is a very efficient means of calculating large numbers of Hessian entries, and is the default approach to providing derivative information to Knitro. It is also the default choice for SLP in case of large scale models.
Points of inflection
A point of inflection in a given variable occurs when the first and second order partial derivatives with respect to that variable become zero, but there exist nonzero derivatives of higher order. At such points, the approximations the iterative nonlinear methods create do not encapsulate enough information about the behavior of the function, and both first and second order methods may experience difficulties. For example, consider the following problem
| minimize | x3 |
| subject to | -1≤x≤1 |
When the initial value of x is varied, XSLP and Knitro produce the solutions presented in Table Effect of an inflection point on solution values. for this problem:
Figure 8.1: Effect of an inflection point on solution values.
As a second order method, Knitro examines a local quadratic approximation to the function. Starting at both 0 and 1, this approximation will closely resemble the x^2 function, and so the solution will be attracted to zero. For XSLP, which is a first order method, the approximation at 0 will have a zero gradient. However, XSLP can detect this situation and will perform the analysis required to substitute an appropriate small nonzero (placeholder) value for the derivative during the first iterations. As can be seen, this allows XSLP find an optimal solution in all three cases.
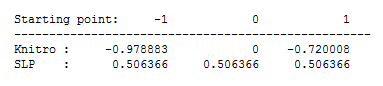
This is only one example of the behaviour of these solvers without further tuning. The long steps which XSLP often takes can be both beneficial and harmful in different contexts. For example, if the function to be optimized includes many local minima, it is possible to see the opposite pattern for XSLP and Knitro. Consider
| minimize | x |
| subject to | -1≤x≤1 |
Figure 8.2: Local solutions for a function with several local optima
In this case the same long steps made by XSLP lead to it finding the an identical, but unfortunate, local optimum no matter which initial point it begins from.
Trust regions
In a second order method like Knitro, there is a well-defined merit function which can be used to compare solutions, and which provides a measure of the progress being made by the algorithm. This is a significant advantage over first order methods, in which there is generally no such function.
Despite their speed and resilience to points of inflection, first order methods can also experience difficulties at points in which the current approximation is not well posed. Consider
| minimize | x2 |
| subject to | x free |
| minimize | 2x |
| subject to | x free |
© 2001-2024 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.