Problem Types
Topics covered in this chapter:
- Linear Programs (LPs)
- Mixed Integer Programs (MIPs)
- Quadratic Programs (QPs)
- Quadratically Constrained Quadratic Programs (QCQPs)
- Second Order Cone problems (SOCPs)
The FICO Xpress Optimization Suite is a powerful optimization tool for solving Mathematical Programming problems. Users of FICO Xpress formulate real-world problems as Mathematical Programming problems by defining a set of decision variables, a set of constraints on these variables and an objective function of the variables that should be maximized or minimized. Our FICO Xpress users have applications that define and solve important Mathematical Programming problems in academia and industry, including areas such as production scheduling, transportation, supply chain management, telecommunications, finance and personnel planning.
Mathematical Programming problems are usually classified according to the types of decision variables, constraints and objective function in the problem. Perhaps the most popular application of the FICO Xpress Optimizer is for the class of Mixed Integer Programs (MIPs). In this section we will briefly introduce some important types of problem that can be solved by the FICO Xpress Optimizer.
This section does not discuss general nonlinear problems. To solve such problems see FICO Xpress Nonlinear and FICO Xpress Global. Note that solving non-convex quadratically-constrained quadratic problems is included in the Xpress Optimizer license, whereas for general nonlinear problems, you need a license for either FICO Xpress Global or FICO Xpress Nonlinear.
Linear Programs (LPs)
Linear Programming (LP) problems are a very common type of optimization problems. In this type of problem all constraints and the objective function are linear expressions of the decision variables. Each decision variable is restricted to some continuous interval (typically non-negative). Although the methods for solving these types of problems are well known (e.g., the simplex method), only a few efficient implementations of these methods (and additional specialized methods for particular classes of LPs) exists, and these are often crucial for solving the increasingly large instances of LPs arising in industry.
Mixed Integer Programs (MIPs)
Many problems can be modeled satisfactorily as Linear Programs (LPs), i.e., with variables that are only restricted to having values in continuous intervals. However, a common class of problems requires modeling using discrete variables. These problems are called Mixed Integer Programs (MIPs). MIP problems are often hard to solve and may require large amounts of computation time to obtain even satisfactory, if not optimal, results.
Perhaps the most common use of the FICO Xpress Optimization Suite is for solving MIP problems and it is designed to handle the most challenging of these problems. Besides providing solution support for MIP problems the Optimizer provides support for a variety of popular MIP modeling constructs:
Binary variables – decision variables that have value either 0 or 1, sometimes called 0/1 variables;
Integer variables – decision variables that have integer values;
Semi-continuous variables – decision variables that either have value 0, or a continuous value above a specified non-negative limit. Semi-continuous variables are useful for modeling cases where, for example, if a quantity is to be supplied at all then it will be supplied starting from some minimum level (e.g., a power generation unit);
Semi-continuous integer variables – decision variables that either have value 0, or an integer value above a specified non-negative limit;
Partial integer variables – decision variables that have integer values below a specified limit and continuous values above the limit. Partial integer variables are useful for modeling cases where a supply of some quantity needs to be modeled as discrete for small values but we are indifferent whether it is discrete when the values are large (e.g., because, say, we do not need to distinguish between 10000 items and 10000.25 items);
Special ordered sets of type one (SOS1) — a set of decision variables ordered by a set of specified continuous values (or reference values) of which at most one can take a nonzero value. SOS1s are useful for modeling quantities that are taken from a specified discrete set of continuous values (e.g., choosing one of a set of transportation capacities);
Special ordered sets of type two (SOS2) – a set of variables ordered by a set of specified continuous values (or reference values) of which at most two can be nonzero, and if two are nonzero then they must be consecutive in their ordering. SOS2s are useful for modeling a piecewise linear quantity (e.g., unit cost as a function of volume supplied);
Indicator constraints – constraints each with a specified associated binary 'controlling' variable where we assume the constraint must be satisfied when the binary variable is at a specified binary value; otherwise the constraint does not need to be satisfied. Indicator constraints are useful for modeling cases where supplying some quantity implies that a fixed cost is incurred; otherwise if no quantity is supplied then there is no fixed cost (e.g., starting up a production facility to supply various types of goods and the total volume of goods supplied is bounded above).
Piecewise linear constraints – constraints that define a piecewise linear relationship between two variables. These are defined via a set of breakpoints with linearly interpolated values between and beyond them (with the slope before the first and after the last point continuing the slope between the first/last two points). The piecewise linear functions are allowed to be discontinuous by defining multiple points with the same value of the input variable x, in which case the output variable y is allowed to take any value between the corresponding y-values of these breakpoints, while the first of them will define the slope before and the last will define the slope after this x-value. Piecewise linear constraints are useful to model e.g. transportation costs that are constant/linear in specific intervals but may jump between the different brackets.
General constraints – specific type of MIP constraints to model min, max, and, or, and absolute value relationships between two or more variables.
All of the above MIP variable types are collectively referred to as MIP entities.
Quadratic Programs (QPs)
Quadratic Programming (QP) problems are an extension of Linear Programming (LP) problems where the objective function may include a second order polynomial. An example of this is where the user wants to minimize the statistical variance (a quadratic function) of the solution values.
The FICO Xpress Optimizer can be used directly for solving QP problems with support for quadratic objectives in the MPS and LP file formats and library routines for loading QPs and manipulating quadratic objective functions.
Quadratically Constrained Quadratic Programs (QCQPs)
Quadratically Constrained Quadratic Programs (QCQPs) are an extension of the Quadratic Programming (QP) problem where the constraints may also include second order polynomials.
A QCQP problem may be written as:
\begin{array}{lrlrlrlrlrlrlrlr} \text{minimize} & c_1 x_1 & + & \dots & + & c_n x_n & + & x^TQ_0 x\\ \text{subject to} & a_{11} x_1 & + & \dots & + & a_{1n} x_n & + & x^TQ_1 x & \leq & b_1\\ & & & \vdots\\ & a_{m1} x_1 & + & \dots & + & a_{mn} x_n & + & x^TQ_m x & \leq & b_m\\ & l_1 \leq x_1 \leq u_1, & & \dots & & l_n \leq x_n \leq u_n & & & & \end{array}where any of the lower or upper bounds \( l_{i} \) or \( u_{i} \) may be infinite.
The FICO Xpress Optimizer can be used directly for solving QCQP problems with support for quadratic constraints and quadratic objectives in the MPS and LP file formats and library routines for loading QCQPs and manipulating quadratic objective functions and the quadratic component of constraints.
Properties of QCQP problems are discussed in the following few sections.
Algebraic and matrix form
Each second order polynomial can be expressed as \( x^TQx \) where \( Q \) is an appropriate symmetric matrix: the quadratic expressions are generally either given in the algebraic form
\[ a_{11}x_1^2+2a_{12}x_1x_2+2a_{13}x_1x_3+...+a_{22}x_2^2+2a_{23}x_2x_3+... \]like in LP files, or in the matrix form \( x^TQx \) where
\[ Q = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \\ \vdots & & \ddots \\ a_{n1} & & & a_{nn} \end{pmatrix} \]like in MPS files. As symmetry is always assumed, \( a_{ij}=a_{ji} \) for all index pairs \( (i,j) \).
Convexity
A fundamental property for nonlinear optimization problems, thus in QCQP as well, is convexity. A region is called convex if for any two points from the region the connecting line segment is also part of the region.
The lack of convexity may give rise to several unfavorable model properties. Lack of convexity in the objective may introduce the phenomenon of locally optimal solutions that are not global ones (a local optimal solution is one for which a neighborhood in the feasible region exists in which that solution is the best). While the lack of convexity in constraints can also give rise to local optima, they may even introduce non-connected feasible regions as shown in Figure Non-connected feasible regions.
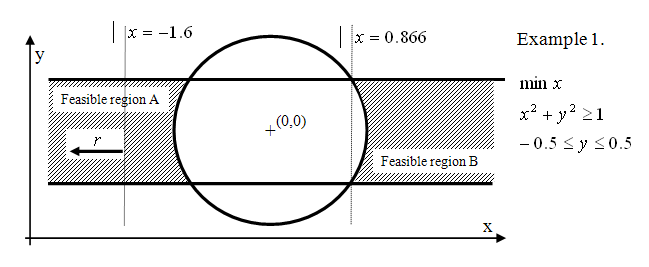
Figure 3.1: Non-connected feasible regions
In this example, the feasible region is divided into two parts. In region B, the objective function has two alternative locally optimal solutions, while in region A the objective function is not even bounded.
For convex problems, each locally optimal solution is a global one, making the characterization of the optimal solution efficient.
Characterizing Convexity in Quadratic Constraints
A quadratic constraint of the form
\[ a_1x_1+...+a_nx_n+x^TQx \leq b \]defines a convex region if and only if \( Q \) is a so-called positive semi-definite (PSD) matrix.
A square matrix \( Q \) is PSD by definition if for any vector (not restricted to the feasible set of a problem) \( x \) it holds that \( x^TQx \geq 0 \).
It follows that for greater-than or equal constraints
\[ a_1x_1+...+a_nx_n+x^TQx \geq b \]the negative of \( Q \) must be PSD.
A nontrivial quadratic equality constraint (one for which not every coefficient is zero) always defines a non-convex region (or in other words, if both \( Q \) and its negative is PSD, then \( Q \) must be equal to the 0 matrix). Therefore, quadratic equality constraints require the functionality of FICO Xpress Global, which can solve non-convex optimization problems.
Determining whether a matrix is PSD is not always obvious nor trivial. There are certain constructs, however, that can easily be recognized as being non convex:
- the product of two variables, say \( xy \), without having both \( x^2 \) and \( y^2 \) present;
- having \( - x^2 \) in any quadratic expression in a less than or equal constraint, or having \( x^2 \) in any greater than or equal constraint.
Second Order Cone problems (SOCPs)
Second order cone problems (SOCP) are a special class of quadratically constrained problems, where the quadratic matrix \( Q \) is not required to be semi-definite.
The FICO Xpress Optimizer supports (mixed integer) second order cone problems that satisfy the following requirements.
Each quadratic constraint satisfies one of the following two forms:
- Second order (or Lorentz) cone: \( x_1^2 + x_2^2 + \dots + x_k^2 - t^2 \leq 0 \) where \( t \geq 0 \)
- Rotated second order (or Lorentz) cone: \( x_1^2 + x_2^2 + \dots + x_k^2 - 2 t_1t_2 \leq 0 \) where \( t_1, t_2 \geq 0 \)
All of the cone coefficients must be exactly one, except for the coefficient of 2 for the \( t_1 t_2 \)-product. Constants or linear terms are not allowed.
For barrier solves, the cones should not overlap, i.e., any variable x may only appear in a single cone. Otherwise a transformation will be be applied that allows the problem to be solved with barrier, but it might not be possible to obtain the optimal dual values in this case.
Second order cone problems are loaded using the same API functions as for quadratic constraints, and the conic constraints are auto-detected by the optimizer at run time.
© 2001-2024 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

