Arrays, sets, lists, records, and user types
Topics covered in this chapter:
- Arrays
- Initializing sets
- Working with sets
- Initializing lists
- Working with lists
- Records
- User types
- Unions
The Mosel language defines the structured types set, array, list, and record. So far we have worked with arrays and sets relying on an intuitive understanding of what is an `array' or a `set'. More formally, we may define an array as a collection of labeled objects of a given type where the label of an array entry is defined by its index tuple.
A set collects objects of the same type without establishing an order among them (as opposed to arrays and lists). Set elements are unique: if the same element is added twice the set still only contains it once.
A list groups objects of the same type. Unlike sets, a list may contain the same element several times. The order of the list elements is specified by construction.
Mosel arrays, sets and lists may be defined for any type, that is the elementary types (including the basic types integer, real, string, boolean and the MP types mpvar and linctr), structured types (array, set, list, record), and external types (contributed to the language by a module).
A record is a finite collection of objects of any type. Each component of a record is called a field and is characterized by its name and its type.
This chapter first presents in a more systematic way the different possibilities of how arrays and sets may be initialized (all of which the reader has already encountered in the examples in the first part), and also shows more advanced ways of working with sets. We then introduce lists, showing how to initialize and access them, and finally give some examples of the use of records.
The last two sections deal with the definition of user types, including how to work with unions.
Arrays
In the first part of this manual we have already encountered many examples that make use of arrays. The most important points are summarized in this section and here is an overview of the topics explained with other examples:
- The initialization operator :: and value assignment: Section The burglar problem
- Multidimensional arrays: Section The burglar problem
- String indices: Section The burglar problem revisited
- Initialization from file:
– dense format text file (Section A blending example),
– ODBC connection (Section Reading data from spreadsheets and databases),
– Excel spreadsheets (Section Excel spreadsheets),
– sparse format text file (Section A transport example),
– alternative text formats (Section Reading sparse data) - Dynamic variable creation and finalization: Section Conditional variable creation and create
Array declaration
Here are some examples of array definition:
declarations
A1: array(1..3) of integer ! Fixed size array
F = {"a","b","c"}
A2: array(F) of real ! Fixed size array
A3: array(R:range) of integer ! Dense array with unknown index set
A4: dynamic array(F) of real ! Dynamic array
end-declarations
writeln("A1:", A1, " A2:", A2, " A3:", A3, " A4:", A4, " A5:", A5)
! Using the array initialization operator
A1::[10,20,30] ! Range indices are known
A2::(["a","b","c"])[1.1, 2.5, 3.9] ! String indices must be stated
A3::(1..3)[10,20,30] ! Indices are not known upfront
A2("a"):=5.1 ! Redefine an entry
setrandseed(3)
forall(f in F) A4(f):= 10*random ! Value assignment
delcell(A4("a")) ! Deleting an array entry
writeln("A1:", A1, " A2:", A2, " A3:", A3, " A4:", A4)
The output produced by this model (file arraydef.mos) is the following.
A1:[0,0,0] A2:[0,0,0] A3:[] A4:[] A1:[10,20,30] A2:[5.1,2.5,3.9] A3:[(1,10),(2,20),(3,30)] A4:[(`b',7.6693),(`c',5.89101)]
Arrays A1 and A2 are fixed size arrays: their size (i.e. the total number of objects/cells they contain) is known at their declaration because all their indexing sets are of fixed size (i.e. either constant or finalized). All the cells of fixed size arrays are created and initialized immediately, using default initialization values that depend on the array type. For Mosel's basic types these are the following values.
real, integer: 0
boolean: false
string: '' (i.e. the empty string)
Array A4 is explicitly marked as dynamic array using the qualifier dynamic. Dynamic arrays along with hashmap arrays are the two forms of sparse arrays in Mosel, a hashmap array is obtained by applying the qualifier hashmap in place of dynamic—both types are used in the same way, but their performance differs (dynamic arrays are generally faster for linear enumeration and require less memory whereas hashmap arrays are faster for random access). Sparse arrays are created empty. Their cells are created explicitly (see Paragraph create below) or when they are assigned a value, that is, the array size will grow `on demand'. It is also possible to delete some or all cells of a sparse array using the procedure delcell on an entry or the whole array (same as reset). The value of a cell that has not been created is the default initial value of the type of the array.
Array A3 is created empty since its indexing set is empty at the time of its declaration, but this array is not the same as a dynamic array. It is a dense array that will grow if elements are added to its index set. Please refer to Appendix Finalizing sets and dynamic arrays for further detail.
Multiple indices and array access functions
Arrays with multiple indices are defined and accessed as follows:
declarations
C: array(range, set of string, set of real) of integer
D: array(1..5) of array(range, set of string) of real
end-declarations
C(5,"ab",1.5):= 10
C(5,"dce",2.5):= 15
writeln("C=", C, ", size of C: ", C.size, ", number of dimensions: ", C.nbdim)
forall(i in 1..getnbdim(C))
writeln(" index set ", i, " = ", C.index(i), " (size:", C.index(i).size, ")")
! Alternative syntax for accessing entries of 'array of array' structures
D(1,7,"a"):= 2.8
D(1)(9,"b"):= 20
As shown in the example, in order to access (or 'dereference') the cell of an array of arrays such as the array D, the list of indices for the second array can either be appended to the list of indices of the first array, or alternatively, a second set of parantheses can be used for the index tuple of the second array.
Mosel defines various access functions for retrieving information about arrays (getsize, getnbdim, getindex) that can also be used in their dot notation form as shown in the example. The code snippet results in the following output:
C=[10,0,0,15], size of C: 4, number of dimensions: 3
index set 1 = 5..5 (size:1)
index set 2 = {`ab',`dce'} (size:2)
index set 3 = {1.5,2.5} (size:2)
The declaration of the arrays in the code snippet above employs several different types of index sets: the most common index set types probably are range sets, and sets of types integer or string. Mosel accepts any type of set as array index (including sets of structured types), however, for most pratical purposes it is recommended to employ only constant types as array indices (that is, the four basic types integer, string, boolean, real, or external types such as date/time/datetime that support the 'constant' property: see the example in Section Dates and times as constants). Note that while it is possible to use index sets of type real for Mosel arrays this is not a generally encouraged practice: due to the underlying floating point representation it is not always guaranteed that two index values that look the same are indeed identical.
create
Special care needs to be taken in the case of sparse arrays of decision variables (and indeed with any types that do not have an assignment operator). Writing x:=1 is a syntax error if x is of type mpvar. If an array of such a type is defined as dynamic or hashmap array, then the corresponding cells are not created. The entries of the array must be created explicitly by using the procedure create since they cannot be defined by assignment. Let us simply recall here the example from Section A transport example.
declarations
REGION: set of string ! Set of customer regions
PLANT: set of string ! Set of plants
TRANSCAP: dynamic array(PLANT,REGION) of real
! Capacity on each route plant->region
flow: dynamic array(PLANT,REGION) of mpvar ! Flow on each route
end-declarations
initializations from 'transprt.dat'
TRANSCAP
end-initializations
! Create the flow variables that exist
forall(p in PLANT, r in REGION | exists(TRANSCAP(p,r)) ) create(flow(p,r))
For a more detailed discussion of decision variable creation please see Section Conditional variable creation and create.
Array initialization from file
When working with arrays, we distinguish between dense and sparse data formats. Dense data format means that only the data values are represented (see also Section A blending example); in sparse format each data entry is accompanied by its index tuple. Dense format data uses less storage space but this format can only be used if all indices are defined in the model and if no ambiguity results from the omission of the indices when transferring data. In all other cases sparse data format must be used and it is particularly recommended to use this representation if only few entries of a multidimensional array are actually defined.
declarations
A: array(1..2,1..3) of real ! Can use dense format
B: array(R:range,T:range) of real ! Requires sparse format
D: dynamic array(set of string, range) of real ! Requires sparse format
S: set of string
M: dynamic array(S) of integer ! Requires sparse format
N: dynamic array(S) of string ! Requires sparse format
end-declarations
initializations from "arrayinit.dat"
A B
D as "SomeName" ! Data label different from model name
D as "SomeName2" ! Add some more data to 'D'
[M,N] as "MNData" ! 2 arrays read from the same table
end-initializations
writeln("A:", A, " B:", B, "\nD:", D, "\nM:", M, "\nN:", N)
With this contents of the data file arrayinit.dat
A: [2 4 6 8 10 12]
B: [(1 1) 2 (1 2) 4 (1 3) 6 (2 1) 8 (2 2) 10 (2 3) 12]
SomeName: [("a" 1) 2 ("a" 2) 4 ("b" 3) 6 ("c" 4) 8 ("b" 5) 10]
SomeName2: [("a" 3) 12 ("b" 2) 14 ("b" 5) 16]
MNData: [ ("A") [2 "a"] ("B") [* "b"]
("C") [6 *] ("D") [8 "c"]
("E") [10 "b"] ]
we see the following output display when executing the model arrayinit.mos shown above:
A:[2,4,6,8,10,12] B:[2,4,6,8,10,12] D:[(`a',1,2),(`a',2,4),(`a',3,12),(`b',2,14),(`b',3,6),(`b',5,16),(`c',4,8)] M:[(`A',2),(`C',6),(`D',8),(`E',10)] N:[(`A',a),(`B',b),(`D',c),(`E',b)]
By default, Mosel expects that data labels are the same as the model names. For array D we show how to read data using different labels. The contents of the second set of data labeled SomeName2 is added to what is read from SomeName. Note that the entry (b,5) is contained in both sets, and the corresponding array entry takes its value from the last label that is read.
Arrays such as M and N, that share the same index sets (but not necessarily the same entries) can be read from a single label/data table. The `*' in certain entries of MNData indicates that the entry does not exist in one of the arrays.
The syntax of initializations blocks remains the same when switching to other data sources. Sections Reading data from spreadsheets and databases and Excel spreadsheets discuss examples of using databases or spreadsheets instead of text files for array initialization. For further detail on data I/O using different data sources the reader is refered to the Xpress whitepaper Using ODBC and other database interfaces with Mosel.
Automatic arrays: the array operator
The keyword array can be used as an aggregate operator in order to create an array that will exist only for the duration of the expression. This automatic array may be used wherever a reference to an array is expected, for instance, in function calls or in initializations blocks.
In the following example we use the array operator to extract the (1-dimensional) rows and column arrays from a 2-dimensional array, we further generate a subarray with a selection of entries and the transposed (inversed indices) array.
model "Automatic arrays"
declarations
B: array(S:set of string, I:set of real) of integer
end-declarations
B::(["a","b"], [3,1.5,7])[1,2,3,4,5,6]
writeln("B: ", B)
forall(s in S) writeln("Row ", s, ": ", array(i in I) B(s,i))
forall(i in I) writeln("Column ", i, ": ", array(s in S) B(s,i))
writeln("B filtered: ", array(s in S,i in I | s<>"a" and i<5) B(s,i))
writeln("Transpose: ", array(i in I, s in S) B(s,i))
end-model
And this is the output generated by the model autoarray.mos.
B: [1,2,3,4,5,6] Row a: [1,2,3] Row b: [4,5,6] Column 3: [1,4] Column 1.5: [2,5] Column 7: [3,6] B filtered: [(`b',3,4),(`b',1.5,5)] Transpose: [1,4,2,5,3,6]
As it has been mentioned in Section Multiple indices and array access functions the use index sets of type real for Mosel arrays is not a generally encouraged practice: due to the underlying floating point representation it is not always guaranteed that two index values that look the same are indeed identical.
On the topic of output to file using initializations to, see Chapter Output, and particularly the note on solution output using arrays generated 'on the fly' in combination with evaluation of in Section Solution output with initializations to.
Initializing sets
In the revised formulation of the burglar problem in Chapter Some illustrative examples and also in the models in Chapter More advanced modeling features we have already seen different examples for the use of index sets. We recall here the relevant parts of the respective models.
Constant sets
In the Burglar example the index set is assigned directly in the model:
declarations
ITEMS={"camera", "necklace", "vase", "picture", "tv", "video",
"chest", "brick"}
end-declarations
Since in this example the set contents is set in the declarations section, the index set ITEMS is a constant set (its contents cannot be changed). To declare it as a dynamic set, the contents needs to be assigned after its declaration:
declarations
ITEMS: set of string
end-declarations
ITEMS:={"camera", "necklace", "vase", "picture", "tv", "video",
"chest", "brick"}
Set initialization from file, finalized and fixed sets
In Chapter Integer Programming the reader has encountered several examples how the contents of sets may be initialized from data files.
The contents of the set may be read in directly as in the following case:
declarations WHICH: set of integer end-declarations initializations from 'idata.dat' WHICH end-initializations
Where idata.dat contains data in the following format:
WHICH: [1 4 7 11 14]
Unless a set is constant (or finalized), arrays that are indexed by this set (and that are not explicitly marked as sparse arrays) are created as non-fixed dense arrays. Since in many cases the contents of a set does not change any more after its initialization, Mosel's automatic finalization mechanism finalizes the set WHICH in the initializations from block. Consider the continuation of the example above:
declarations x: array(WHICH) of mpvar end-declarations
The array of variables x will be created as a static array since its index set is finalized. Declaring arrays in the form of static arrays is preferable if the indexing set is known before because this allows Mosel to handle them in a more efficient way.
Index sets may also be initialized indirectly during the initialization of non-fixed or sparse arrays:
declarations REGION: set of string DEMAND: array(REGION) of real end-declarations initializations from 'transprt.dat' DEMAND end-initilizations
If file transprt.dat contains the data:
DEMAND: [(Scotland) 2840 (North) 2800 (West) 2600 (SEast) 2820 (Midlands) 2750]
then printing the set REGION after the initialization will give the following output:
{`Scotland',`North',`West',`SEast',`Midlands'}
Once a set is used for indexing an array (of data, decision variables etc.) it is fixed, that is, its elements can no longer be removed, but it may still grow in size.
The indirect initialization of (index) sets is not restricted to the case that data is input from file. In the following example (model chess2.mos) we add an array of variable descriptions to the chess problem introduced in Chapter Getting started with Mosel. These descriptions may, for instance, be used for generating a nice output. Since the indexing set Allvars of array DescrV is not known at declaration time the resulting array is not fixed and both grow with each new variable description that is added to DescrV.
model "Chess 2"
uses "mmxprs"
declarations
Allvars: set of mpvar
DescrV: array(Allvars) of string
small, large: mpvar
end-declarations
DescrV(small):= "Number of small chess sets"
DescrV(large):= "Number of large chess sets"
Profit:= 5*small + 20*large
Lathe:= 3*small + 2*large <= 160
Boxwood:= small + 3*large <= 200
maximize(Profit)
writeln("Solution:\n Objective: ", getobjval)
writeln(DescrV(small), ": ", getsol(small))
writeln(DescrV(large), ": ", getsol(large))
end-model
The reader may have already remarked another feature that is illustrated by this example: the indexing set Allvars is of type mpvar. So far only basic types have occurred as index set types but as mentioned earlier, sets in Mosel may be of any elementary type, including the MP types mpvar and linctr.
Working with sets
In all examples of sets given so far sets are used for indexing other modeling objects. But they may also be used for different purposes.
The following example (model setops.mos) demonstrates the use of basic set operations in Mosel: union (+), intersection (*), and difference (-):
model "Set example"
declarations
Cities={"rome", "bristol", "london", "paris", "liverpool"}
Ports={"plymouth", "bristol", "glasgow", "london", "calais",
"liverpool"}
Capitals={"rome", "london", "paris", "madrid", "berlin"}
end-declarations
Places:= Cities+Ports+Capitals ! Create the union of all 3 sets
In_all_three:= Cities*Ports*Capitals ! Create the intersection of all 3 sets
Cities_not_cap:= Cities-Capitals ! Create the set of all cities that are
! not capitals
writeln("Union of all places: ", Places)
writeln("Intersection of all three: ", In_all_three)
writeln("Cities that are not capitals: ", Cities_not_cap)
end-model
The output of this example will look as follows:
Union of all places:{`rome',`bristol',`london',`paris',`liverpool',
`plymouth',`bristol',`glasgow',`calais',`liverpool',`rome',`paris',
`madrid',`berlin'}
Intersection of all three: {`london'}
Cities that are not capitals: {`bristol',`liverpool}
Sets in Mosel are indeed a powerful facility for programming as in the following example (model prime.mos) that calculates all prime numbers between 2 and some given limit.
Starting with the smallest one, the algorithm takes every element of a set of numbers SNumbers (positive numbers between 2 and some upper limit that may be specified when running the model), adds it to the set of prime numbers SPrime and removes the number and all its multiples from the set SNumbers.
model Prime
parameters
LIMIT=100 ! Search for prime numbers in 2..LIMIT
end-parameters
declarations
SNumbers: set of integer ! Set of numbers to be checked
SPrime: set of integer ! Set of prime numbers
end-declarations
SNumbers:={2..LIMIT}
writeln("Prime numbers between 2 and ", LIMIT, ":")
n:=2
repeat
while (not(n in SNumbers)) n+=1
SPrime += {n} ! n is a prime number
i:=n
while (i<=LIMIT) do ! Remove n and all its multiples
SNumbers-= {i}
i+=n
end-do
until SNumbers={}
writeln(SPrime)
writeln(" (", getsize(SPrime), " prime numbers.)")
end-model
This example uses a new function, getsize, that if applied to a set returns the number of elements of the set. The condition in the while loop is the logical negation of an expression, marked with not: the loop is repeated as long as the condition n in SNumbers is not satisfied.
Set operators
The preceding example introduces the operator += to add sets to a set (there is also an operator -= to remove subsets from a set). Another set operator used in the example is in denoting that a single object is contained in a set. We have already encountered this operator in the enumeration of indices for the forall loop.
Mosel also defines the standard operators for comparing sets: subset (<=), superset (>=), difference (<>), end equality (=). Their use is illustrated by the following example (model setcomp.mos):
model "Set comparisons"
declarations
RAINBOW = {"red", "orange", "yellow", "green", "blue", "purple"}
BRIGHT = {"yellow", "orange"}
DARK = {"blue", "brown", "black"}
end-declarations
writeln("BRIGHT is included in RAINBOW: ", BRIGHT <= RAINBOW)
writeln("RAINBOW is a superset of DARK: ", RAINBOW >= DARK)
writeln("BRIGHT is different from DARK: ", BRIGHT <> DARK)
writeln("BRIGHT is the same as RAINBOW: ", BRIGHT = RAINBOW)
end-model
As one might have expected, this example produces the following output:
BRIGHT is included in RAINBOW: true RAINBOW is a superset of DARK: false BRIGHT is different from DARK: true BRIGHT is the same as RAINBOW: false
Initializing lists
Lists are not commonly used in the standard formulation of Mathematical Programming problems. However, this data structure may be useful for the Mosel implementation of some more advanced solving and programming tasks.
Constant list
If the contents of a list are specified at the declaration of the list, such as
declarations L = [1,2,3,4,5,6,7,8,9,10] end-declarations
we have defined a constant list (its contents cannot be changed). If we want to be able to modify the list contents subsequently we need to separate the definition of the list contents from the declaration, resulting in a dynamic list:
declarations L: list of integer end-declarations L:= [1,2,3,4,5,6,7,8,9,10]
A two-dimensional array of lists may be defined thus (and higher dimensional arrays by analogy):
declarations M: array(range,set of integer) of list of string end-declarations M:: (2..4,1)[['A','B','C'], ['D','E'], ['F','G','H','I']]
List initialization from file
Similarly to what we have already seen for other data structures, the contents of lists may be initialized from file through initializations blocks. For example,
declarations
K: list of integer
N: array(range,set of integer) of list of string
end-declarations
initializations from "listinit.dat"
K N
end-initializations
writeln("K: ", K)
writeln("An entry of N: ", N(5,3))
Assuming the datafile listinit.dat contains these lines
K: [5 4 3 2 1 1 2 3 4 5]
N: [(3 1) ['B' 'C' 'A']
(5 3) ['D' 'E']
(6 1) ['H' 'I' 'F' 'G']]
we obtain the following output from the model fragment above:
K: [5,4,3,2,1,1,2,3,4,5] An entry of N: [`D',`E']
Working with lists
Enumeration
Similarly to the way we have used sets so far, lists may be used as loop indices for enumeration. The following enumerates a given list L from beginning to end:
declarations L: list of integer end-declarations L:= [1,2,3,4,5] forall(i in L) writeln(i)
Since lists have an ordering we may choose, for instance, to reverse the order of list elements for the enumeration. The model listenum.mos below shows several possibilities for enumerating lists in inverse order: (1) reversing a copy of the list to enumerate, (2) reversing the list to enumerate. In the first case we obtain the reversed copy of the list with function getreverse, in the second case we modify the original list by applying to it the procedure reverse.
model "Reversing lists" declarations K,L: list of integer end-declarations L:= [1,2,3,4,5] ! Enumeration in inverse order: ! 1. Reversed copy of the list (i.e., no change to 'L') K:=getreverse(L) forall(i in K) writeln(i) ! 2. Reversing the list itself reverse(L) forall(i in L) writeln(i) end-model
List operators
Lists are composed by concatenating several lists or by truncating their extremities (refered to as head and tail). The operators += and + serve for concatenating lists. Their inverses (-= and -) may be used to remove the tail of a list—they will not remove the given sublist if it is not positioned at the end.
The following model listops.mos shows some examples of the use of list operators. Besides the concatenation operators + and += we also use the aggregate form sum. Another list operator used in this example is the comparison operator <> (the comparison operator = may also be used with lists).
model "List operators"
declarations
L,M: list of integer
end-declarations
L:= [1,2,3] + [4,5]; writeln("L (1): ", L)
L+= [6,7,8]; writeln("L (2): ", L)
L-= [1,2,3]; writeln("L (3): ", L)
M:= sum(l in L) [l*2]; writeln("M: ", M)
writeln("L and M are different: ", L<>M)
end-model
As can be seen in the output, the list [1,2,3] is not removed from L since it is not located at its tail:
L (1): [1,2,3,4,5] L (2): [1,2,3,4,5,6,7,8] L (3): [1,2,3,4,5,6,7,8] M: [2,4,6,8,10,12,14,16] L and M are different: true
List handling functions
The Mosel subroutines for list handling form two groups, namely
- Operations preserving the list they are applied to: retrieving a list element (getelt, getfirst, getlast), occurrence of an element (findfirst, findlast), retrieving a copy of the head or tail (gethead, gettail), reversed copy of a list (getreverse)
- Operations modifying the list they are applied to: cutting off (=discard) individual elements or the head or tail (cutelt, cutfirst, cutlast, cuthead, cuttail), splitting off (=retrieve) the head or tail (splithead, splittail), reverse the list (reverse)
The following example listmerge.mos merges two lists of integers K and L, the elements of which are ordered in increasing order of their values into a new list M that is ordered in the same way. The elements of the two original lists are added one-by-one to the new list using the concatenation operator +=. Whilst the elements of the list K are simply enumerated, we iteratively split off the first element from list L (using splithead with second argument 1 to take away just the first list element) so that this list will be empty at the end of the forall loop. If this is not desired, we need to work with a copy of this list.
model "Merging lists" declarations K,L,M: list of integer end-declarations K:= [1,4,5,8,9,10,13] L:= [-1,0,4,6,7,8,9,9,11,11] forall(k in K) do while (L<>[] and k >= getfirst(L)) M += splithead(L,1) M+= [k] end-do writeln(M) end-model
The resulting list M is:
[-1,0,1,4,4,5,6,7,8,8,9,9,9,10,11,11,13]
List handling routines provide a powerful means of programming, illustrated by the following example euler.mos that constructs a Eulerian circuit for the network shown in Figure Network forming a Eulerian circuit (thick arrows indicate that the corresponding arc is to be used twice). This example is an alternative implementation of the Eulerian circuit algorithm described in Section 15.4 `Gritting roads' (problem j4grit) of the book 'Applications of optimization with Xpress-MP'.
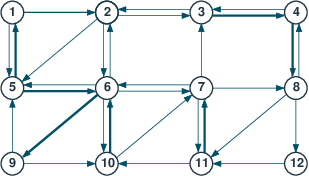
Figure 10.1: Network forming a Eulerian circuit
A Eulerian circuit is a tour through a network that uses every given arc exactly once. To construct such a circuit for a given set of arcs we may employ the following algorithm
- Choose a start node and add it to the tour.
- while there are unused arcs:
– Find the first node in the tour with unused outgoing arcs.
– Construct a closed subtour starting from this node.
– Insert the new subtour into the main tour.
model "Eulerian circuit"
declarations
NODES = 1..12 ! Set of nodes
UNUSED: array(NODES) of list of integer
TOUR: list of integer
NEWT, TAIL: list of integer
end-declarations
initializations from 'euler.dat'
UNUSED
end-initializations
ct:=sum(i in NODES) getsize(UNUSED(i))
TOUR:=[1] ! Choose node 1 as start point
while(ct>0) do ! While there are unused arcs:
! Find first node in TOUR with unused outgoing arc(s)
node:=0
forall(i in TOUR)
if UNUSED(i) <> [] then
node:=i
break
end-if
! Insertion position (first occurrence of 'node' in TOUR)
pos:= findfirst(TOUR, node)
! Construct a new subtour starting from 'node'
cur:=node ! Start with current node
NEWT:=[]
while(UNUSED(cur) <> []) do
NEWT+=splithead(UNUSED(cur),1) ! Take first unused arc
cur:=getlast(NEWT) ! End point of arc is new current node
end-do
! Stop if the subtour is not a closed loop (=> no Eulerian circuit)
if cur<>node then ! Compare start and end of subtour
writeln("Tour cannot be closed")
exit(1)
end-if
! Add the new subtour to the main journey
TAIL:=splittail(TOUR, -pos) ! Split off the tail from main tour
TOUR += NEWT + TAIL ! Attach subtour and tail to main tour
ct -= getsize(NEWT)
end-do
writeln("Tour: ", TOUR) ! Print the result
end-model
The data file euler.dat corresponding to the graph in Figure Network forming a Eulerian circuit has the following contents:
UNUSED: [(1) [2 5] (2) [3 5 6] (3) [2 4 4] (4) [3 8 8]
(5) [1 1 6 6] (6) [2 5 7 9 9 10] (7) [3 6 8 11]
(8) [4 11 12] (9) [5 10] (10) [6 6 7]
(11) [7 7 10] (12) [11] ]
A Eulerian circuit for this data set is the tour
1 → 2 → 6 → 5 → 6 → 7 → 8 → 12 → 11 → 7 → 11 → 10 → 7 → 3 → 4 → 3 → 4 → 8 → 4 → 8 → 11 → 7 → 6 → 9 → 5 → 6 → 9 → 10 → 6 → 10 → 6 → 2 → 3 → 2 → 5 → 1 → 5 → 1
Records
Records group Mosel objects of different types. They may be used, for instance, to structure the data of a large-scale model by collecting all information relating to the same object.
Defining records
The definition of a record has some similarities with the declarations block: it starts with the keyword record, followed by a list of field names and types, and the keyword end-record marks the end of the definition. The definition of records must be placed in a declarations block. The following code extract defines a record with two fields (`name' and `values').
declarations R = 1..10 D: record name: string values: array(R) of real end-record end-declarations
We need to define a name (e.g., `mydata') for the record if we want to be able to refer to it elsewhere in the model—note that we declare this record as public in order to make all its fields public (so in particular, visible in output display), alternatively, individual fields can be declared as public. For example:
declarations
R = 1..10
mydata = public record
name: string
values: array(R) of real
end-record
D: mydata
A: array(range) of mydata
end-declarations
The fields of a record are accessed by appending .fieldname to the record, for instance:
D.name:= "D"
forall(i in R) D.values(i):= i
writeln("Values of ", D.name, ": ", D.values)
writeln("An entry of A: ", A(1))
writeln("'name' of an entry of A: ", A(4).name)
writeln("'values' of an entry of A: ", A(3).values)
writeln("First entry of 'values': ", A(3).values(1))
Note: if a record field is an array, the index set(s) of the array can be either constant, or be declared outside of the record definition, or remain unnamed. So, these are all valid record definitions:
declarations
R: range
P: record
values: array(R) of real
end-record
Q: record
values: array(1..10) of real
end-record
T = record
values: array(range) of real
end-record
L: list of T
end-declarations
Working with unnamed index sets for a record field means that each entry of the list L has its own index set the contents of which is not influenced by any of the other list entries—if a set name was specified for the array values in the record type definition for T all entries of L would be sharing the same index set.
Initialization of records from file
The contents of a record may be assigned fieldwise within a model as shown above or else be read in from file using initializations. The data file must contain the data entries for the different record fields in their order of occurrence in the record definition. An array A of the record type mydata defined in the previous section is initialized with data from file in the obvious way (model recorddef.mos):
declarations A: dynamic array(T:range) of mydata end-declarations initializations from "recorddef.dat" A end-initializations writeln(A(1)) forall(i in T | exists(A(i))) writeln(A(i).name)
If the data file recorddef.dat has these contents:
A: [(1) ['A1' [(2) 2 (3) 3 (4) 4] ]
(3) ['A3' [(3) 6 (6) 9] ]
(4) ['A4' [5 6 7 8] ]
(7) ['A7'] ! Define just the first field
(6) [* [(6) 6] ] ! Skip the first field
]
we obtain the following output (the entry with index 6 is defined but has no name, which accounts for the empty line between 'A4' and 'A7'):
[name=`A1' values=[0,2,3,4,0,0,0,0,0,0]] A1 A3 A4 A7
An example of the use of records is the encoding of arcs and associated information such as for representing the network in Figure Network with costs on arcs.
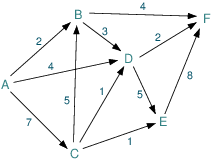
Figure 10.2: Network with costs on arcs
A data file with the network data may look as follows (file arcs.dat):
ARC: [(1) ["A" "B" 2]
(2) ["A" "D" 4]
(3) ["A" "C" 7]
(4) ["B" "F" 4]
(5) ["B" "D" 3]
(6) ["C" "B" 5]
(7) ["C" "D" 1]
(8) ["C" "E" 1]
(9) ["D" "F" 2]
(10) ["D" "E" 5]
(11) ["E" "F" 8] ]
We may then write our model arcs.mos thus
model "Arcs"
declarations
NODES: set of string ! Set of nodes
ARC: array(ARCSET:range) of record ! Arcs:
Source,Sink: string ! Source and sink of arc
Cost: real ! Cost coefficient
end-record
end-declarations
initializations from 'arcs.dat'
ARC
end-initializations
! Calculate the set of nodes
NODES:=union(a in ARCSET) {ARC(a).Source, ARC(a).Sink}
writeln(NODES)
writeln("Average arc cost: ", sum(a in ARCSET) ARC(a).Cost / getsize(ARCSET) )
end-model
The record definition may contain additional fields (e.g., decision variables) that are not to be initialized from file. In this case we need to specify in the initializations block which record fields are to be filled with data (example arcs2.mos).
declarations
NODES: set of string ! Set of nodes
ARC: array(ARCSET:range) of record ! Arcs:
flow: mpvar ! Flow quantity
Source,Sink: string ! Source and sink of arc
Cost: real ! Cost coefficient
end-record
end-declarations
initializations from 'arcs.dat'
ARC(Source,Sink,Cost)
end-initializations
This functionality can also be used to read separately, and possibly from different sources, the contents of the record fields (example arcs3.mos). For instance, the 'Cost' field of our record ARC could be initialized as follows:
initializations from 'arcs.dat' ARC(Cost) as "COST" end-initializations
where the data array 'COST' is given as
COST: [(1) 2 (2) 4 (3) 7 (4) 4 (5) 3 (6) 5
(7) 1 (8) 1 (9) 2 (10) 5 (11) 8]
User types
In a Mosel model, the user may define new types that will be treated in the same way as the predefined types of the Mosel language. New types are defined in declarations blocks by specifying a type name, followed by =, and the definition of the type. The simplest form of a type definition is to introduce a new name for an existing type, such as:
declarations myint = integer myreal = real end-declarations
In the section on records above we have already seen an example of a user type definition for records (where we have named the record `mydata'). Another possible use of a user type is as a kind of `shorthand' where several (data) arrays have the same structure, such as in the model blend.mos from Chapter Some illustrative examples, where, instead of
declarations ORES = 1..2 ! Range of ores COST: array(ORES) of real ! Unit cost of ores AVAIL: array(ORES) of real ! Availability of ores GRADE: array(ORES) of real ! Grade of ores (measured per unit of mass) end-declarations
we could have written
declarations ORES = 1..2 ! Range of ores myarray = array(ORES) of real ! Define a user type COST: myarray ! Unit cost of ores AVAIL: myarray ! Availability of ores GRADE: myarray ! Grade of ores (measured per unit of mass) end-declarations
without making any other modifications to the model.
Type constructors
The following example (file arcs4.mos) defines the 'arc' record structure that we have seen in the previous section as a user type and employs this type in the definition of another data structure.
public declarations
NODES: list of string ! List of nodes
arc = public record ! Arcs:
Source,Sink: string ! Source and sink of arc
Cost: real ! Cost coefficient
end-record
ARCLIST: list of arc
end-declarations
NODES:=['A','B','C','D','E','F']
i:='S'; ct:=0
forall(j in NODES, ct as counter) do
ARCLIST+= [arc(.Source:=i,.Sink:=j,.Cost:=10*ct)]
i:=j
end-do
writeln(ARCLIST)
In this example, the type name 'arc' is used as type constructor for populating the list ARCLIST with 6 different entries, namely:
[[Source=`S' Sink=`A' Cost=10],[Source=`A' Sink=`B' Cost=20], [Source=`B' Sink=`C' Cost=30],[Source=`C' Sink=`D' Cost=40], [Source=`D' Sink=`E' Cost=50],[Source=`E' Sink=`F' Cost=60]]
Type constructors for records can be used to populate all or only a selection of the record fields. For example, this code snippet
! Initializing selected record fields writeln(arc(.Source:="S")) writeln(arc(.Sink:="Z")) writeln(arc(.Cost:=100,.Source:="XYZ"))
will result in the following output:
[Source=`S' Sink=`' Cost=0] [Source=`' Sink=`Z' Cost=0] [Source=`XYZ' Sink=`' Cost=100]
Further examples of type constructors are discussed in Section Date and time data types for the creation of date, time, and datetime data.
Unions
A union is a container capable of holding an object of one of a predefined set of types. One possible use of this functionality is for reading and storing input data of a-priori unknown type. It can also be helpful for advanced programming tasks involving retrieval of information from another Mosel model without prior knowledge of its structure/data model or for inspecting and modifying in a generic way the running model itself (the latter is typically refered to as reflection, see the Mosel Language Reference Manual chapter on mmreflect for further detail).
Defining unions
Defining an entity of a union type consists in specifying the set of compatible types or the predefined union type any than can handle any type without restriction.
declarations u: string or real ! Scalar accepting 'string' or 'real' a: any ! Entity accepting any type ! Defining a type name for the union of the 4 basic Mosel types: basictype = string or integer or real or boolean B: array(range) of basictype ! Array of union type 'basictype' end-declarations
The first type that is specified for a union has a special meaning as it defines the representation to use when the union is initialized from some textual form, besides that, order has no impact. In the case of the predefined union type any the textual representation is handled by a string. If any of the specified compatible types is itself a union the resulting set of compatible types will include all types of this union.
The type of a union is determined when a value is assigned to the entity, it can be retrieved via gettypeid or using the operator is:
declarations
u: string or real ! Scalar accepting 'string' or 'real'
end-declarations
u:="a"
writeln(u, " is string: ", u.typeid = string.id) ! Output: true
u:=7.5
writeln(u, " is real: ", u.typeid = real.id) ! Output: true
! The preceding line is equivalent to:
writeln(u, " is real: ", u is real) ! Output: true
It is possible to force a particular type in assignments. You need to employ the create procedure for types that do not support assignment such as 'mpvar':
declarations
a: any ! Entity accepting any type
end-declarations
a.real:=10
writeln(a, ":", a is real, a is integer) ! Output: true false
a.text:="a text"
writeln(a, ":", a is text, a is string) ! Output: true false
create(a.mpvar)
writeln(getsol(a.mpvar), ":", a is mpvar) ! Output: true
A union entity can be assigned a compatible union type, but if its type is not compatible with the destination of the assignment a runtime error will be raised. A wrapping mechanism is used when a subroutine expects a union but it receives a compatible type or a different union type:
declarations
u: string or real ! Scalar accepting 'string' or 'real'
a: any ! Entity accepting any type
! Defining a type name for the union of the 4 basic Mosel types:
basictype = string or integer or real or boolean
B: array(range) of basictype ! Array of union type 'basictype'
end-declarations
! This subroutine accepts any union type as its argument
procedure dosomething(aunion: any)
writeln("In procedure 1: ", aunion)
end-procedure
a:=date(2020,12,24); u:=7.5
dosomething(a)
dosomething(u)
! This subroutine only accepts compatible union types
procedure dosomething2(aunion: basictype)
writeln("In procedure 2: ", aunion)
end-procedure
a:=2; u:=7.5; B(1):="abc"
dosomething2(a) ! Type of 'a' now is integer, so it is compatible, but
! this would fail with the previous type 'date' of 'a'
dosomething2(u) ! Types of 'u' are a subset of union 'basicvalue'
dosomething2(B(1))
All our previous examples have shown how to work with scalar types in unions. But the concept of unions and the definition of any in particular is not restricted to these: the following code snippet shows how to retrieve information about collection structures (array, set or list) for entities of a union type. With collection structures the is operator can be used to check the structure, optionally in combination with the element type. Equivalenty, this information can be accessed via getstruct and geteltype. The specific access routines for a structure, such as getnbdim or getindex for arrays, can also be applied.
declarations
L: list of any ! List of type 'any'
a: any ! Entity of type 'any'
artype = dynamic array(range,string) of real ! Array type definition
rectype = public record ! Record type definition
val: real
end-record
end-declarations
!**** List and set structures
L:=[1.5, "abc", {true,false}, [1,2,3]]
writeln("L=", L)
writeln(L(1), " is real:", L(1) is real) ! Output: true
writeln(L(3), ": is set:", L(3) is set, ! Output: true
" is set of boolean:", L(3) is set of boolean, ! Output: true
" elem. type is boolean:", L(3).eltype = boolean.id) ! Output: true
writeln(L(4), ": is list:", L(4).struct=STRUCT_LIST, ! Output: true
" is list of integer:", L(4) is list of integer, ! Output: true
" elem. type is integer:", L(4).eltype = integer.id) ! Output: true
!**** Defining and accessing arrays
! Optional: explicit type specification (req. if type not used in assignment)
! create(a.artype); a.array(1,"a").real:= 1.5
a.artype(1,"b"):= 1.5; a.artype(3,"b"):= -0.5
a.array(1,"cde").real:= 7.25; ! Type has been set by prev. assignments
writeln(a, " is array:", a is array,
" is array of real:", a is array of real) ! Output: true true
writeln(" is of artype:", a is artype,
" elem. type is real:", a.eltype = real.id) ! Output: true true
writeln(" dimensions:", a.array.nbdim, " size:", a.array.size)
! Output: dimensions:2 size:3
forall(i in 1..a.array.nbdim)
writeln(" index", i, "=", a.array.index(i)) ! Output: index1=1..3
! index2={'b','cde'}
with A(I,J)=a.artype do
forall(i in I,j in J | exists(A(i,j))) writeln("A(",i,",",j,")=",A(i,j))
end-do
And similarly, a union can be of a record type.
declarations
a: any ! Entity of type 'any'
rectype = public record ! Record type definition
val: real
end-record
end-declarations
a.rectype.val:=1.25
writeln(a, " is record:", a is record, " is rectype:", a is rectype)
! Output: true true
Initialization of unions from file
When initializing unions from text format data files only scalar values of basic types are considered. More precisely, integers, reals, and Booleans are assigned to the union; textual values are used to initialize the entity as if it was of the first compatible type of the union (for the union any this is a string). An I/O error will be raised if this type does not support initialization.
declarations
L: list of any ! List of type 'any'
mytype = text or integer or real or boolean
B: array(R:range) of mytype ! Array of union type 'mytype'
TNAME: array(integer) of text ! Type names for display
end-declarations
initializations from "uniondata.dat"
L B
end-initializations
TNAME(integer.id):="integer"; TNAME(real.id):="real"
TNAME(string.id):="string"; TNAME(text.id):="text"
TNAME(boolean.id):="boolean"
writeln("L=", L)
forall(i in L) writeln(" ", i, ":", i.typeid, " ", TNAME(i.typeid))
writeln("B=", B)
forall(i in R)
writeln(" B", i, "=", B(i),":", B(i).typeid, " ", TNAME(B(i).typeid))
Assuming the data file 'uniondata.dat' has this contents:
L: [10 "abc" true 7.5] B: [(1) "abc" (3) 5 (4) 5.6 ]
then the code snippet above will produce the following output:
L=[10,abc,true,7.5] 10:1 integer abc:3 string true:4 boolean 7.5:2 real B=[abc,?,5,5.6] B1=abc:11 text B2=?:-1 B3=5:1 integer B4=5.6:2 real
When exporting unions, any non-scalar value or types that do not support conversion to string will result in a NIL value ('?' in text format files) in the generated file. Appending the following lines to the previous example
declarations x: mpvar end-declarations L+= [any(x)] initializations to "unionout.dat" L B end-initializations
will result in an output file 'unionout.dat' with this contents:
L: [10 abc true 7.5 ?] B: [(1) abc ? 5 5.6]
Working with the 'reference to' operator
The 'reference to' operator (in symbols: ->) can be defined on any globally declared entities of basic type or reference type, it can be thought of as an alias to the referenced entity.
declarations
A: array(range) of integer
end-declarations
A::(2..5)[2,4,6,8]
u:=A ! u holds a copy of A
writeln("A=", A, " u=", u) ! A=[2,4,6,8] u=[2,4,6,8]
writeln("u is array:", u is array) ! Output: true
u.array(2).integer:=10 ! Modify 'u'
writeln("A=", A, " u=", u) ! A=[2,4,6,8] u=[10,4,6,8] ('A' unchanged)
A(5):=10 ! Modify 'A'
writeln("A=", A, " u=", u) ! A=[2,4,6,10] u=[10,4,6,8] ('u' unchanged)
u:=->A ! u is a reference to A
writeln("A=", A, " u=", u) ! A=[2,4,6,10] u=[2,4,6,10]
writeln("u is array:", u is array) ! Output: true
u.array(2).integer:=-1 ! Modify 'u'
writeln("A=", A, " u=", u) ! A=[-1,4,6,10] u=[-1,4,6,10]
A(5):=25 ! Modify 'A'
writeln("A=", A, " u=", u) ! A=[-1,4,6,25] u=[-1,4,6,25]
! Reset (=delete) the reference , original array A remains unchanged
reset(u)
writeln("u is defined:", isdefined(u), " is array:", u is array) ! Output: false false
A special case (and probably the most likely use) are references to subroutines that are discussed in a separate section: see section Subroutine references below.
© 2001-2025 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

