Robust network design
Topics covered in this section:
Problem description
Suppose we want to design a Telecommunication network. We are given a set of routers, a set of links, and a set of traffic demands (measured in MB/s) between pairs of routers; for convenience we can assume each of them sits in a city. We want to find the capacity to be installed on each link in order to satisfy all traffic demands. There are several variants of this problem in the scientific literature, and an important subclass deals with the problem of provisioning virtual private networks, or VPNs for short.
In general, in VPN traffic demand is difficult to predict even in the short term, and hence the traffic demands are uncertain; however, there exist uncertainty models for such traffic demands. Here we consider one that has attracted considerable attention and that is realistic enough in VPNs. We suppose that there are two parameters si+ and si- which estimate the maximum total outgoing and incoming traffic, respectively, at node i. The problem is hence that of finding the value of the capacity of every arc of the network (which is a multiple of a given unit capacity C) so as to accommodate any traffic demand dhk from node h to node k, subject to uncertainty on these demands modeled by the upper bounds on the incoming and outgoing traffic for each node of the network.
Mathematical formulation
Consider a directed graph G with n nodes and m arcs, defined as G=(V,A), where V={1,...,n} denotes the set of n nodes and A={(i1,j1),(i2,j2),...,(im,jm)} is the set of arcs. The cost of every unit of capacity (MB/s) installed at each arc (i,j) ∈ A is denoted by aij, and, for each pair of nodes (h,k) the (unknown) traffic demand from h to k is given by dhk. Let us introduce a binary flow variable fijhk: this variable is one if demand (h,k) is routed through arc (i,j), zero otherwise, and serves to model the flow of data between each source/destination pair. We also need to introduce the integer variable xij, which represents the number of channels of capacity C to be installed in the network. This problem is a particular case of a multi-commodity network flow problems, with the important addition of the uncertain in the traffic demands.
Let us first model the uncertainty set: every uncertain demand dhk is nonnegative and the total demand leaving or entering a node i is bounded from above by a given parameter:
Let us consider now the two main classes of constraints for the problem: conservation of flow for the variables f and the capacity constraints. The former reads as follows: for each node i and each demand (h,k), if i is an intermediate node for this demand, i.e., it is neither h nor k, then the incoming flow must be equal to the outgoing flow, therefore
Implementation
Below is the implementation in Mosel: note that the option ROBUST_OVERLAP_UNCERTAIN is used since the capacity constraints at each arc use a subset of the uncertain demands.
model "Robust Network"
uses "mmrobust", "mmxprs"
parameters
vpn_data="vpn_data.dat"
end-parameters
declarations
NODES: range ! Set of nodes
ARCCOST: dynamic array(NODES, NODES) of real ! Per-unit cost of arc (i,j)
DEM_IN: array(NODES) of real ! Total INCOMING demand at each node
DEM_OUT: array(NODES) of real ! Total OUTGOING demand at each node
UNITCAP: integer ! Per-unit capacity (independent of arc)
! Decision variables
flow: dynamic array(NODES, NODES, NODES, NODES) of mpvar
! flow(i,j,h,k) is 1 iff demand h->k uses arc (i,j)
capacity: dynamic array(NODES, NODES) of mpvar ! Capacity to install on arc (i,j)
! Uncertain parameters
demand: array(NODES, NODES) of uncertain ! Uncertain traffic demand
RobustCap: array(NODES, NODES) of robustctr ! Uncertain traffic demand, formulated at each arc
end-declarations
! The following option is necessary to allow uncertain demands to be
! used across multiple capacity constraints
setparam("robust_uncertain_overlap", true)
! Set verbosity level
setparam("xprs_verbose", true)
!**** Data input ****
initializations from vpn_data
NODES ARCCOST
DEM_IN DEM_OUT
UNITCAP
end-initializations
!**** Model formulation ****
forall(i in NODES, j in NODES, h in NODES, k in NODES |
exists(ARCCOST(i,j)) and ARCCOST(i,j) > 0 and h <> k) do
create(flow(i,j,h,k))
flow(i,j,h,k) is_binary
end-do
forall(i in NODES, j in NODES | exists(ARCCOST(i,j)) and ARCCOST(i,j) > 0) do
create(capacity(i,j))
capacity(i,j) is_integer
end-do
! Flow balance at intermediate nodes for each demand(h,k)
forall(i in NODES, h in NODES, k in NODES | i <> h and i <> k and k <> h)
sum(j in NODES | exists(flow(i,j,h,k))) flow(i,j,h,k) -
sum(j in NODES | exists(flow(j,i,h,k))) flow(j,i,h,k) = 0
! Flow balance at source nodes (unnecessary for sink nodes)
forall(i in NODES, h=i, k in NODES | k <> h)
sum(j in NODES | exists(flow(i,j,h,k)) ) flow(i,j,h,k) -
sum(j in NODES | exists(flow(j,i,h,k)) ) flow(j,i,h,k) = 1
! Capacity (robust) constraint
forall(i in NODES, j in NODES | exists(ARCCOST(i,j)) and ARCCOST(i,j) > 0)
RobustCap(i,j) :=
sum(h in NODES, k in NODES | h <> k) demand(h,k) * flow(i,j,h,k) <=
UNITCAP * capacity(i,j)
! Uncertainty set: all demands are nonnegative and constrained by
! total outgoing and incoming demand
forall(h in NODES, k in NODES | h <> k) demand(h,k) >= 0
forall(h in NODES) sum(k in NODES | h <> k) demand(h,k) <= DEM_OUT(h)
forall(h in NODES) sum(k in NODES | h <> k) demand(k,h) <= DEM_IN(h)
! Shortest path length
NetCost := sum(i in NODES, j in NODES | exists(ARCCOST(i,j)) and ARCCOST(i,j) > 0)
ARCCOST(i,j) * capacity(i,j)
!**** Solving ****
minimize(NetCost)
declarations
curNode: integer ! Local variable used in following the path of each demand
end-declarations
! Printing capacities
writeln("Robust solution has total cost ", getobjval)
forall(i in NODES, j in NODES | exists(capacity(i,j)) and capacity(i,j).sol > 0)
writeln("arc ", i, " -- ", j, ": ", capacity(i,j).sol, " units")
writeln("Paths:")
forall(h in NODES, k in NODES | h <> k) do
write("Demand ", h, " --> ", k, ": ")
curNode := h
write(h)
while(curNode <> k) do
forall(j in NODES | flow(curNode, j, h, k).sol > 0.5) do
write(" -- ", j)
curNode := j
end-do
end-do
writeln
end-do
writeln("Active demands at each arc:")
forall(i in NODES, j in NODES | exists(ARCCOST(i,j)) and ARCCOST(i,j) > 0 and
sum(h in NODES, k in NODES) getsol(demand(h,k), RobustCap(i,j)) > 0) do
write("Arc (", i, ",", j, "): ")
forall(h in NODES, k in NODES | getsol(demand(h,k), RobustCap(i,j)) > 0)
write(h, "-->", k, " (", getsol(demand(h,k), RobustCap(i,j)), "); ")
writeln
end-do
end-model
Input Data
Consider the network depicted in Figure Network topology, where each link represents two arcs in opposite directions. Table Maximum incoming/outgoing demand below reports the parameters specified in the data file vpn_data.dat describing the uncertainty set, i.e., the maximum incoming and outgoing traffic demands for each node of the network.
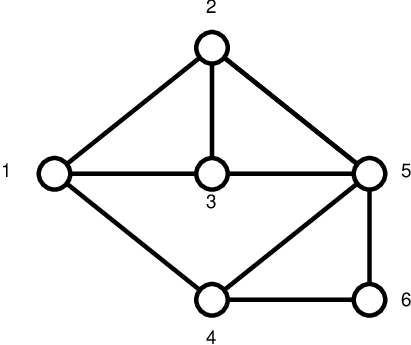
Figure 5: Network topology
| Node | Incoming | Outgoing |
|---|---|---|
| 1 | 120 | 105 |
| 2 | 34 | 95 |
| 3 | 35 | 82 |
| 4 | 101 | 102 |
| 5 | 78 | 76 |
| 6 | 75 | 140 |
Table Arc costs describes instead the arc cost for every arc (i,j) used in the network (a ``–'' means that no connection exists).
| i/j | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | – | 10 | 9 | 12 | – | – |
| 2 | 8 | – | 10 | – | 12 | – |
| 3 | 10 | 7 | – | – | 9 | – |
| 4 | 10 | – | – | – | 12 | 5 |
| 5 | – | 9 | 8 | 11 | – | 12 |
| 6 | – | – | – | 10 | 9 | – |
Results
For the example provided in vpn_data.dat, which describes a network of six nodes and 18 arcs, we obtain a design of total cost 566. Table Optimal arc capacity reports the number of units of capacity to be installed on each arc, while Table Optimal routes describes the path followed by each demand from source to destination.
| i/j | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | – | 2 | 2 | 13 | – | – |
| 2 | 5 | – | 0 | – | 0 | – |
| 3 | 5 | 0 | – | – | 0 | – |
| 4 | 10 | – | – | – | 4 | 4 |
| 5 | – | 0 | 0 | 4 | – | 0 |
| 6 | – | – | – | 7 | 0 | – |
| Source | Destination | Path | Source | Destination | Path |
|---|---|---|---|---|---|
| 1 | 2 | 1→2 | 4 | 1 | 4→1 |
| 1 | 3 | 1→3 | 4 | 2 | 4→1→2 |
| 1 | 4 | 1→4 | 4 | 3 | 4→1→3 |
| 1 | 5 | 1→4→5 | 4 | 5 | 4→5 |
| 1 | 6 | 1→4→6 | 4 | 6 | 4→6 |
| 2 | 1 | 2→1 | 5 | 1 | 5→4→1 |
| 2 | 3 | 2→1→3 | 5 | 2 | 5→4→1→2 |
| 2 | 4 | 2→1→4 | 5 | 3 | 5→4→1→3 |
| 2 | 5 | 2→1→4→5 | 5 | 4 | 5→4 |
| 2 | 6 | 2→1→4→6 | 5 | 6 | 5→4→6 |
| 3 | 1 | 3→1 | 6 | 1 | 6→4→1 |
| 3 | 2 | 3→1→2 | 6 | 2 | 6→4→1→2 |
| 3 | 4 | 3→1→4 | 6 | 3 | 6→4→1→3 |
| 3 | 5 | 3→1→4→5 | 6 | 4 | 6→4 |
| 3 | 6 | 3→1→4→6 | 6 | 5 | 6→4→5 |
The last part of the output shows, for each arc, the demands for which the uncertain values are non-zero in the worst case. Note that arcs such as (2,3) do not admit any nonzero demand simply because they are not used by the solution—the opponent has no incentive to increase the demand on such arcs.
Active demands at each arc: Arc (1,2): 1-->2 (34); Arc (1,3): 1-->3 (35); Arc (1,4): 1-->4 (101); 1-->5 (4); 2-->6 (67); 3-->5 (74); 3-->6 (8); Arc (2,1): 2-->1 (95); Arc (3,1): 3-->1 (82); Arc (4,1): 4-->1 (102); 5-->1 (18); 6-->2 (34); 6-->3 (35); Arc (4,5): 1-->5 (78); Arc (4,6): 1-->6 (75); Arc (5,4): 5-->1 (76); Arc (6,4): 6-->1 (106); 6-->2 (34);
© 2001-2025 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

