Selecting the right algorithm for a nonlinear problem - when to use the XPRS library instead of XSLP

This chapter focuses on the nonlinear capabilities of the FICO Xpress Optimizer. While Xpress XSLP is able to efficiently solve most nonlinear problems to local optimality, there are two reasons to use other Xpress libraries:

• Subclasses of nonlinear problems for which the Xpress Optimizer features specialized algorithms that are able to solve those problems more efficiently and in larger sizes. These are notably convex quadratic programming and convex quadratically constrained problems and their mixed integer counterparts.
• Situations in which a global optimum of a nonlinear problem is required. The functionality of FICO Xpress Global allows to also solve nonconvex QPs, MIQPs, NLPs and MINLPs to proven global optimality.

It is also possible to separate the convex quadratic information from the rest of XSLP, and let the Xpress XPRS optimizer handle those directly. Doing so is good modelling practice, but emphasis must be placed on that the Optimizer can only handle convex quadratic constraints, unless a license for FICO Xpress Global is present.

Convex Quadratic Programs (QPs)

Convex Quadratic Programming (QP) problems are an extension of Linear Programming (LP) problems where the objective function may include a second order polynomial. The FICO Xpress Optimizer can be used directly for solving QP problems (and the Mixed Integer version MIQP).

If there are no other nonlinearities in the problem, the XPRS library provides specialized algorithms for the solution of convex QP (and MIQP) problems, that are much more efficient than solving the problem as a general nonlinear problem with XSLP.

Convex Quadratically Constrained Quadratic Programs (QCQPs)

Quadratically Constrained Quadratic Programs (QCQPs) are an extension of the Quadratic Programming (QP) problem where the constraints may also include second order polynomials.

A QCQP problem may be written as:

minimize:	c1x1+...+cnxn+xTQ0x
subject to:	a11x1+...+a1nxn+xTQ1x	≤	b1
	...
	am1x1+...+amnxn+xTQmx	≤	bm
	l1≤x1≤u1,...,ln≤xn≤un

where any of the lower or upper bounds l_i or u_i may be infinite.

If there are no other nonlinearities in the problem, the XPRS library povides specialized algorithms for the solution of convex QCQP (and the integer counterpart MIQCQP) problems, that are much more efficient than solving the problem as a general nonlinear problem with XSLP.

Convexity

A fundamental property for nonlinear optimization problems, thus in QCQP as well, is convexity. A region is called convex, if for any two points from the region the connecting line segment is also part of the region.

The lack of convexity may give rise to several unfavorable model properties. Lack of convexity in the objective may introduce the phenomenon of locally optimal solutions that are not global ones (a local optimal solution is one for which a neighborhood in the feasible region exists in which that solution is the best). While the lack of convexity in constraints can also give rise to local optimums, they may even introduce non–connected feasible regions as shown in Figure Non-connected feasible regions.

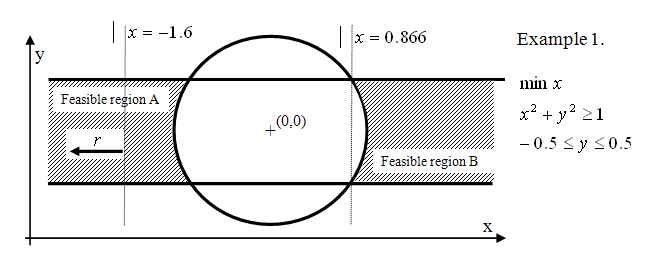
Figure 25.1: Non-connected feasible regions

In this example, the feasible region is divided into two parts. Over feasible region B, the objective function has two alterative local optimal solutions, while over feasible region A the objective is not even bounded.

For convex problems, each locally optimal solution is a global one, making the characterization of the optimal solution efficient.

Characterizing Convexity in Quadratic Constraints

A quadratic constraint of form

a₁x₁+...+a_nx_n+x^TQx≤b

defines a convex region if and only if Q is a so–called positive semi–definite (PSD) matrix.

A rectangular matrix Q is PSD by definition if for any vector (not restricted to the feasible set of a problem) x it holds that x^TQx≥0.

It follows that for greater or equal constraints

a₁x₁+...+a_nx_n-x^TQx≥b

the negative of Q shall be PSD.

A nontrivial quadratic equality constraint (one for which not every coefficient is zero) always defines a nonconvex region, therefore those must be modelled as XSLP structures.

There is no straightforward way of checking if a matrix is PSD or not. An intuitive way of checking this property, is that the quadratic part shall always only make a constraint harder to satisfy (i.e. taking the quadratic part away shall always be a relaxation of the original problem).

There are certain constructs however, that can easily be recognized as being non convex:

1. the product of two variables say xy without having both x² and y² defined;
2. having - x² in any quadratic expression in a less or equal, or having x² in any greater or equal row.

As a general rule, a convex quadratic objective and convex quadratic constraints are best handled by the XPRS library; while all nonconvex counterparts should be modelled as XSLP structures. It then depends on the application whether FICO Xpress Nonlinear is required (e.g., because of user functions) or FICO Xpress Global is the necessary solver (e.g., because a bound on the optimal objective is needed). Both use the same modelling API and, license and required features permitting, users can seamlessly switch between one solver or the other.