Start solution heuristic: Concurrent model clones using shared data structures

Topics covered in this section:

The example in this section shows how to use the concept of cloned models sharing data structures introduced in Section Shared data structures for cloned models for the implementation of a start solution heuristic for the classical jobshop scheduling problem. The generation of the start solutions involves concurrent solving of several instances of a subproblem that uses the same input data as the main problem and needs to communicate back the detailed results.

Example problem: jobshop scheduling

We wish to schedule the production of a set of jobs on a set of machines. Every job is produced by a sequence of tasks, each of these tasks is processed on a different machine with a specific given duration. A machine processes at most one job at a time. Tasks are non-preemptive (once started the processing cannot be interrupted). The objective is to minimize the total duration of the schedule, that is, the completion time of the last task, also referred to as makespan.

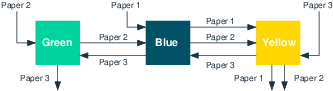
Figure 8: Jobshop example with 3 jobs (wallpapers) and 3 machines (colors)

This combinatorial problem is notoriously difficult to solve to optimality with mathematical programming approaches even for relatively small data instances. For practical purposes it is therefore quite a common practice to work with heuristics or some form of incomplete search, for example by stopping the solution algorithms after a certain laps of time. In such a case it is particularly important to be able to quickly compute good solutions and lower bound estimates.

Our start solution heuristic for the jobshop problem relies on the following idea: By solving single machine subproblems (sequencing the tasks that are processed on the same machine) we can generate partial solutions to the full jobshop problem that are loaded as start solutions into the MIP optimizer. This approach requires us to state and solve two distinct problems:

1. Several instances (one per machine) of a sequencing problem—these subproblems are independent and can therefore be formulated and solved concurrently
2. One instance of the full jobshop problem

Jobshop scheduling model

For the formulation of the jobshop problem we work with a set of JOBS, each composed of a series of TASKS that represent the processing of a job j on a specific resource m (from the set RESOURECS) with a known duration DUR_jm. The decision variables are the start and completion times of the tasks (start_jt and comp_jt respectively) and a set of binary variables y_mij for stating the sequence of tasks from two different jobs i and j on a resource m.

The objective function variable makespan is constrained to take the value of the latest completion time. We further need to state the order of tasks within every job (precedence relations) and the sequence of tasks on a given resouces (disjunctions between tasks).

Objective:

minimize makespan

Decision variables:

∀ j ∈ JOBS, t ∈ TASKS: start_jt,comp_jt ∈ [0,MAXTIME]
∀ m ∈ RESOURCES, i<j ∈ JOBS: y_mij ∈ {0,1}

Precedence relations:

∀ j ∈ JOBS: makespan ≥ start_j,NBRES + DUR_j,NBRES
∀ j ∈ JOBS, t ∈ TASKS-{NBRES}: start_jt + DUR_jt ≤ start_j,t+1

Disjunctions between tasks on same machine:

∀ m ∈ RESOURCES, i<j ∈ JOBS: start_i,RESmi +DUR_i,RESmi ≤ start_j,RESmj + M·y_mij
start_j,RESmj +DUR_j,RESmj ≤ start_i,RESmi + M·(1-y_mij)

Linking start and completion times:

∀ j ∈ JOBS, t ∈ TASKS: start_jt + DUR_jt = comp_jt

Single machine sequencing subproblem

The sequencing problem on a specific machine m is expressed via a separate set of binary decision variables rank_jk that indicate whether the task from job j is processed in position k on this resource. The start time of the task in position k is expressed by tstart_k. We take into account the release date REL_j (sum of the durations of preceding tasks) and the total duration (processing time DUR_jm of the task itself and duration DURSUCC_j of all its successors within the job) for calculating a job completion time jcomp_j, the maximum of which (= makespan) is to be minimized. This makespan of the individual subproblems provides a lower bound on the makespan of the full jobshop problem.

Objective:

minimize makespan

Decision variables:

∀ j,k ∈ JOBS: rank_jk ∈ {0,1}
∀ j ∈ JOBS: jcomp_j ∈ [0,MAXTIME]
∀ k ∈ JOBS: tstart_k ∈ [0,MAXTIME]

One job per position, one position per job:

∀ k ∈ JOBS: ∑_{j ∈ JOBS} rank_jk = 1
∀ j ∈ JOBS: ∑_{k ∈ JOBS} rank_jk = 1

Sequence of jobs:

∀ k ∈ 1,...,NJOBS-1: tstart_k+1 ≥ tstart_k + ∑_{j ∈ JOBS} DUR_jm·rank_jk

Release dates for start times:

∀ k ∈ JOBS: tstart_k ≥ ∑_{j ∈ JOBS} REL_j·rank_jk

Completion times:

∀ k ∈ JOBS: jcomp_k = tstart_k + ∑_{j ∈ JOBS} (DUR_jm+DURSUCC_j)·rank_jk
makespan ≥ jcomp_k

Implementation

The implementation of a model that starts submodels in the form of clones in order to work with shared data structures needs to contain the code for both, controlling model and submodels, in a single file.

The main model logic with all declarations of entities and subroutines is shown below: the actual model is contained in the last if statement that decides which subroutines to execute depending on whether the model is run as the controlling model (solving the full scheduling problem) or as a clone that solves a sequencing subproblem.

model "Job shop - Clone"
 uses "mmxprs", "mmjobs", "mmsystem"

 parameters
  DATAFILE = "mt10.dat"           ! Muth and Thompson 10x10 instance
  MACH = 1                        ! Subproblem identifier
  MAXTHRD = 2                     ! Max number of parallel threads for one inst.
 end-parameters

 declarations
 ! **** Shared data
  NBJOBS: shared integer                     ! Number of jobs
  NBRES: shared integer                      ! Number of resources
  JOBS: shared range                         ! Set of jobs
  TASKS: shared range                        ! Set of tasks (one per machine)
  TASKSM1: shared range                      ! Set of tasks without last
  RESOURCES: shared range                    ! Set of resources
  DUR: shared array(JOBS,TASKS) of integer          ! Durations of tasks
  RESIND: shared array(RESOURCES,JOBS) of integer   ! Task index per resource
  MAXDUR: shared array(RESOURCES) of integer
  BIGM: integer                              ! Used in formulation of main prob

  cutoff,starttime: real                     ! Temp. value used in main problem
  bbindex: integer                           ! Temp. value used in main problem

 ! **** Declarations for main problem
  start: array(JOBS,TASKS) of mpvar          ! Start times of tasks
  comp: array(JOBS,TASKS) of mpvar           ! Completion times of tasks
  makespan: mpvar                            ! Schedule completion time
  y: dynamic array(RESOURCES,JOBS,JOBS) of mpvar  ! Disjunction variables

 ! **** Declarations for sequencing subproblems
  heursol: dynamic array(set of mpvar) of real
  rank: array(JOBS,JOBS) of mpvar            ! =1 if job j at position k
  jcomp,tstart: array(JOBS) of mpvar         ! Start time of job at position k

 ! **** Model and solution handling
  SeqMod: array(RESOURCES) of Model             ! Models
  NOSOL=2                                       ! "No sol found" event
  NEWSOL=3                                      ! "Solution found" event
  pos: shared array(RESOURCES,JOBS) of integer  ! Subproblem solutions
  Makespan: shared array(RESOURCES) of real     ! Subproblem makespan

 ! **** Subroutines
  procedure readdata
  procedure sequencemachine(m:integer)
  procedure disjunctiveconstraints(m:integer)
  procedure solvemain
  procedure printsol
 end-declarations

!*********************************Model body*******************************

 if getparam("sharingstatus")<=0 then
   readdata
   solvemain
   printsol
 else
   sequencemachine(MACH)
 end-if

end-model  

Jobshop problem

The controlling model starts with the data input via the following subroutine readdata, all input data items are a marked as shared meaning that they are available within clones of this model:

 procedure readdata
   initializations from DATAFILE
     NBJOBS NBRES
   end-initializations
   JOBS := 1..NBJOBS; finalize(JOBS)
   TASKS := 1..NBRES ; finalize(TASKS)
   TASKSM1 := 1..NBRES-1  ; finalize(TASKSM1)
   RESOURCES := 0..NBRES-1 ; finalize(RESOURCES)

   declarations
     taskUse: array(JOBS,TASKS) of integer   ! Resource use of tasks
   end-declarations

   initializations from DATAFILE
     taskUse  DUR as "taskDuration"
   end-initializations

   forall(m in RESOURCES,j in JOBS,t in TASKS | taskUse(j,t) = m) RESIND(m,j):=t

   BIGM:=sum(j in JOBS,t in TASKS) DUR(j,t)    ! Some (sufficiently) large value
   forall(m in RESOURCES) MAXDUR(m):=sum(j in JOBS) DUR(j,RESIND(m,j))
 end-procedure

The implementation of the jobshop problem is contained in the following subroutine that defines the problem, creates and runs the concurrent sequencing subproblems as clones, and transforms the solutions returned by these into the required from for adding them as (partial) start solutions into the full problem.

 procedure solvemain
  ! Precedence constraints between last task of every job and makespan
   forall(j in JOBS) makespan >= start(j,NBRES) + DUR(j,NBRES)

  ! Precedence constraints between the tasks of every job
   forall(j in JOBS,t in TASKSM1)
     start(j,t) + DUR(j,t) <= start(j,t+1)

  ! Disjunctions
   forall(r in RESOURCES) disjunctiveconstraints(r)

  ! Linking start and completion times
   forall(j in JOBS,t in TASKS) start(j,t)+DUR(j,t) = comp(j,t)

  ! Bound on latest completion time
   makespan <= BIGM

   starttime:=gettime

  ! Solve the single machine sequencing problems
   forall(m in RESOURCES) do
     load(SeqMod(m))                      ! Clone the current model
     SeqMod(m).uid:= m
     setworkdir(SeqMod(m), ".")
     run(SeqMod(m), "MACH="+m +",MAXTHRD="+1)
   end-do
   tct:=0
   while (tct<NBRES) do
     wait                                 ! Wait for the next event
     Msg:= getnextevent                   ! Get the event
     mid:= Msg.fromuid                    ! Get model number of sender
     if getclass(Msg)=NEWSOL then         ! Get the event class
       if Makespan(mid)>cutoff then
         cutoff:= Makespan(mid);
         bbindex:=mid
       end-if
       writeln_("*** (", gettime-starttime, "s) Machine ", mid, ": ", Makespan(mid))

       forall(i,j in JOBS | i<j ) heursol(y(mid,i,j)):= if(pos(mid,i)<pos(mid,j), 0, 1)
       loadprob(makespan)                 ! Make sure problem is loaded
       id:="mach"+mid
       addmipsol(id,heursol)              ! Load the heuristic solution
       writeln_("Loaded solution Id: ", id)
       setcallback(XPRS_CB_SOLNOTIFY, ->solnotify)
       delcell(heursol)                   ! Delete saved solution values
     elif getclass(Msg)=NOSOL then
       writeln_("Subproblem ", mid, " has no solution. Stopping")
       exit(1)
     else
       tct+=1
       unload(SeqMod(mid))                ! Delete subproblem
     end-if
   end-do

   writeln_("(", gettime-starttime, "s) Best lower bound: ", cutoff)

  ! Re-inforce use of user solutions by local search MIP heuristics
   setparam("XPRS_USERSOLHEURISTIC", 3)

  ! Set a time limit
   setparam("XPRS_SOLTIMELIMIT", 5)

  ! Solve the problem: minimize latest completion time
   minimize(makespan)
 end-procedure

! **** Callback reporting the status of loaded solutions ****
 procedure solnotify(id:string, status:integer)
   writeln_("Optimiser loaded solution ", id, " status=", status)
 end-procedure

The subroutine disjunctiveconstraints defines the disjunctions between tasks on the same resource—by moving the definition of these constraints into a separate subroutine it becomes easy to experiment with alternative formulations for these constraints (such as by using indicator constraints in place of the big-M construct employed in the version shown here).

 procedure disjunctiveconstraints(m:integer)
   forall(i,j in JOBS | i<j) do
     create(y(m,i,j))
     y(m,i,j) is_binary               !=1 if i>>j, =0 if i<<j

     start(i,RESIND(m,i))+DUR(i,RESIND(m,i)) <=
       start(j,RESIND(m,j))+BIGM*y(m,i,j)
     start(j,RESIND(m,j))+DUR(j,RESIND(m,j)) <=
       start(i,RESIND(m,i))+BIGM*(1-y(m,i,j))
    end-do
 end-procedure   

The implementation of the jobshop problem is completed with some solution display at the end of the solving of the full problem:

 procedure printsol
   writeln_("(", gettime-starttime, "s) Total completion time: ", getobjval)
   forall(j in JOBS) write(strfmt(j,8))
   writeln
   forall(m in RESOURCES) do
     write(strfmt((m+1),-3))
     forall(j in JOBS)
       if(DUR(j,RESIND(m,j))>0) then
         write(formattext("%4d-%3d", round(getsol(start(j,RESIND(m,j)))),
              round(getsol(start(j,RESIND(m,j)))+DUR(j,RESIND(m,j)))))
       else
         write(strfmt(" ",6))
       end-if
     writeln
   end-do
 end-procedure 

Sequencing subproblem

The implementation of the sequencing subproblem is provided by the following subroutine that terminates by sending an event that notifies the controlling model of the solving status (indicating whether a subproblem solution is available):

 procedure sequencemachine(m:integer)
  ! One job per position
   forall(k in JOBS) sum(j in JOBS) rank(j,k) = 1

  ! One position per job
   forall(j in JOBS) sum(k in JOBS) rank(j,k) = 1

  ! Sequence of jobs
   forall(k in 1..NBJOBS-1)
     tstart(k+1) >=
       tstart(k) + sum(j in JOBS) DUR(j,RESIND(m,j))*rank(j,k)

  ! Start times (release date = min total duration for preceding tasks)
   forall(j in JOBS) REL(j):= sum(t in 1..RESIND(m,j)-1) DUR(j,t)
   forall(j in JOBS) DURSUCC(j):= sum(t in RESIND(m,j)+1..NBRES) DUR(j,t)

   forall(k in JOBS) tstart(k) >= sum(j in JOBS) REL(j)*rank(j,k)

  ! Completion times
   forall(k in JOBS) jcomp(k) =
     tstart(k) + sum(j in JOBS) (DUR(j,RESIND(m,j))+DURSUCC(j))*rank(j,k)

   forall(j,k in JOBS) rank(j,k) is_binary

  ! Objective function: minimize latest completion time
   forall(k in JOBS) makespan >= jcomp(k)

  ! Solve the problem
   minimize(makespan)

  ! Solution reporting
   if getprobstat=XPRS_OPT then
    ! writeln_("*** Machine ", m, ": ", getobjval)
     forall(j in JOBS) pos(m,j):= round(sum(k in JOBS) k*rank(j,k).sol)
     Makespan(m):=getobjval

    ! Send "solution found" signal
     send(NEWSOL, getobjval)
   else
     send(NOSOL, 0)
   end-if
 end-procedure 

Results

For the datasets used for testing (such as the much studied MT10 instance from [FT63]) most often the MIP heuristics are only able to complete few of the partial solutions to a full solution, but where this is possible this solution usually is better than any initial solution detected by the default algorithms.

Several other implementation variants are available for this start solution algorithm:

1. Instead of starting model clones for solving the sequencing subproblems these could simply be treated as multiple problems that are solved sequentially within a single model. All problems and data simply reside within a single model in this case, so there is no need to employ any mechanism for sharing data. Furthermore, only a single subproblem is active in the solver at any time, hence limiting the amount of resouces (memory, licenses) that are in concurrent use. An implementation example is provided in the file jobshopas.mos.
2. As for the examples discussed in the preceding sections of this paper, concurrent solving with submodels can be implemented with a separate file for every problem (so one main model file, jobshopasp.mos, and one submodel file, jobseq.mos, that is loaded for each subproblem instance to be processed in parallel). In this case, data are exchanged between the parent model and its descendants via the shared memory I/O driver of mmjobs. As opposed to the implementation relying on model clones this version could be extended to work with several distinct Mosel instances for processing the submodels.

With all three implementation variants we are solving the same sequencing subproblems and will therefore obtain the same (partial) start solutions. When solving subproblems concurrently our implementation processes the results as soon as they become available, so the order with which start solutions are added and as a consequence the order in which they are processed by the solver is to some extend non-deterministic and may result in diverging behaviour of the solution algorithms. With sequential execution the order of adding the user solution information is always the same.