Solving several model instances in parallel
Topics covered in this section:
In this section we show how to execute several models in parallel and communicate solution information among these models. This scheme may be particularly interesting when working with Mosel on a multi-processor machine, e.g. by starting a number of models that corresponds to the available number of processors.
Our idea is to run several instances (different only by the parameterization of the solution algorithm) of the same MIP model concurrently and to stop the entire run when the first model has finished. If the different solution algorithms are complementary in the sense that some quickly produce (good) solutions and others are better at proving optimality once the best solution is found then one may reasonably expect an additional synergy effect from exchanging solution updates during the MIP search.
To implement this scheme, we define a main model that starts the model runs and coordinates the solution updates, and a parameterizable child model that is loaded and run with the desired number of versions. The child models all use the same solver (Xpress Optimizer) but it would equally be possible to use a different solver for some of the child models, provided it defines the necessary functionality for interacting with the search.
Example problem: economic lot sizing
Economic lot sizing (ELS) considers production planning over a given planning horizon, in our example a range of time periods TIMES = 1,...,T. In every period t, there is a given demand DEMANDpt for every product p (p ∈ PRODUCTS) that must be satisfied by the production in this period and by inventory carried over from previous periods.
A set-up cost SETUPCOSTt is associated with production in a period, and the total production capacity per period, CAPt, is limited. The unit production cost PRODCOSTpt per product and time period is also given. There is no inventory or stock-holding cost.
We introduce the decision variables producept for the amount of product p made in period t and the binary variables setuppt indicating whether a setup takes place for product p in period t (setuppt = 1) or not (setuppt = 0).
We may then formulate the following mathematical model for this problem:
| ∑ |
| t ∈ TIMES |
| ∑ |
| p ∈ PRODUCTS |
| ∑ |
| p ∈ PRODUCTS |
∀ p ∈ PRODUCTS, t ∈ TIMES:
| t |
| ∑ |
| s = 1 |
| t |
| ∑ |
| s = 1 |
∀ p ∈ PRODUCTS, t ∈ TIMES: producept ≤ DptT · setuppt
∀ t ∈ TIMES:
| ∑ |
| p ∈ PRODUCTS |
∀ p ∈ PRODUCTS, t ∈ TIMES: setuppt ∈ {0,1}, producept ≥ 0
The objective function is to minimize the total cost. The constraints in the second line formulate the requirement that the production of p in periods 0 to t must satisfy the total demand for this product during this period of time. The next set of constraints establish the implication `if there is production during t then there is a setup in t' where Dptl stands for the demand of product p in periods t to l. The production capacity per period t is limited. And finally, the setuppt variables are binaries.
Cutting plane algorithm
A well-known class of valid inequalities for ELS are the so-called (l,S)-inequalities [PW94]. If Dptl denotes the total demand of p in periods t to l, then for each period l and each subset of periods S of 1 to l, the (l,S)-inequality is
| l |
| ∑ |
| t = 1 | t ∈ S |
| l |
| ∑ |
| t = 1 | t ∉ S |
It says that actual production producept in the periods included in S plus the maximum potential production Dptl · setuppt in the remaining periods (those not in S) must at least equal the total demand in periods 1 to l.
It is possible to develop the following cutting plane algorithm based on these (l,S)-inequalities:
- Solve the LP.
- Identify violated (l,S)-inequalities by testing violations of
min(producept, Dptl · setuppt) ≥ Dp1ll ∑ t = 1 - Add violated inequalities as cuts to the problem.
- Re-solve the LP problem.
There are numerous options for how to configure this algorithm. For instance:
- Generation of cuts only in the root node or also during the search (Cut-and-Branch versus Branch-and-Cut).
- Number of cut generation passes at a node (e.g. one pass or looping around steps 2.-4. until no more cuts are generated).
- Search tree depth for cut generation (up to a given depth or at all nodes).
- Exclusive use of (l,S)-cuts or combination with others (e.g. default cuts generated by the solver).
The implementation of the (l,S)-cut generation algorithm shown below may be configured to generate cuts at the top node only (TOPONLY = true) and to generate one or several rounds of cuts (SEVERALROUNDS = true).
Implementation
With mmjobs events are always sent between parent – child pairs, not directly from one child to another. The 'solution found' message therefore needs to be sent to the parent model that then passes on this message to all other child models.
Another point that should be stressed is the fact that we only compile the ELS model file once, but the number of instances loaded into memory needs to correspond to the number of child models we wish to run.
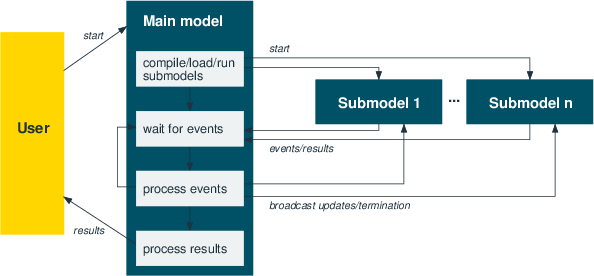
Figure 6: Parallel submodels coordinated by events
Main model
The main model compiles, loads and runs the child models and coordinates the solution updates. Some care must be taken with the solution updates since new solutions that are reported are not guaranteed to be better than others previously reported by other child models. For instance, if two models find solutions almost at the same time, the first solution that reaches the parent may be the better one and it must not be overridden by the next.
For a nice solution display at the end, the main model also reads in parts of the problem data from file.
model "Els main"
uses "mmjobs"
parameters
DATAFILE = "els5.dat"
T = 45
P = 4
end-parameters
declarations
RM = 0..5 ! Range of models
TIMES = 1..T ! Time periods
PRODUCTS = 1..P ! Set of products
solprod: array(PRODUCTS,TIMES) of real ! Sol. values for var.s produce
solsetup: array(TIMES) of real ! Sol. values for var.s setup
DEMAND: array(PRODUCTS,TIMES) of integer ! Demand per period
modELS: array(RM) of Model ! Models
NEWSOL = 2 ! Identifier for "sol. found" event
Msg: Event ! Messages sent by models
params: text ! Submodel runtime parameters
end-declarations
! Compile, load, and run models M1 and M2
M1:= 1; M2:=2
res:= compile("elsp.mos") ! Compile the submodel
load(modELS(M1), "elsp.bim") ! Load submodels
load(modELS(M2), "elsp.bim")
forall(m in RM) modELS(m).uid:= m ! Store the model indices
setmodpar(params, "DATAFILE", DATAFILE) ! Configure submodel parameters
setmodpar(params, "T", T); setmodpar(params, "P", P)
! Start submodel runs
setmodpar(params, "ALG", M1); run(modELS(M1), params)
setmodpar(params, "ALG", M2); run(modELS(M2), params)
objval:= MAX_REAL
algsol:= -1; algopt:= -1
repeat
wait ! Wait for the next event
Msg:= getnextevent ! Get the event
if getclass(Msg)=NEWSOL then ! Get the event class
if getvalue(Msg) < objval then ! Value of the event (= obj. value)
algsol:= getfromuid(Msg) ! UID of model sending the event
objval:= getvalue(Msg)
writeln_("Improved solution ", objval, " found by model ", algsol)
forall(m in RM | m <> algsol) send(modELS(m), NEWSOL, objval)
else
writeln_("Solution ", getvalue(Msg), " found by model ", Msg.fromuid)
end-if
end-if
until getclass(Msg)=EVENT_END ! A model has finished
algopt:= getfromuid(Msg) ! Retrieve ID of terminated model
forall(m in RM) stop(modELS(m)) ! Stop all running models
if algsol=-1 then
writeln_("No solution available")
exit(1)
else ! Retrieve the best solution from shared memory
initializations from "bin:shmem:sol"+algsol
solprod
solsetup
end-initializations
initializations from DATAFILE
DEMAND
end-initializations
! Solution printing
writeln_("Best solution found by model ", algsol)
writeln_("Optimality proven by model ", algopt)
writeln_("Objective value: ", objval)
write_("Period setup ")
forall(p in PRODUCTS) write(strfmt(p,-7))
forall(t in TIMES) do
write("\n ", strfmt(t,2), strfmt(solsetup(t),8), " ")
forall(p in PRODUCTS) write(strfmt(solprod(p,t),3), " (",DEMAND(p,t),")")
end-do
writeln
end-if
end-model In this implementation we save the model index used in our model as UID (user index) information with each model object. Whenever a child model sends an event to the parent model, we retrieve its UID (with function getfromuid) to identify the corresponding submodel in our model and use this information for solution printing later on.
ELS model
The ELS child model is written in such a way that the model can be executed separately. In particular, every model performs the complete initialization of its data from file, a task that for greater efficiency could be reserved to the parent model, communicating data via shared memory to the child models (however, in our example data handling time is negligible compared to the running time of the solution algorithms).
The main part of the ELS model contains the definition of the model itself and the selection of the solution algorithm:
model Els
uses "mmxprs","mmjobs"
parameters
ALG = 0 ! Default algorithm: no user cuts
DATAFILE = "els4.dat"
T = 60
P = 4
end-parameters
forward procedure tree_cut_gen
forward function cb_node: boolean
forward function cb_updatebnd: boolean
forward procedure cb_intsol
declarations
NEWSOL = 2 ! "New solution" event class
EPS = 1e-6 ! Zero tolerance
TIMES = 1..T ! Time periods
PRODUCTS = 1..P ! Set of products
DEMAND: array(PRODUCTS,TIMES) of integer ! Demand per period
SETUPCOST: array(TIMES) of integer ! Setup cost per period
PRODCOST: array(PRODUCTS,TIMES) of real ! Production cost per period
CAP: array(TIMES) of integer ! Production capacity per period
D: array(PRODUCTS,TIMES,TIMES) of integer ! Total demand in periods t1 - t2
produce: array(PRODUCTS,TIMES) of mpvar ! Production in period t
setup: array(TIMES) of mpvar ! Setup in period t
solprod: array(PRODUCTS,TIMES) of real ! Sol. values for var.s produce
solsetup: array(TIMES) of real ! Sol. values for var.s setup
Msg: Event ! An event
end-declarations
initializations from DATAFILE
DEMAND SETUPCOST PRODCOST CAP
end-initializations
forall(p in PRODUCTS,s,t in TIMES) D(p,s,t):= sum(k in s..t) DEMAND(p,k)
! Objective: minimize total cost
MinCost:= sum(t in TIMES) (SETUPCOST(t) * setup(t) +
sum(p in PRODUCTS) PRODCOST(p,t) * produce(p,t) )
! Production in period t must not exceed the total demand for the
! remaining periods; if there is production during t then there
! is a setup in t
forall(t in TIMES)
sum(p in PRODUCTS) produce(p,t) <= sum(p in PRODUCTS) D(p,t,T) * setup(t)
! Production in periods 0 to t must satisfy the total demand
! during this period of time
forall(p in PRODUCTS,t in TIMES)
sum(s in 1..t) produce(p,s) >= sum (s in 1..t) DEMAND(p,s)
! Capacity limits
forall(t in TIMES) sum(p in PRODUCTS) produce(p,t) <= CAP(t)
forall(t in TIMES) setup(t) is_binary ! Variables setup are 0/1
setparam("zerotol", EPS/100) ! Set Mosel comparison tolerance
SEVERALROUNDS:=false; TOPONLY:=false
case ALG of
1: do
setparam("XPRS_CUTSTRATEGY", 0) ! No cuts
setparam("XPRS_HEUREMPHASIS", 0) ! No heuristics
end-do
2: do
setparam("XPRS_CUTSTRATEGY", 0) ! No cuts
setparam("XPRS_HEUREMPHASIS", 0) ! No heuristics
setparam("XPRS_PRESOLVE", 0) ! No presolve
end-do
3: tree_cut_gen ! User branch&cut (single round)
4: do ! User branch&cut (several rounds)
tree_cut_gen
SEVERALROUNDS:=true
end-do
5: do ! User cut&branch (several rounds)
tree_cut_gen
SEVERALROUNDS:=true
TOPONLY:=true
end-do
end-case
! Parallel setup
setcallback(XPRS_CB_PRENODE, ->cb_updatebnd) ! Node pre-treatment callback
setcallback(XPRS_CB_INTSOL, ->cb_intsol) ! Integer solution callback
! Solve the problem
minimize(MinCost)
end-model The procedure tree_cut_gen sets up a user cut generation routine, configurable to generate cuts only at the top node of the branch-and-bound search (TOPONLY) or to execute one or several cut generation iterations per node (SEVERALROUNDS). The definition of the cut generation routine cb_node itself is left out here.
procedure tree_cut_gen
setparam("XPRS_HEUREMPHASIS", 0) ! Switch heuristics off
setparam("XPRS_CUTSTRATEGY", 0) ! Switch automatic cuts off
setparam("XPRS_PRESOLVE", 0) ! Switch presolve off
setparam("XPRS_EXTRAROWS", 5000) ! Reserve extra rows in matrix
setcallback(XPRS_CB_OPTNODE, ->cb_node) ! Define the optnode callback
end-procedure The communication between concurrently running child models has two parts: (a) any integer solution found must be saved and comunicated to the parent model and (b) bound updates sent by the controlling model must be incorporated into the search. Xpress Optimizer provides a specific integer solution callback for saving solutions into user structures. An obvious place for bound updates in nodes is the cut-manager callback function. However, this function being already in use for other purposes with certain settings of the algorithm, we employ a different callback function that also gets called at every node, the node pre-treatment callback.
! **** Update cutoff value ****
function cb_updatebnd: boolean
if not isqueueempty then
repeat
Msg:= getnextevent
until isqueueempty
newcutoff:= getvalue(Msg)
if newcutoff < getparam("XPRS_MIPABSCUTOFF") then
setparam("XPRS_MIPABSCUTOFF", newcutoff)
end-if
if (newcutoff < getparam("XPRS_LPOBJVAL")) then
returned:= true ! Node becomes infeasible
end-if
end-if
end-function
! **** Store and communicate new solution ****
procedure cb_intsol
objval:= getparam("XPRS_LPOBJVAL") ! Retrieve current objective value
cutoff:= getparam("XPRS_MIPABSCUTOFF")
if(cutoff > objval) then
setparam("XPRS_MIPABSCUTOFF", objval)
end-if
! Get the solution values
forall(t in TIMES) do
forall(p in PRODUCTS) solprod(p,t):=getsol(produce(p,t))
solsetup(t):=getsol(setup(t))
end-do
! Store the solution in shared memory
initializations to "bin:shmem:sol"+ALG
solprod
solsetup
end-initializations
! Send "solution found" signal
send(NEWSOL, objval)
end-procedure The bound update callback function checks whether the event queue contains any events, if this is the case, it takes all events from the queue and sets the value of the last event as the new cutoff value. The rationale behind the loop for emptying the event queue is that the parent model may have sent several improved solution values since the last check, the best value is always the one sent last, that is, the last in the queue.
The integer solution callback writes the solution values to shared memory, adding the identifier of the model (= value of ALG). The latter ensures that two child models that possibly write out their solution at the same time do not use the same memory area.
Results
A run with two models may generate a log similar to the following one (note that the model that terminates the search is not the same that has found the optimal solution).
Improved solution 1283 found by model 2 Improved solution 1250 found by model 2 Improved solution 1242 found by model 1 Improved solution 1236 found by model 2 Improved solution 1234 found by model 2 Best solution found by model 2 Optimality proven by model 1 Objective value: 1234
© 2001-2026 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

