Problem Types

Topics covered in this chapter:

FICO Xpress is a powerful optimization tool for solving Mathematical Optimization problems. FICO Xpress Global allows users to formulate problems with nonlinear, potentially non-convex, constraints and objective over continuous and integer variables and solve them to proven global optimality.

Mathematical Optimization problems are usually classified according to the types of decision variables, constraints, and objective function. This section will briefly introduce some important types of problems, focusing on distinctions important to FICO Xpress Global.

Linear vs. Nonlinear Problems

The field of Mathematical Optimization has its roots in solving linear programming (LP) problems. In this type of problem, all constraints and the objective function are linear expressions of the decision variables. The FICO Xpress Optimizer implements very efficient algorithms for LP solving, namely the simplex, the barrier and the hybrid gradient methods. Computational theory confirms that we can solve LPs efficiently (in polynomial time) and precisely.

Nonlinearity makes the matter more complicated. An optimization problem is referred to as a nonlinear program (NLP) as soon as at least one constraint or the objective function contains a nonlinear expression (e.g., a polynomial or a trigonometric function). For computational complexity and the required solution methods, it does not, in general, make a difference how many of the constraints are nonlinear. However, many nonlinear problems in practice consist of a strong linear core with only a few additional nonlinear constraints. This can be favorable for the convergence speed of the solver. Concerning efficiency, on both the theoretical and the practical side, the most important distinction is between convex and non-convex nonlinearities; see the next section.

Finally, note that algorithms for nonlinear problems approximate the solution up to a certain precision. While small numerical violations may or may not occur in linear problems due to numerical issues, in nonlinear optimization, tiny violations both on the dual and the primal side are almost always to be expected.

Convex vs. Non-Convex Problems

A set (e.g., the feasible region of an optimization problem) is called convex when for any two points in the set, the line connecting them is entirely contained in the set itself. For example, a disc is convex, and a heart shape is non-convex, see Figure 3.1. This directly relates to a very crucial property for optimization. Every local optimum is a global optimum when optimizing a convex function over a convex set. This makes convex optimization much easier, both theoretically and practically. Local optima may occur when either the objective function or the feasible region described by the constraints are non-convex.

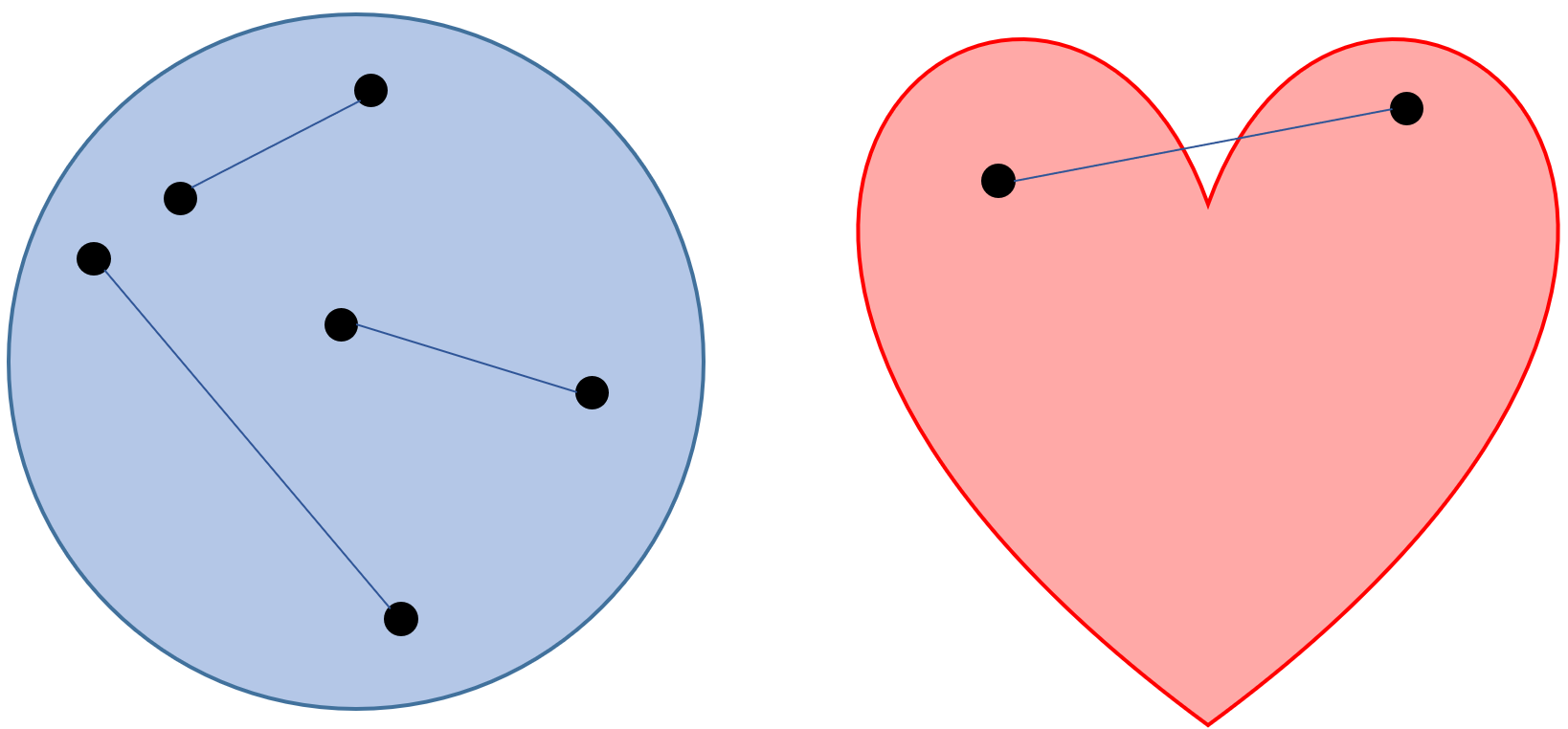
Figure 3.1: A convex and a non-convex set

Even more challenging, a feasible set described by non-convex constraints might be disconnected. Consider the situation in Figure 3.2. We see the feasible region of a non-convex NLP, defined by some variable bounds and two inequalities that contain a sine term. The feasible region, shaded in dark blue, consists of six distinct feasible components. When optimizing the red, linear objective function, there are nine local (including one global) optima: the red points.

While convex optimization is comparably easy (solvable in polynomial time, up to a certain precision), non-convex optimization is theoretically even harder than MIP. For non-convex problems, it is impossible to formulate guidelines for expected runtimes. In extreme cases, even non-convex NLPs with only a handful of variables can take an eternity to solve to global optimality. In contrast, others with thousands of constraints and variables might be solvable within seconds.

Note that FICO Xpress Global is different from FICO Xpress Nonlinear, whose documentation can be found here. FICO Xpress Nonlinear targets finding locally optimal solutions for non-convex problems. FICO Xpress Global finds globally optimal solutions for non-convex problems. For convex problems, both will find globally optimal solutions. It cannot be readily determined a priori which of the two solvers will be superior in performance since both tackle the same problem with somewhat different approaches. For a particular convex problem, it is worth checking both independently. These considerations hold both for the continuous and mixed-integer case.

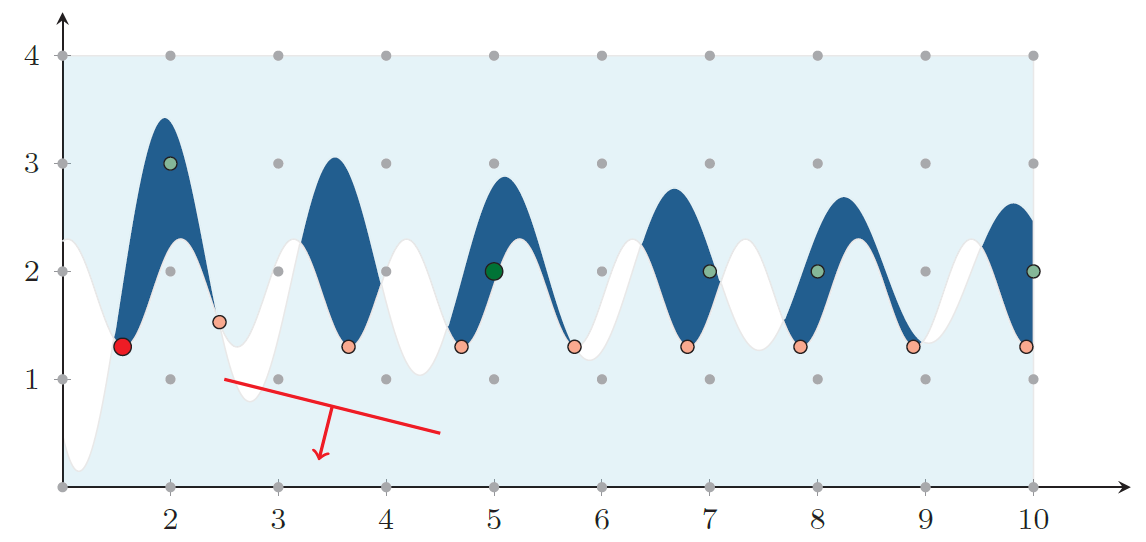
Figure 3.2: A non-convex (MI)NLP

Continuous vs. Mixed-Integer Problems

As in the linear case, an important distinction is between problems with purely continuous variables and those for which at least one variable is integer. Problems that are both nonlinear and have integer variables are called MINLPs, mixed-integer nonlinear programs. As in the LP/MIP case, discrete variables make convex nonlinear problems harder to solve but are often imperative for practical applications. Curiously, a non-convex MINLP can be easier to solve than its continuous counterpart; nevertheless, non-convex MINLPs are among the hardest optimization problems that occur in practice. As an example of a non-convex MINLP, consider again Figure 3.2, now assuming integrality conditions for both variables. The MINLP has five feasible solutions, indicated in green, with the globally optimal one being "in the middle", at (5,2).

Note that FICO Xpress Global will solve non-convex MINLPs to proven global optimality, whereas there are many solvers that can only guarantee local optimality for non-convex NLPs and have no optimality guarantees for non-convex MINLPs.

Even though we did not mention them explicitly yet, FICO Xpress Global supports other types of MIP entities, most importantly special-ordered sets (SOSs) and semi-continuous variables. Further, indicator constraints can be added to MINLPs.