Constraints
Topics covered in this chapter:
- Constraint handling
- Arithmetic constraints
- all_different: Sudoku
- abs and distance: Frequency assignment
- element: Sequencing jobs on a single machine
- occurrence: Sugar production
- distribute: Personnel planning
- implies: Paint production
- equiv: Location of income tax offices
- cycle: Paint production
- Generic binary constraints: Euler knight tour
- Symmetry breaking: scenes allocation problem
This chapter contains a collection of examples demonstrating the use of Xpress Kalis from Mosel for solving different types of (optimization) problems. The first section shows different ways of defining and posting constraints for simple linear constraints. The following sections each introduce a new constraint type. Since most examples use a combination of different constraints, the following list may help in finding examples of the use of a certain constraint type quickly.
- arithmetic: linear disequality: A first model (meeting.mos), Data input from file (i4exam*.mos), distribute: Personnel planning (persplan.mos); linear equality/inequality: element: Sequencing jobs on a single machine (b4seq*_ka.mos), occurrence: Sugar production (i1assign_ka.mos), implies: Paint production (b5paint*_ka.mos), equiv: Location of income tax offices (j5tax_ka.mos), User-defined enumeration strategies (i1assign_ka.mos), Precedences (b1stadium_ka.mos); nonlinear: Arithmetic constraints
- all_different: all_different: Sudoku (sudoku_ka.mos), element: Sequencing jobs on a single machine (b4seq_ka.mos), implies: Paint production (b5paint*_ka.mos), abs and distance: Frequency assignment (freqasgn.mos), distribute: Personnel planning (persplan.mos), Generic binary constraints: Euler knight tour (eulerkn*.mos), User-defined enumeration strategies (i1assign_ka.mos)
- abs / distance: abs and distance: Frequency assignment (freqasgn.mos)
- cumulative: Cumulative scheduling: discrete resources (d4backup2_ka.mos)
- cycle: cycle: Paint production (b5paint3_ka.mos)
- disjunctive: element: Sequencing jobs on a single machine (b4seq2_ka.mos)
- element: element: Sequencing jobs on a single machine (b4seq_ka.mos), occurrence: Sugar production (a4sugar_ka.mos), equiv: Location of income tax offices (j5tax_ka.mos), implies: Paint production (b5paint_ka.mos), User-defined enumeration strategies (i1assign_ka.mos), 2D: implies: Paint production (b5paint2_ka.mos)
- distribute / occurrence: occurrence: Sugar production (a4sugar_ka.mos), distribute: Personnel planning (persplan.mos), equiv: Location of income tax offices (j5tax_ka.mos), Symmetry breaking: scenes allocation problem (scenesalloc.mos)
- maximum / minimum: Optimization and enumeration (i4exam3.mos, i4exam4.mos), element: Sequencing jobs on a single machine (b4seq2_ka.mos), abs and distance: Frequency assignment (freqasgn.mos), User-defined enumeration strategies (i1assign_ka.mos), Symmetry breaking: scenes allocation problem (scenesalloc.mos)
- implies / equiv: implies: Paint production (b5paint_ka.mos), distribute: Personnel planning (persplan.mos), equiv: Location of income tax offices (j5tax_ka.mos), Generic binary constraints: Euler knight tour (eulerkn2.mos), Symmetry breaking: scenes allocation problem (scenesalloc.mos)
- generic binary: Generic binary constraints: Euler knight tour (eulerkn.mos)
Constraint handling
In this section we shall work once more with the introductory problem of scheduling meetings from Section A first model. This model only contains simple arithmetic constraints over discrete variables. However, all that is said here equally applies to all other constraint types of Xpress Kalis, including constraint relations over continuous decision variables (that is, variables of the type cpfloatvar).
We now wish to state a few more constraints for this problem.
- Meeting B must take place before day 3.
- Meeting D cannot take place on day 2.
- Meeting A must be scheduled on day 1.
Model formulation
The three additional constraints translate into simple (unary) linear constraints. We complete our model as follows:
planB ≤ 2
planD ≠ 2
planA = 1
planA ≠ planB
planA ≠ planD
planB ≠ planC
planB ≠ planD
Implementation
The Mosel implementation of the new constraints is quite straightforward.
model "Meeting (2)"
uses "kalis"
declarations
MEETINGS = {'A','B','C','D'} ! Set of meetings
TIME = 1..3 ! Set of time slots
plan: array(MEETINGS) of cpvar ! Time slot per meeting
end-declarations
forall(m in MEETINGS) do
setdomain(plan(m), TIME)
setname(plan(m), "plan"+m)
end-do
writeln("Original domains: ", plan)
plan('B') <= 2 ! Meeting B before day 3
plan('D') <> 2 ! Meeting D not on day 2
plan('A') = 1 ! Meeting A on day 1
writeln("With constraints: ", plan)
! Respect incompatibilities
plan('A') <> plan('B')
plan('A') <> plan('D')
plan('B') <> plan('C')
plan('B') <> plan('D')
! Solve the problem
if not cp_find_next_sol then
writeln("Problem is infeasible")
exit(1)
end-if
! Solution printing
forall(m in MEETINGS)
writeln("Meeting ", m, ": ", getsol(plan(m)))
end-model
Results
As the reader may have noticed, we have added printout of the variables planm at several places in the model. The output generated by the execution of this model therefore is the following.
Original domains: [planA[1..3],planB[1..3],planC[1..3],planD[1..3]] With constraints: [planA[1],planB[1..2],planC[1..3],planD[1,3]] Meeting A: 1 Meeting B: 2 Meeting C: 1 Meeting D: 3
As can be seen from this output, immediately after stating the constraints, the domains of the concerned variables have been reduced. The constraints are immediately and automatically posted to the solver and their effects are propagated to the whole problem.
Naming constraints
Sometimes it may be necessary to access constraints later on, after their definition, in particular if they are to become part of logic relations or if they are to be branched on (typically the case for disjunctive constraints). To this aim kalis defines a new type, cpctr, that can be used to declare constraints giving them a name that can used after their definition. We define constraints by assigning to them a constraint relation.
Naming constraints has the secondary effect that the constraints are not automatically posted to the solver. This needs to be done by writing the name of a constraint as a statement on its own (after its definition) as shown in the following model.
model "Meeting (3)"
uses "kalis"
declarations
MEETINGS = {'A','B','C','D'} ! Set of meetings
TIME = 1..3 ! Set of time slots
plan: array(MEETINGS) of cpvar ! Time slot per meeting
Ctr: array(range) of cpctr
end-declarations
forall(m in MEETINGS) do
setdomain(plan(m), TIME)
setname(plan(m), "plan"+m)
end-do
writeln("Original domains: ", plan)
Ctr(1):= plan('B') <= 2 ! Meeting B before day 3
Ctr(2):= plan('D') <> 2 ! Meeting D not on day 2
Ctr(3):= plan('A') = 1 ! Meeting A on day 1
writeln("After definition of constraints:\n ", plan)
forall(i in 1..3) Ctr(i)
writeln("After posting of constraints:\n ", plan)
! Respect incompatibilities
plan('A') <> plan('B')
plan('A') <> plan('D')
plan('B') <> plan('C')
plan('B') <> plan('D')
! Solve the problem
if not cp_find_next_sol then
writeln("Problem is infeasible")
exit(1)
end-if
! Solution printing
forall(m in MEETINGS) writeln("Meeting ", m, ": ", getsol(plan(m)))
end-model
From the output produced by this model, we can see that the mere definition of named constraints does not have any effect on the domains of the variables (the constraints are defined in Mosel but not yet sent to the Kalis solver). Only after stating the names of the constraints (that is, sending them to the solver) we obtain the same domain reductions as with the previous version of the model.
Original domains: [planA[1..3],planB[1..3],planC[1..3],planD[1..3]] After definition of constraints: [planA[1..3],planB[1..3],planC[1..3],planD[1..3]] After posting of constraints: [planA[1],planB[1..2],planC[1..3],planD[1,3]] Meeting A: 1 Meeting B: 2 Meeting C: 1 Meeting D: 3
Explicit posting of constraints
In all previous examples, we have silently assumed that posting the constraints does not lead to a failure (infeasibility detected by the solver). In practice, this may not always be a reasonable assumption. kalis therefore defines the function cp_post that explicitly posts a constraint to the solver and returns the status of the constraint system after its addition (true for feasible and false for infeasible). This functionality may be of special interest for dealing with over-constrained problems to stop the addition of constraints once an infeasibility has been detected and to report back to the user which constraint has made the problem infeasible.
To use the explicit posting with cp_post, in the previous model we replace the line
forall(i in 1..3) Ctr(i)
with the following code.
forall(i in 1..3)
if not cp_post(Ctr(i)) then
writeln("Constraint ", i, " makes problem infeasible")
exit(1)
end-if
The return value of the every constraint posting is checked and the program is stopped if the addition of a constraint leads to an infeasibility.
The output produced by this model version is exactly the same as what we have seen in the previous section.
Explicit constraint propagation
The behavior of constraints can also be influenced in a different way. If we turn automated constraint propagation off,
setparam("KALIS_AUTO_PROPAGATE", false)
then constraints posted to the solver are not propagated. In this case, constraint propagation will only be launched by a call to cp_propagate or by starting the enumeration (subroutines cp_find_next_sol, cp_minimize, etc.).
Arithmetic constraints
In the previous sections we have already seen several examples of linear constraints over finite domain variables. Linear constraints may be regarded as a special case of arithmetic constraints, that is, equations or inequality relations involving expressions over decision variables formed with the operators +, -, /, *, ^, sum, prod and arithmetic functions like abs or ln. For a complete list of arithmetic functions supported by the solver the reader is refered to the Xpress Kalis Mosel Reference Manual.
Arithmetic constraints in Xpress Kalis may be defined over finite domain variables (type cpvar), continuous variables (type cpfloatvar), or mixtures of both. Notice, however, that arithmetic constraints involving continuous variables cannot be defined as strict inequalities, that means, only the relational operators >=, <=, and = may be used.
Here are a few examples of (nonlinear) arithmetic constraints that may be defined with Xpress Kalis in Mosel.
model "Nonlinear constraints"
uses "kalis"
setparam("KALIS_DEFAULT_LB", 0)
setparam("KALIS_DEFAULT_UB", 5)
setparam("KALIS_DEFAULT_CONTINUOUS_LB", -10)
setparam("KALIS_DEFAULT_CONTINUOUS_UB", 10)
declarations
a,b,c: cpvar
x,y,z: cpfloatvar
end-declarations
x = ln(y)
y = abs(z)
x*y <= z^2
z = -a/b
a*b*c^3 >= 150
while (cp_find_next_sol)
writeln("a:", getsol(a), ", b:", getsol(b), ", c:", getsol(c),
", x:", getsol(x), ", y:", getsol(y), ", z:", getsol(z))
end-model
all_different: Sudoku
Sudoku puzzles, originating from Japan, have recently made their appearance in many western newspapers. The idea of these puzzles is to complete a given, partially filled 9×9 board with the numbers 1 to 9 in such a way that no line, column, or 3×3 subsquare contains a number more than once. The tables Sudoku (`The Times', 26January, 2005) and Sudoku (`The Guardian', 29July, 2005) show two instances of such puzzles. Whilst sometimes tricky to solve for a human, these puzzles lend themselves to solving by a CP approach.
| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 3 | 6 | ||||||
| 2 | 6 | 5 | 7 | ||||||
| 3 | 8 | 7 | 3 | ||||||
| 4 | 5 | 1 | 3 | 7 | |||||
| 5 | 1 | 2 | 8 | 4 | |||||
| 6 | 9 | 7 | 5 | 2 | |||||
| 7 | 4 | 5 | 9 | ||||||
| 8 | 9 | 4 | 5 | ||||||
| 9 | 3 | 4 | 6 |
| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 3 | |||||||
| 2 | 5 | 4 | |||||||
| 3 | 2 | 7 | 6 | ||||||
| 4 | 1 | 5 | |||||||
| 5 | 3 | 9 | |||||||
| 6 | 6 | 4 | |||||||
| 7 | 7 | 2 | 3 | ||||||
| 8 | 4 | 1 | |||||||
| 9 | 9 | 8 |
Model formulation
As in the examples, we denote the columns of the board by the set XS = {A,B,...,I} and the rows by YS = {1,2,...,9}. For every x in XS and y in YS we define a decision variable vxy taking as its value the number at the position (x,y).
The only constraints in this problem are
(1) all numbers in a row must be different,
(2) all numbers in a column must be different,
(3) all numbers in a 3×3 subsquare must be different.
These constraints can be stated with Xpress Kalis's all_different relation. This constraint ensures that all variables in the relation take different values.
∀ x ∈ XS: all-different(vx1,...,vx9)
∀ y ∈ YS: all-different(vAy,...,vIy)
all-different(vA1,...,vC3)
all-different(vA4,...,vC6)
all-different(vA7,...,vC9)
all-different(vD1,...,vF3)
all-different(vD4,...,vF6)
all-different(vD7,...,vF9)
all-different(vG1,...,vI3)
all-different(vG4,...,vI6)
all-different(vG7,...,vI9)
In addition, certain variables vxy are fixed to the given values.
Implementation
The Mosel implementation for the Sudoku puzzle in Table Sudoku (`The Guardian', 29July, 2005) looks as follows.
model "sudoku (CP)"
uses "kalis"
forward procedure print_solution(numsol: integer)
setparam("kalis_default_lb", 1)
setparam("kalis_default_ub", 9) ! Default variable bounds
declarations
XS = {'A','B','C','D','E','F','G','H','I'} ! Columns
YS = 1..9 ! Rows
v: array(XS,YS) of cpvar ! Number assigned to cell (x,y)
end-declarations
! Data from "The Guardian", 29 July, 2005. http://www.guardian.co.uk/sudoku
v('A',1)=8; v('F',1)=3
v('B',2)=5; v('G',2)=4
v('A',3)=2; v('E',3)=7; v('H',3)=6
v('D',4)=1; v('I',4)=5
v('C',5)=3; v('G',5)=9
v('A',6)=6; v('F',6)=4
v('B',7)=7; v('E',7)=2; v('I',7)=3
v('C',8)=4; v('H',8)=1
v('D',9)=9; v('I',9)=8
! All-different values in rows
forall(y in YS) all_different(union(x in XS) {v(x,y)})
! All-different values in columns
forall(x in XS) all_different(union(y in YS) {v(x,y)})
! All-different values in 3x3 squares
forall(s in {{'A','B','C'},{'D','E','F'},{'G','H','I'}}, i in 0..2)
all_different(union(x in s, y in {1+3*i,2+3*i,3+3*i}) {v(x,y)})
! Solve the problem
solct:= 0
while (cp_find_next_sol) do
solct+=1
print_solution(solct)
end-do
writeln("Number of solutions: ", solct)
writeln("Time spent in enumeration: ",
getparam("KALIS_COMPUTATION_TIME"), "sec")
writeln("Number of nodes: ", getparam("KALIS_NODES"))
!****************************************************************
! Solution printing
procedure print_solution(numsol: integer)
writeln(getparam("KALIS_COMPUTATION_TIME"), "sec: Solution ", numsol)
writeln(" A B C D E F G H I")
forall(y in YS) do
write(y, ": ")
forall(x in XS)
write(getsol(v(x,y)), if(x in {'C','F'}, " | ", " "))
writeln
if y mod 3 = 0 then
writeln(" ---------------------")
end-if
end-do
end-procedure
end-model
In this model, the call to cp_find_next_sol is embedded in a while loop to search all feasible solutions. At every loop execution the procedure print_solution is called to print out the solution found nicely formatted. Subroutines in Mosel may have declarations blocks for local declarations and they may take any number of arguments. Since, in our model, the call to the procedure occurs before its definition, we need to declare it before the first call using the keyword forward.
For selecting the information that is to be printed by the subroutine we use two different versions of Mosel's if statement: the inline if and if-then that includes a block of statements.
At the end of the model run we retrieve from the solver the run time measurement (parameter KALIS_COMPUTATION_TIME) and the number of nodes explored by the search (parameter KALIS_NODES).
To obtain a complete list of parameters defined by the kalis module type the command
mosel exam -p kalis
(for a listing of the complete functionality of kalis leave out the flag -p).
Results
The model shown above generates the following output; this puzzle has only one solution, as is usually the case for Sudoku puzzles.
0.16sec: Solution 1 A B C D E F G H I 1: 8 6 9 | 2 4 3 | 1 5 7 2: 3 5 7 | 6 1 9 | 4 8 2 3: 2 4 1 | 8 7 5 | 3 6 9 --------------------- 4: 4 9 8 | 1 3 2 | 6 7 5 5: 7 1 3 | 5 8 6 | 9 2 4 6: 6 2 5 | 7 9 4 | 8 3 1 --------------------- 7: 1 7 6 | 4 2 8 | 5 9 3 8: 9 8 4 | 3 5 7 | 2 1 6 9: 5 3 2 | 9 6 1 | 7 4 8 --------------------- Number of solutions: 1 Time spent in enumeration: 0.41sec Number of nodes: 2712
The all_different relation takes an optional second argument that allows the user to specify the propagation algorithm to be used for evaluating the constraint. If we change from the default setting (KALIS_FORWARD_CHECKING) to the more aggressive strategy KALIS_GEN_ARC_CONSISTENCY by adding this choice as the second argument, for example,
forall(y in YS)
all_different(union(x in XS) {v(x,y)}, KALIS_GEN_ARC_CONSISTENCY)
we observe that the number of nodes is reduced to a single node—the problem is solved by simply posting the constraints. Whereas the time spent in the search is down to zero, the constraint posting now takes 4-5 times longer (still just a fraction of a second) due to the larger computational overhead of the generalized arc consistency algorithm. Allover, the time for problem definition and solving is reduced to less than a tenth of the previous time.
As a general rule, the generalized arc consistency algorithm achieves stronger pruning (i.e., it removes more values from the domains of the variables). However, due to the increase in computation time its use is not always justified. The reader is therefore encouraged to try both algorithm settings in his models.
abs and distance: Frequency assignment
The area of telecommunications, and in particular mobile telecommunications, gives rise to many different variants of frequency assignment problems.
We are given a network of cells (nodes) with requirements of discrete frequency bands. Each cell has a given demand for a number of frequencies (bands). Figure Telecommunications network shows the structure of the network. Nodes linked by an edge are considered as neighbors. They must not be assigned the same frequencies to avoid interference. Furthermore, if a cell uses several frequencies they must all be different by at least 2. The objective is to minimize the total number of frequencies used in the network.
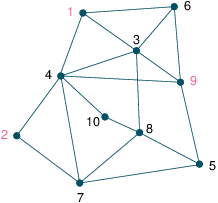
Figure 3.1: Telecommunications network
Table Frequency demands at nodes lists the number of frequency demands for every cell.
| Cell | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Demand | 4 | 5 | 2 | 3 | 2 | 4 | 3 | 4 | 3 | 2 |
Model formulation
Let NODES be the set of all nodes in the network and DEMn the demand of frequencies at node n ∈ NODES. The network is given as a set of edges LINKS. Furthermore, let DEMANDS = {1,2,...,NUMDEM} be the set of frequencies, numbered consecutively across all nodes where the upper bound NUMDEM is given by the total number of demands. The auxiliary array INDEXn indicates the starting index in DEMANDS for node n.
For representing the frequency assigned to every demand d ∈ DEMANDS we introduce the variables used that take their values from the set {1,2,...,NUMDEM}.
The two sets of constraints (different frequencies assigned to neighboring nodes and minimum distance between frequencies within a node) can then be modeled as follows.
| INDEXn+DEMn-1 |
| ⋃ |
| d=INDEXn |
| INDEXm+DEMm-1 |
| ⋃ |
| d=INDEXm |
∀ n ∈ NODES, ∀ c<d ∈ INDEXn,...,INDEXn+DEMn-1: |usec - used| ≥ 2
The objective function is to minimize to the number of frequencies used. We formulate this by minimizing the largest frequency number that occurs for the used variables:
Implementation
The edges forming the telecommunications network are modeled as a list LINK, where edge l is given as (LINK(l,1),LINK(l,2)).
For the implementation of the constraints on the values of frequencies assigned to the same node we have two equivalent choices with Kalis, namely using abs or distance constraints.
model "Frequency assignment"
uses "kalis"
forward procedure print_solution
declarations
NODES = 1..10 ! Range of nodes
LINKS = 1..18 ! Range of links between nodes
DEM: array(NODES) of integer ! Demand of nodes
LINK: array(LINKS,1..2) of integer ! Neighboring nodes
INDEX: array(NODES) of integer ! Start index in 'use'
NUMDEM: integer ! Upper bound on no. of freq.
end-declarations
DEM :: (1..10)[4, 5, 2, 3, 2, 4, 3, 4, 3, 2]
LINK:: (1..18,1..2)[1, 3, 1, 4, 1, 6,
2, 4, 2, 7,
3, 4, 3, 6, 3, 8, 3, 9,
4, 7, 4, 9, 4,10,
5, 7, 5, 8, 5, 9,
6, 9, 7, 8, 8,10]
NUMDEM:= sum(n in NODES) DEM(n)
! Correspondence of nodes and demand indices:
! use(d) d = 1, ..., DEM(1) correspond to the demands of node 1
! d = DEM(1)+1, ..., DEM(1)+DEM(2)) - " - node 2 etc.
INDEX(1):= 1
forall(n in NODES | n > 1) INDEX(n) := INDEX(n-1) + DEM(n-1)
declarations
DEMANDS = 1..NUMDEM ! Range of frequency demands
use: array(DEMANDS) of cpvar ! Frequency used for a demand
numfreq: cpvar ! Number of frequencies used
Strategy: array(range) of cpbranching
end-declarations
! Setting the domain of the decision variables
forall(d in DEMANDS) setdomain(use(d), 1, NUMDEM)
! All frequencies attached to a node must be different by at least 2
forall(n in NODES, c,d in INDEX(n)..INDEX(n)+DEM(n)-1 | c<d)
distance(use(c), use(d)) >= 2
! abs(use(c) - use(d)) >= 2
! Neighboring nodes take all-different frequencies
forall(l in LINKS)
all_different(
union(d in INDEX(LINK(l,1))..INDEX(LINK(l,1))+DEM(LINK(l,1))-1) {use(d)} +
union(d in INDEX(LINK(l,2))..INDEX(LINK(l,2))+DEM(LINK(l,2))-1) {use(d)},
KALIS_GEN_ARC_CONSISTENCY)
! Objective function: minimize the number of frequencies used, that is,
! minimize the largest value assigned to 'use'
setname(numfreq, "NumFreq")
numfreq = maximum(use)
! Search strategy
Strategy(1):=assign_var(KALIS_SMALLEST_DOMAIN, KALIS_MIN_TO_MAX, use)
Strategy(2):=assign_var(KALIS_MAX_DEGREE, KALIS_MIN_TO_MAX, use)
cp_set_branching(Strategy(1))
setparam("KALIS_MAX_COMPUTATION_TIME", 1)
cp_set_solution_callback(->print_solution)
! Try to find solution(s) with strategy 1
if cp_minimize(numfreq) then
cp_show_stats
sol:=getsol(numfreq)
end-if
! Restart search with strategy 2
cp_reset_search
if sol>0 then ! If a solution was found:
numfreq <= sol-1 ! Add upper bound on objective
end-if
cp_set_branching(Strategy(2))
setparam("KALIS_MAX_COMPUTATION_TIME", 1000)
if cp_minimize(numfreq) then
cp_show_stats
elif sol>0 then
writeln("Optimality proven")
else
writeln("Problem has no solution")
end-if
!********************************************************************
! **** Solution printout ****
procedure print_solution
writeln("Number of frequencies: ", getsol(numfreq))
writeln("Frequency assignment: ")
forall(n in NODES) do
write("Node ", n, ": ")
forall(d in INDEX(n)..INDEX(n)+DEM(n)-1) write(getsol(use(d)), " ")
writeln
end-do
end-procedure
end-model
With just the default search strategy this model finds a solution of value 11 but it runs for a long time without being able to prove optimality. When experimenting with different search strategies we have found that the strategy obtained by changing the variable selection criterion to KALIS_MAX_DEGREE is able to prove optimality easily once a good solution is known. This problem is therefore solved in two steps: First, we use the default strategy for finding a good solution. This search is stopped after one second by setting a time limit. The search is then restarted (previously, we needed to reset the search tree in the solver with cp_reset_search) with a second strategy and the bound on the objective value from the previous run.
To ease the experiments with different search strategies we have defined an array Strategy of type cpbranching that stores the different search strategy definitions.
Another new feature demonstrated by this implementation is the use of a callback, more precisely the solution callback of kalis. The solution callback is defined with a user subroutine that will be called by the solver whenever the search has found a solution. Its typical uses are logging or storing of intermediate solutions or performing some statistics. Our procedure print_solution simply prints out the solution that has been found.
Improving the problem formulation: we may observe that in our problem formulation all demand variables within a node and the constraints on these variables are entirely symmetric. In the absence of other constraints, we may reduce these symmetries by imposing an order on the use variables,
for demands d and d+1 belonging to the same cell. Doing so, the problem is solved to optimality within less than 40 nodes using just the default strategy. We may take this a step further by writing
The addition of these constraints shortens the search by yet a few more nodes. They can even be used simply in replacement of the abs or distance constraints.
Results
An optimal solution to this problem uses 11 different frequencies. The model shown in the program listing prints out the following assignment of frequencies to nodes:
Node 1: 1 3 5 7 Node 2: 1 3 5 7 10 Node 3: 2 8 Node 4: 4 6 9 Node 5: 4 6 Node 6: 4 6 9 11 Node 7: 2 8 11 Node 8: 1 3 5 7 Node 9: 1 3 5 Node 10: 2 8
element: Sequencing jobs on a single machine
The problem described in this section is taken from Section 7.4 `Sequencing jobs on a bottleneck machine' of the book `Applications of optimization with Xpress-MP'
The aim of this problem is to provide a model that may be used with different objective functions for scheduling operations on a single (bottleneck) machine. We shall see here how to minimize the total processing time, the average processing time, and the total tardiness.
A set of tasks (or jobs) is to be processed on a single machine. The execution of tasks is non-preemptive (that is, an operation may not be interrupted before its completion). For every task i its release date, duration, and due date are given in Table Task time windows and durations.
| Job | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Release date | 2 | 5 | 4 | 0 | 0 | 8 | 9 |
| Duration | 5 | 6 | 8 | 4 | 2 | 4 | 2 |
| Due date | 10 | 21 | 15 | 10 | 5 | 15 | 22 |
What is the optimal value for each of the objectives: minimizing the total duration of the schedule (makespan), the mean processing time or the total tardiness (that is, the amount of time by which the completion of jobs exceeds their respective due dates)?
Model formulation 1
We are going to present two alternative model formulations. The first is closer to the Mathematical Programming formulation in `Applications of optimization with Xpress-MP'. The second uses disjunctive constraints and branching on these. In both model formulations we are going deal with the different objective functions in sequence, but the body of the models will remain the same.
To represent the sequence of jobs we introduce variables rankk (k ∈ JOBS = {1,...,NJ}) that take as value the number of the job in position (rank) k. Every job j takes a single position. This constraint can be represented by an all-different on the rankk variables:
The processing time durk for the job in position k is given by DURrankk (where DUR_j denotes the duration given in the table in the previous section). Similarly, the release time relk is given by RELrankk (where REL_j denotes the given release date):
∀ k ∈ JOBS: relk = RELrankk
If startk is the start time of the job at position k, this value must be at least as great as the release date of the job assigned to this position. The completion time compk of this job is the sum of its start time plus its duration:
∀ k ∈ JOBS: compk = startk + durk
Another constraint is needed to specify that two jobs cannot be processed simultaneously. The job in position k+1 must start after the job in position k has finished, hence the following constraints:
Objective 1: The first objective is to minimize the makespan (completion time of the schedule), or, equivalently, to minimize the completion time of the last job (job with rank NJ). The complete model is then given by the following (where MAXTIME is a sufficiently large value, such as the sum of all release dates and all durations):
∀ k ∈ JOBS: rankk ∈ JOBS
∀ k ∈ JOBS: startk,compk ∈ {0,...,MAXTIME}
∀ k ∈ JOBS: durk ∈ {minj ∈ JOBS DURj,...,maxj ∈ JOBS DURj}
∀ k ∈ JOBS: relk ∈ {minj ∈ JOBS RELj,...,maxj ∈ JOBS RELj}
all-different(rank1,...,rankNJ)
∀ k ∈ JOBS: durk = DURrankk
∀ k ∈ JOBS: relk = RELrankk
∀ k ∈ JOBS: startk ≥ relk
∀ k ∈ JOBS: compk = startk + durk
∀ k ∈ {1,...,NJ-1}: startk+1 ≥ startk + durk
Objective 2: For minimizing the average processing time, we introduce an additional variable totComp representing the sum of the completion times of all jobs. We add the following constraint to the problem to calculate totComp:
| ∑ |
| k ∈ JOBS |
The new objective consists of minimizing the average processing time, or equivalently, minimizing the sum of the job completion times:
Objective 3: If we now aim to minimize the total tardiness, we again introduce new variables—this time to measure the amount of time that jobs finish after their due date. We write latek for the variable that corresponds to the tardiness of the job with rank k. Its value is the difference between the completion time of a job j and its due date DUEj. If the job finishes before its due date, the value must be zero. We thus obtain the following constraints:
∀ k ∈ JOBS: latek ≥ compk - duek
For the formulation of the new objective function we introduce the variable totLate representing the total tardiness of all jobs. The objective now is to minimize the value of this variable:
totLate =
| ∑ |
| k ∈ JOBS |
Implementation of model 1
The Mosel implementation below solves the same problem three times, each time with a different objective, and prints the resulting solutions by calling the procedures print_sol and print_sol3.
model "B-4 Sequencing (CP)"
uses "kalis"
forward procedure print_sol
forward procedure print_sol3
declarations
NJ = 7 ! Number of jobs
JOBS=1..NJ
REL: array(JOBS) of integer ! Release dates of jobs
DUR: array(JOBS) of integer ! Durations of jobs
DUE: array(JOBS) of integer ! Due dates of jobs
rank: array(JOBS) of cpvar ! Number of job at position k
start: array(JOBS) of cpvar ! Start time of job at position k
dur: array(JOBS) of cpvar ! Duration of job at position k
comp: array(JOBS) of cpvar ! Completion time of job at position k
rel: array(JOBS) of cpvar ! Release date of job at position k
end-declarations
initializations from 'Data/b4seq.dat'
DUR REL DUE
end-initializations
MAXTIME:= max(j in JOBS) REL(j) + sum(j in JOBS) DUR(j)
MINDUR:= min(j in JOBS) DUR(j); MAXDUR:= max(j in JOBS) DUR(j)
MINREL:= min(j in JOBS) REL(j); MAXREL:= max(j in JOBS) REL(j)
forall(j in JOBS) do
1 <= rank(j); rank(j) <= NJ
0 <= start(j); start(j) <= MAXTIME
MINDUR <= dur(j); dur(j) <= MAXDUR
0 <= comp(j); comp(j) <= MAXTIME
MINREL <= rel(j); rel(j) <= MAXREL
end-do
! One posistion per job
all_different(rank)
! Duration of job at position k
forall(k in JOBS) dur(k) = element(DUR, rank(k))
! Release date of job at position k
forall(k in JOBS) rel(k) = element(REL, rank(k))
! Sequence of jobs
forall(k in 1..NJ-1) start(k+1) >= start(k) + dur(k)
! Start times
forall(k in JOBS) start(k) >= rel(k)
! Completion times
forall(k in JOBS) comp(k) = start(k) + dur(k)
! Set the branching strategy
cp_set_branching(split_domain(KALIS_SMALLEST_DOMAIN, KALIS_MIN_TO_MAX))
!**** Objective function 1: minimize latest completion time ****
if cp_minimize(comp(NJ)) then
print_sol
end-if
!**** Objective function 2: minimize average completion time ****
declarations
totComp: cpvar
end-declarations
totComp = sum(k in JOBS) comp(k)
if cp_minimize(totComp) then
print_sol
end-if
!**** Objective function 3: minimize total tardiness ****
declarations
late: array(JOBS) of cpvar ! Lateness of job at position k
due: array(JOBS) of cpvar ! Due date of job at position k
totLate: cpvar
end-declarations
MINDUE:= min(k in JOBS) DUE(k); MAXDUE:= max(k in JOBS) DUE(k)
forall(k in JOBS) do
MINDUE <= due(k); due(k) <= MAXDUE
0 <= late(k); late(k) <= MAXTIME
end-do
! Due date of job at position k
forall(k in JOBS) due(k) = element(DUE, rank(k))
! Late jobs: completion time exceeds the due date
forall(k in JOBS) late(k) >= comp(k) - due(k)
totLate = sum(k in JOBS) late(k)
if cp_minimize(totLate) then
writeln("Tardiness: ", getsol(totLate))
print_sol
print_sol3
end-if
!-----------------------------------------------------------------
! Solution printing
procedure print_sol
writeln("Completion time: ", getsol(comp(NJ)) ,
" average: ", getsol(sum(k in JOBS) comp(k)))
write("\t")
forall(k in JOBS) write(strfmt(getsol(rank(k)),4))
write("\nRel\t")
forall(k in JOBS) write(strfmt(getsol(rel(k)),4))
write("\nDur\t")
forall(k in JOBS) write(strfmt(getsol(dur(k)),4))
write("\nStart\t")
forall(k in JOBS) write(strfmt(getsol(start(k)),4))
write("\nEnd\t")
forall(k in JOBS) write(strfmt(getsol(comp(k)),4))
writeln
end-procedure
procedure print_sol3
write("Due\t")
forall(k in JOBS) write(strfmt(getsol(due(k)),4))
write("\nLate\t")
forall(k in JOBS) write(strfmt(getsol(late(k)),4))
writeln
end-procedure
end-model
NB: The reader may have been wondering why we did not use the more obvious pair start-end for naming the variables in this example: end is a keyword of the Mosel language (see the list of reserved words in the Mosel Language Reference Manual), which means that neither end nor END may be redefined by a Mosel program. It is possible though, to use versions combining lower and upper case letters, like End, but to prevent any possible confusion we do not recommend their use.
Results
The minimum makespan of the schedule is 31, the minimum sum of completion times is 103 (which gives an average of 103/7=14.71). A schedule with this objective value is 5→ 4→ 1→ 7→ 6→ 2→ 3. If we compare the completion times with the due dates we see that jobs 1, 2, 3, and 6 finish late (with a total tardiness of 21). The minimum tardiness is 18. A schedule with this tardiness is 5→ 1→ 4→ 6→ 2→ 7→ 3 where jobs 4 and 7 finish one time unit late and job 3 is late by 16 time units, and it terminates at time 31 instead of being ready at its due date, time 15. This schedule has an average completion time of 15.71.
Alternative formulation using disjunctions
Our second model formulation is possibly a more straightforward way of representing the problem. It introduces disjunctive constraints and branching on these.
Every job is now represented by its starting time, variables startj (j ∈ JOBS = {1,...,NJ}) that take their values in {RELj,...,MAXTIME} (where MAXTIME is a sufficiently large value, such as the sum of all release dates and all durations, and RELj the release date of job j). We state the disjunctions as a single disjunctive relation on the start times and durations of all jobs.
This constraint replaces the pair-wise disjunctions
for all pairs of jobs i < j ∈ JOBS.
The processing time durk for the job in position k is given by DURrankk (where DUR_j denotes the duration given in the table in the previous section). Similarly, its release time relk is given by RELrankk (where REL_j denotes the given release date).
∀ k ∈ JOBS: relk = RELrankk
The completion time compj of a job j is the sum of its start time plus its duration DURj.
Objective 1: The first objective is to minimize the makespan (completion time of the schedule) or, equivalently, to minimize the completion time finish of the last job. The complete model is then given by the following (where MAXTIME is a sufficiently large value, such as the sum of all release dates and all durations):
finish = maximumj ∈ JOBS(compj)
∀ j ∈ JOBS: compj ∈ {0,...,MAXTIME}
∀ j ∈ JOBS: startj ∈ {RELj,...,MAXTIME}
disjunctive([start1,...,startNJ], [DUR1,...,DURNJ])
∀ j ∈ JOBS: compj = startj + DURj
Objective 2: The formulation of the second objective (minimizing the average processing time or, equivalently, minimizing the sum of the job completion times) remains unchanged from the first model—we introduce an additional variable totComp representing the sum of the completion times of all jobs.
totComp =
| ∑ |
| k ∈ JOBS |
Objective 3: To formulate the objective of minimizing the total tardiness, we introduce new variables latej to measure the amount of time that a job finishes after its due date. The value of these variables corresponds to the difference between the completion time of a job j and its due date DUEj. If the job finishes before its due date, the value must be zero. The objective now is to minimize the sum of these tardiness variables:
totLate =
| ∑ |
| j ∈ JOBS |
∀ j ∈ JOBS: latej ∈ {0,...,MAXTIME}
∀ j ∈ JOBS: latej ≥ compj - DUEj
Implementation of model 2
As with model 1, the Mosel implementation below solves the same problem three times, each time with a different objective, and prints the resulting solutions by calling the procedures print_sol and print_sol3.
model "B-4 Sequencing (CP)"
uses "kalis"
forward procedure print_sol
forward procedure print_sol3
declarations
NJ = 7 ! Number of jobs
JOBS=1..NJ
REL: array(JOBS) of integer ! Release dates of jobs
DUR: array(JOBS) of integer ! Durations of jobs
DUE: array(JOBS) of integer ! Due dates of jobs
DURS: array(set of cpvar) of integer ! Dur.s indexed by start variables
start: array(JOBS) of cpvar ! Start time of jobs
comp: array(JOBS) of cpvar ! Completion time of jobs
finish: cpvar ! Completion time of the entire schedule
Disj: set of cpctr ! Disjunction constraints
Strategy: array(range) of cpbranching ! Branching strategy
end-declarations
initializations from 'Data/b4seq.dat'
DUR REL DUE
end-initializations
MAXTIME:= max(j in JOBS) REL(j) + sum(j in JOBS) DUR(j)
forall(j in JOBS) do
0 <= start(j); start(j) <= MAXTIME
0 <= comp(j); comp(j) <= MAXTIME
end-do
! Disjunctions between jobs
forall(j in JOBS) DURS(start(j)):= DUR(j)
disjunctive(union(j in JOBS) {start(j)}, DURS, Disj, 1)
! Start times
forall(j in JOBS) start(j) >= REL(j)
! Completion times
forall(j in JOBS) comp(j) = start(j) + DUR(j)
!**** Objective function 1: minimize latest completion time ****
finish = maximum(comp)
Strategy(1):= settle_disjunction(Disj)
Strategy(2):= split_domain(KALIS_LARGEST_MAX, KALIS_MIN_TO_MAX)
cp_set_branching(Strategy)
if cp_minimize(finish) then
print_sol
end-if
!**** Objective function 2: minimize average completion time ****
declarations
totComp: cpvar
end-declarations
totComp = sum(k in JOBS) comp(k)
if cp_minimize(totComp) then
print_sol
end-if
!**** Objective function 3: minimize total tardiness ****
declarations
late: array(JOBS) of cpvar ! Lateness of jobs
totLate: cpvar
end-declarations
forall(k in JOBS) do
0 <= late(k); late(k) <= MAXTIME
end-do
! Late jobs: completion time exceeds the due date
forall(j in JOBS) late(j) >= comp(j) - DUE(j)
totLate = sum(k in JOBS) late(k)
if cp_minimize(totLate) then
writeln("Tardiness: ", getsol(totLate))
print_sol
print_sol3
end-if
!-----------------------------------------------------------------
! Solution printing
procedure print_sol
writeln("Completion time: ", getsol(finish) ,
" average: ", getsol(sum(j in JOBS) comp(j)))
write("Rel\t")
forall(j in JOBS) write(strfmt(REL(j),4))
write("\nDur\t")
forall(j in JOBS) write(strfmt(DUR(j),4))
write("\nStart\t")
forall(j in JOBS) write(strfmt(getsol(start(j)),4))
write("\nEnd\t")
forall(j in JOBS) write(strfmt(getsol(comp(j)),4))
writeln
end-procedure
procedure print_sol3
write("Due\t")
forall(j in JOBS) write(strfmt(DUE(j),4))
write("\nLate\t")
forall(j in JOBS) write(strfmt(getsol(late(j)),4))
writeln
end-procedure
end-model
This implementation introduces a new branching scheme, namely settle_disjunction. As opposed to the branching strategies we have seen so far this scheme defines a branching strategy over constraints, and not over variables. With this scheme a node is created by choosing a constraint from the given set and the branches from the node are obtained by adding one of the mutually exclusive constraints forming this disjunctive constraint to the constraint system.
NB: the disjunctive constraint of Xpress Kalis establishes pair-wise inequalities between the processing times of tasks. However, the definition of disjunctive constraints is not restricted to this case: a disjunction may have more than two components, and involve constraints of any type, including other logic relations obtained by combining constraints with and or or.
occurrence: Sugar production
The problem description in this section is taken from Section 6.4 `Cane sugar production' of the book `Applications of optimization with Xpress-MP'
The harvest of cane sugar in Australia is highly mechanized. The sugar cane is immediately transported to a sugarhouse in wagons that run on a network of small rail tracks. The sugar content of a wagonload depends on the field it has been harvested from and on the maturity of the sugar cane. Once harvested, the sugar content decreases rapidly through fermentation and the wagonload will entirely lose its value after a certain time. At this moment, eleven wagons loaded with the same quantity have arrived at the sugarhouse. They have been examined to find out the hourly loss and the remaining life span (in hours) of every wagon, these data are summarized in the following table.
| Lot | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Loss (kg/h) | 43 | 26 | 37 | 28 | 13 | 54 | 62 | 49 | 19 | 28 | 30 |
| Life span (h) | 8 | 8 | 2 | 8 | 4 | 8 | 8 | 8 | 8 | 8 | 8 |
Every lot may be processed by any of the three, fully equivalent production lines of the sugarhouse. The processing of a lot takes two hours. It must be finished at the latest at the end of the life span of the wagonload. The manager of the sugarhouse wishes to determine a production schedule for the currently available lots that minimizes the total loss of sugar.
Model formulation
Let WAGONS = {1,...,NW} be the set of wagons, NL the number of production lines and DUR the duration of the production process for every lot. The hourly loss for every wagon w is given by LOSSw and its life span by LIFEw. We observe that, in an optimal solution, the production lines need to work without any break—otherwise we could reduce the loss in sugar by advancing the start of the lot that follows the break. This means that the completion time of every lot is of the form s · DUR, with s > 0 and is an integer. The maximum value of s is the number of time slots (of length DUR) that the sugarhouse will work, namely NS = ceil(NW/NL), where ceil stands for `rounded to the next largest integer'. If NW/NL is an integer, every line will process exactly NS lots. Otherwise, some lines will process NS-1 lots, but at least one line processes NS lots. In all cases, the length of the optimal schedule is NS · DUR hours. We call SLOTS = {1,...,NS} the set of time slots.
Every lot needs to be assigned to a time slot. We define variables processw for the time slot assigned to wagon w and variables lossw for the loss incurred by this wagonload. Every time slot may take up to NL lots because there are NL parallel lines; therefore, we limit the number of occurrences of time slot values among the processw variables (this constraint relation is often called cardinality constraint):
The loss of sugar per wagonload w and time slot s is COSTws = s · DUR · LOSSw. Let variables lossw denote the loss incurred by wagon load w:
The objective function (total loss of sugar) is then given as the sum of all losses:
| ∑ |
| w ∈ WAGONS |
Implementation
The following model is the Mosel implementation of this problem. It uses the function ceil to calculate the maximum number of time slots.
The constraints on the processing variables are expressed by occurrence relations and the losses are obtained via element constraints. The branching strategy uses the variable selection criterion KALIS_SMALLEST_MAX, that is, choosing the variable with the smallest upper bound.
model "A-4 Cane sugar production (CP)"
uses "kalis", "mmsystem"
declarations
NW = 11 ! Number of wagon loads of sugar
NL = 3 ! Number of production lines
WAGONS = 1..NW
NS = ceil(NW/NL)
SLOTS = 1..NS ! Time slots for production
LOSS: array(WAGONS) of integer ! Loss in kg/hour
LIFE: array(WAGONS) of integer ! Remaining time per lot (in hours)
DUR: integer ! Duration of the production (in hours)
COST: array(SLOTS) of integer ! Cost per wagon
loss: array(WAGONS) of cpvar ! Loss per wagon
process: array(WAGONS) of cpvar ! Time slots for wagon loads
totalLoss: cpvar ! Objective variable
end-declarations
initializations from 'Data/a4sugar.dat'
LOSS LIFE DUR
end-initializations
forall(w in WAGONS) setdomain(process(w), 1, NS)
! Wagon loads per time slot
forall(s in SLOTS) occurrence(s, process) <= NL
! Limit on raw product life
forall(w in WAGONS) process(w) <= floor(LIFE(w)/DUR)
! Objective function: total loss
forall(w in WAGONS) do
forall(s in SLOTS) COST(s):= s*DUR*LOSS(w)
loss(w) = element(COST, process(w))
end-do
totalLoss = sum(w in WAGONS) loss(w)
cp_set_branching(assign_var(KALIS_SMALLEST_MAX, KALIS_MIN_TO_MAX, process))
! Solve the problem
if not cp_minimize(totalLoss) then
writeln("No solution found")
exit(0)
end-if
! Solution printing
writeln("Total loss: ", getsol(totalLoss))
forall(s in SLOTS) do
write("Slot ", s, ": ")
forall(w in WAGONS | getsol(process(w))=s)
write(formattext("wagon %2d (%3g) ", w, s*DUR*LOSS(w)))
writeln
end-do
end-model
An alternative formulation of the constraints on the processing variables is to replace them by a single distribute relation, indicating for every time slot the minimum and maximum number (MINUSEs=0 and MAXUSEs=NL) of production lines that may be used.
forall(s in SLOTS) MAXUSE(s):= NL distribute(process, SLOTS, MINUSE, MAXUSE)
Yet another formulation of this problem is possible with Xpress Kalis, namely interpreting it as a cumulative scheduling problem (see Section Cumulative scheduling: discrete resources), where the wagon loads are represented by tasks of unit duration, scheduled on a discrete resource with a capacity corresponding to the number of production lines.
Results
We obtain a total loss of 1620 kg of sugar. The corresponding schedule of lots is shown in the following Table Optimal schedule for the cane sugar lots (there are several equivalent solutions).
| Slot 1 | Slot 2 | Slot 3 | Slot 4 |
|---|---|---|---|
| lot 3 (74 kg) | lot 1 (172 kg) | lot 4 (168 kg) | lot 2 (208 kg) |
| lot 6 (108 kg) | lot 5 (52 kg) | lot 9 (114 kg) | lot 10 (224 kg) |
| lot 7 (124 kg) | lot 8 (196 kg) | lot 11 (180 kg) |
distribute: Personnel planning
The director of a movie theater wishes to establish a plan with the working locations for his personnel. The theater has eight employees: David, Andrew, Leslie, Jason, Oliver, Michael, Jane, and Marilyn. The ticket office needs to be staffed with three persons, theater entrances one and two require two persons each, and one person needs to be put in charge of the cloakroom. Due to different qualifications and respecting individual likes and dislikes, the following constraints need to be taken into account:
- Leslie must be at the second entrance of the theater.
- Michael must be at the first entrance of the theater.
- David, Michael and Jason cannot work with each other.
- If Oliver is selling tickets, Marylin must be with him.
Model formulation
Let PERS be the set of personnel and LOC = {1,...,4} the set of working locations where 1 stands for the ticket office, 2 and 3 for entrances 1 and 2 respectively, and 4 for the cloakroom.
We introduce decision variables placep for the working location assigned to person p. The four individual constraints on working locations can then be stated as follows:
placeMichael = 2
all-different(placeDavid,placeMichael,placeJason)
placeOliver = 1 ⇒ placeMarylin = 1
We also have to meet the staffing requirement of every working location:
Implementation
For the implementation of the staffing requirements we may choose among two different constraints of Xpress Kalis, namely occurrence constraints (one per working location) or a distribute constraint (also known as global cardinality constraint) over all working locations. The following model shows both options. As opposed to the previous example (Section Implementation we now have equality constraints. We therefore use the three-argument version of distribute (instead of the version with four arguments where the last two are the lower and upper bounds respectively).
For an attractive display, the model also introduces a few auxiliary data structures with the names of the working locations and the corresponding index values in the set LOC.
model "Personnel Planning (CP)"
uses "kalis"
forward procedure print_solution
declarations
PERS = {"David","Andrew","Leslie","Jason","Oliver","Michael",
"Jane","Marilyn"} ! Set of personnel
LOC = 1..4 ! Set of locations
LOCNAMES = {"Ticketoffice", "Theater1", "Theater2",
"Cloakroom"} ! Names of locations
LOCNUM: array(LOCNAMES) of integer ! Numbers assoc. with loc.s
REQ: array(LOC) of integer ! No. of pers. req. per loc.
place: array(PERS) of cpvar ! Workplace assigned to each peson
end-declarations
! Initialize data
LOCNUM("Ticketoffice"):= 1; LOCNUM("Theater1"):= 2
LOCNUM("Theater2"):= 3; LOCNUM("Cloakroom"):= 4
REQ:: (1..4)[3, 2, 2, 1]
! Each variable has a lower bound of 1 (Ticketoffice) and an upper bound
! of 4 (Cloakroom)
forall(p in PERS) do
setname(place(p),"workplace["+p+"]")
setdomain(place(p), LOC)
end-do
! "Leslie must be at the second entrance of the theater"
place("Leslie") = LOCNUM("Theater2")
! "Michael must be at the first entrance of the theater"
place("Michael") = LOCNUM("Theater1")
! "David, Michael and Jason cannot work with each other"
all_different({place("David"), place("Michael"), place("Jason")})
! "If Oliver is selling tickets, Marylin must be with him"
implies(place("Oliver")=LOCNUM("Ticketoffice"),
place("Marilyn")=LOCNUM("Ticketoffice"))
! Creation of a resource constraint of for every location
! forall(d in LOC) occurrence(LOCNUM(d), place) = REQ(d)
! Formulation of resource constraints using global cardinality constraint
distribute(place, LOC, REQ)
! Setting parameters of the enumeration
cp_set_branching(assign_var(KALIS_SMALLEST_MIN, KALIS_MAX_TO_MIN, place))
! Solve the problem
if not cp_find_next_sol then
writeln("Problem is infeasible")
exit(1)
end-if
! Solution output
nbSolutions:= 1
print_solution
! Search for other solutions
while (cp_find_next_sol) do
nbSolutions += 1
print_solution
end-do
! **** Solution printout ****
procedure print_solution
declarations
LOCIDX: array(LOC) of string
end-declarations
forall(l in LOCNAMES) LOCIDX(LOCNUM(l)):=l
writeln("\nSolution number ", nbSolutions)
forall(p in PERS)
writeln(" Working place of ", p, ": ", LOCIDX(getsol(place(p))))
end-procedure
end-model
Since we merely wish to find a feasible assignment of working locations, this model first tests whether a feasible solution exists. If this is the case, it also enumerates all other feasible solutions. Each time a solution is found it is printed out by call to the procedure print_solution.
Results
This problem has 38 feasible solutions. A graphical representation of a feasible assignment is shown in Figure Personnel schedule representation.
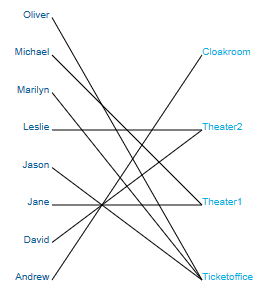
Figure 3.2: Personnel schedule representation
The following Mosel code was used for generating the graphic (see the documentation of module mmsvg in the Mosel Language Reference Manual for further explanation).
! **** Solution printout and graphical display ****
procedure draw_solution
svgerase
svgaddgroup("PersGraph", "Personnel")
svgsetstyle(SVG_TEXTANCHOR, "end")
svgaddgroup("LocGraph", "Locations")
svgaddgroup("AsgnGraph", "Assignments", SVG_BLACK)
forall(d in LOCNAMES)
svgaddtext("LocGraph", 4, LOCNUM(d), d)
FACT:=LOCNAMES.size/PERS.size
idx:= 1
forall(p in PERS, idx as counter) do
svgaddline("AsgnGraph", 2, idx*FACT, 4, getsol(place(p)))
svgaddtext("PersGraph", 2, idx*FACT, p)
end-do
svgsetgraphscale(75)
svgsetgraphviewbox(0,0,5,LOCNAMES.size+1)
svgrefresh
! Uncomment to pause at every iteration:
if nbSolutions<MAXSOL then svgpause; end-if
end-procedure
implies: Paint production
The problem description in this section is taken from Section 7.5 `Paint production' of the book `Applications of optimization with Xpress-MP'
As a part of its weekly production a paint company produces five batches of paints, always the same, for some big clients who have a stable demand. Every paint batch is produced in a single production process, all in the same blender that needs to be cleaned between every two batches. The durations of blending paint batches 1 to 5 are respectively 40, 35, 45, 32, and 50 minutes. The cleaning times depend on the colors and the paint types. For example, a long cleaning period is required if an oil-based paint is produced after a water-based paint, or to produce white paint after a dark color. The times are given in minutes in the following Table Matrix of cleaning times CLEAN where CLEANij denotes the cleaning time between batch i and batch j.
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 11 | 7 | 13 | 11 |
| 2 | 5 | 0 | 13 | 15 | 15 |
| 3 | 13 | 15 | 0 | 23 | 11 |
| 4 | 9 | 13 | 5 | 0 | 3 |
| 5 | 3 | 7 | 7 | 7 | 0 |
Since the company also has other activities, it wishes to deal with this weekly production in the shortest possible time (blending and cleaning). Which is the corresponding order of paint batches? The order will be applied every week, so the cleaning time between the last batch of one week and the first of the following week needs to be counted for the total duration of cleaning.
Formulation of model 1
As for the problem in Section element: Sequencing jobs on a single machine we are going to present two alternative model formulations. The first one is closer to the Mathematical Programming formulation in `Applications of optimization with Xpress-MP', the second uses a two-dimensional element constraint.
Let JOBS = {1,...,NJ} be the set of batches to produce, DURj the processing time for batch j, and CLEANij the cleaning time between the consecutive batches i and j. We introduce decision variables succj taking their values in JOBS, to indicate the successor of every job, and variables cleanj for the duration of the cleaning after every job. The cleaning time after every job is obtained by indexing CLEANij with the value of succj. We thus have the following problem formulation.
| ∑ |
| j ∈ JOBS |
∀ j ∈ JOBS: succj ∈ JOBS \ {j}
∀ j ∈ JOBS: cleanj = CLEANj,succj
all-different(
| ⋃ |
| j ∈ JOBS |
The objective function sums up the processing and cleaning times of all batches. The last (all-different) constraint guarantees that every batch occurs exactly once in the production sequence.
Unfortunately, this model does not guarantee that the solution forms a single cycle. Solving it indeed results in a total duration of 239 with an invalid solution that contains two sub-cycles 1 → 3 → 2 → 1 and 4 → 5 → 4. A first possibility is to add a disjunction excluding this solution to our model and re-solve it iteratively until we reach a solution without sub-cycles.
However, this procedure is likely to become impractical with larger data sets since it may potentially introduce an extremely large number of disjunctions. We therefore choose a different, a-priori formulation of the sub-cycle elimination constraints with a variable yj per batch and NJ · (NJ-1) implication constraints.
∀ i ∈ JOBS, ∀ j = 2,...,NJ, i ≠ j : succi = j ⇒ yj = yi + 1
The variables yj correspond to the position of job j in the production cycle. With these constraints, job 1 always takes the first position.
Implementation of model 1
The Mosel implementation of the model formulated in the previous section is quite straightforward. The sub-cycle elimination constraints are implemented as logic relations with implies (a stronger formulation of these constraints is obtained by replacing the implications by equivalences, using equiv).
model "B-5 Paint production (CP)"
uses "kalis", "mmsystem"
declarations
NJ = 5 ! Number of paint batches (=jobs)
JOBS=1..NJ
DUR: array(JOBS) of integer ! Durations of jobs
CLEAN: array(JOBS,JOBS) of integer ! Cleaning times between jobs
CB: array(JOBS) of integer ! Cleaning times after a batch
succ: array(JOBS) of cpvar ! Successor of a batch
clean: array(JOBS) of cpvar ! Cleaning time after batches
y: array(JOBS) of cpvar ! Variables for excluding subtours
cycleTime: cpvar ! Objective variable
end-declarations
initializations from 'Data/b5paint.dat'
DUR CLEAN
end-initializations
forall(j in JOBS) do
1 <= succ(j); succ(j) <= NJ; succ(j) <> j
1 <= y(j); y(j) <= NJ
end-do
! Cleaning time after every batch
forall(j in JOBS) do
forall(i in JOBS) CB(i):= CLEAN(j,i)
clean(j) = element(CB, succ(j))
end-do
! Objective: minimize the duration of a production cycle
cycleTime = sum(j in JOBS) (DUR(j)+clean(j))
! One successor and one predecessor per batch
all_different(succ)
! Exclude subtours
forall(i in JOBS, j in 2..NJ | i<>j)
implies(succ(i) = j, y(j) = y(i) + 1)
! Solve the problem
if not cp_minimize(cycleTime) then
writeln("Problem is infeasible")
exit(1)
end-if
cp_show_stats
! Solution printing
writeln("Minimum cycle time: ", getsol(cycleTime))
writeln("Sequence of batches:\nBatch Duration Cleaning")
first:=1
repeat
writeln(formattext(" %d%8d%9d", first, DUR(first), clean(first).sol))
first:=getsol(succ(first))
until (first=1)
end-model
Formulation of model 2
We may choose to implement the paint production problem using rank variables similarly to the sequencing model in Section Model formulation 1.
As before, let JOBS = {1,...,NJ} be the set of batches to produce, DURj the processing time for batch j, and CLEANij the cleaning time between the consecutive batches i and j. We introduce decision variables rankk taking their values in JOBS, for the number of the job in position k. Variables cleank (k ∈ JOBS) now denote the duration of the kth cleaning time. This duration is obtained by indexing CLEANij with the values of two consecutive rankk variables. We thus have the following problem formulation.
| ∑ |
| j ∈ JOBS |
| ∑ |
| k ∈ JOBS |
∀ k ∈ JOBS: rankk ∈ JOBS
∀ k ∈ {1,...,NJ-1}: cleank = CLEANrankk,rankk+1
cleanNJ = CLEANrankNJ,rank1
all-different(
| ⋃ |
| k ∈ JOBS |
As in model 1, the objective function sums up the processing and cleaning times of all batches. Although not strictly necessary from the mathematical point of view, we use different sum indices for durations and cleaning times to show the difference between summing over jobs or job positions. We now have an all-different constraint over the rank variables to guarantee that every batch occurs exactly once in the production sequence.
Implementation of model 2
The implementation of the second model uses the 2-dimensional version of the element constraint in Xpress Kalis.
model "B-5 Paint production (CP)"
uses "kalis", "mmsystem"
declarations
NJ = 5 ! Number of paint batches (=jobs)
JOBS=1..NJ
DUR: array(JOBS) of integer ! Durations of jobs
CLEAN: array(JOBS,JOBS) of integer ! Cleaning times between jobs
rank: array(JOBS) of cpvar ! Number of job in position k
clean: array(JOBS) of cpvar ! Cleaning time after batches
cycleTime: cpvar ! Objective variable
end-declarations
initializations from 'Data/b5paint.dat'
DUR CLEAN
end-initializations
forall(k in JOBS) setdomain(rank(k), JOBS)
! Cleaning time after every batch
forall(k in JOBS)
if k<NJ then
element(CLEAN, rank(k), rank(k+1)) = clean(k)
else
element(CLEAN, rank(k), rank(1)) = clean(k)
end-if
! Objective: minimize the duration of a production cycle
cycleTime = sum(j in JOBS) DUR(j) + sum(k in JOBS) clean(k)
! One position for every job
all_different(rank)
! Solve the problem
if not cp_minimize(cycleTime) then
writeln("Problem is infeasible")
exit(1)
end-if
cp_show_stats
! Solution printing
writeln("Minimum cycle time: ", getsol(cycleTime))
writeln("Sequence of batches:\nBatch Duration Cleaning")
forall(k in JOBS)
writeln(formattext(" %d%8d%9d", getsol(rank(k)), DUR(getsol(rank(k))),
getsol(clean(k))))
end-model
Results
The minimum cycle time for this problem is 243 minutes which is achieved with the following sequence of batches: 1 → 4 → 3 → 5 → 2 → 1. This time includes 202 minutes of (incompressible) processing time and 41 minutes of cleaning.
When comparing the problem statistics produced by Xpress Kalis for this problem we see that the second model is a weaker formulation resulting in a considerably longer enumeration (using the default strategies).
equiv: Location of income tax offices
The example description in the following sections is taken from Section 15.5 `Location of income tax offices' of the book `Applications of optimization with Xpress-MP'.
The income tax administration is planning to restructure the network of income tax offices in a region. The number of inhabitants of every city and the distances between each pair of cities are known (Table Distance matrix and population of cities). The income tax administration has determined that offices should be established in three cities to provide sufficient coverage. Where should these offices be located to minimize the average distance per inhabitant to the closest income tax office?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 15 | 37 | 55 | 24 | 60 | 18 | 33 | 48 | 40 | 58 | 67 |
| 2 | 15 | 0 | 22 | 40 | 38 | 52 | 33 | 48 | 42 | 55 | 61 | 61 |
| 3 | 37 | 22 | 0 | 18 | 16 | 30 | 43 | 28 | 20 | 58 | 39 | 39 |
| 4 | 55 | 40 | 18 | 0 | 34 | 12 | 61 | 46 | 24 | 62 | 43 | 34 |
| 5 | 24 | 38 | 16 | 34 | 0 | 36 | 27 | 12 | 24 | 49 | 37 | 43 |
| 6 | 60 | 52 | 30 | 12 | 36 | 0 | 57 | 42 | 12 | 50 | 31 | 22 |
| 7 | 18 | 33 | 43 | 61 | 27 | 57 | 0 | 15 | 45 | 22 | 40 | 61 |
| 8 | 33 | 48 | 28 | 46 | 12 | 42 | 15 | 0 | 30 | 37 | 25 | 46 |
| 9 | 48 | 42 | 20 | 24 | 24 | 12 | 45 | 30 | 0 | 38 | 19 | 19 |
| 10 | 40 | 55 | 58 | 62 | 49 | 50 | 22 | 37 | 38 | 0 | 19 | 40 |
| 11 | 58 | 61 | 39 | 43 | 37 | 31 | 40 | 25 | 19 | 19 | 0 | 21 |
| 12 | 67 | 61 | 39 | 34 | 43 | 22 | 61 | 46 | 19 | 40 | 21 | 0 |
| Pop. (in 1000) | 15 | 10 | 12 | 18 | 5 | 24 | 11 | 16 | 13 | 22 | 19 | 20 |
Model formulation
Let CITIES be the set of cities. For the formulation of the problem, two groups of decision variables are necessary: a variable buildc that is one if and only if a tax office is established in city c, and a variable dependc that takes the number of the office on which city c depends. For the formulation of the constraints, we further introduce two sets of auxiliary variables: depdistc, the distance from city c to the office indicated by dependc, and numdepc, the number of cities depending on an office location.
The following relations are required to link the buildc with the dependc variables:
(1) numdepc counts the number of occurrences of office location c among the variables dependc.
(2) numdepc ≥ 1 if and only if the office in c is built (as a consequence, if the office in c is not built, then we must have numdepc = 0).
∀ c ∈ CITIES: numdepc ≥ 1 ⇔ buildc = 1
Since the number of offices built is limited by the given bound NUMLOC
| ∑ |
| c ∈ CITIES |
it would actually be sufficient to formulate the second relation between the buildc and dependc variables as the implication `If numdepc ≥ 1 then the office in c must be built, and inversely, if the office in c is not built, then we must have numdepc = 0'.
The objective function to be minimized is the total distance weighted by the number of inhabitants of the cities. We need to divide the resulting value by the total population of the region to obtain the average distance per inhabitant to the closest income tax office. The distance depdistc from city c to the closest tax office location is obtained by a discrete function, namely the row c of the distance matrix DISTcd indexed by the value of dependc:
We now obtain the following CP model:
| ∑ |
| c ∈ CITIES |
∀ c ∈ CITIES: buildc ∈ {0,1}, dependc ∈ CITIES,
numdepc ∈ CITIES ∪ {0}, depdistc ∈ {mind∈CITIESDISTc,d,..., maxd∈CITIESDISTc,d}
∀ c ∈ CITIES: depdistc = DISTc,dependc
| ∑ |
| c ∈ CITIES |
∀ c ∈ CITIES: numdepc = |dependd = c|d∈CITIES
∀ c ∈ CITIES: numdepc ≥ 1 ⇔ buildc = 1
Implementation
To solve this problem, we define a branching strategy with two parts, one for the buildc variables and a second strategy for the depdistc variables. The latter are enumerated using the split_domain branching scheme that divides the domain of the branching variable into several disjoint subsets (instead of assigning a value to the variable). We now pass an array of type cpbranching as the argument to procedure cp_set_branching. The different strategies will be applied in their order in this array. Since our enumeration strategy does not explicitly include all decision variables of the problem, Xpress Kalis will enumerate these using the default strategy if any unassigned variables remain after the application of our search strategy.
The objective function—a scalar product of an array of numerical coefficients and an array of decision variables—can be stated as a linear expression, but it will be computationally more efficient to employ the dedicated dot constraint to formulate this sum expression as shown in the example implementation.
model "J-5 Tax office location (CP)"
uses "kalis"
forward procedure calculate_dist
setparam("KALIS_DEFAULT_LB", 0)
declarations
NC = 12
CITIES = 1..NC ! Set of cities
DIST: array(CITIES,CITIES) of integer ! Distance matrix
POP: array(CITIES) of integer ! Population of cities
LEN: dynamic array(CITIES,CITIES) of integer ! Road lengths
NUMLOC: integer ! Desired number of tax offices
D: array(CITIES) of integer ! Auxiliary array used in constr. def.
build: array(CITIES) of cpvar ! 1 if office in city, 0 otherwise
depend: array(CITIES) of cpvar ! Office on which city depends
depdist: array(CITIES) of cpvar ! Distance to tax office
numdep: array(CITIES) of cpvar ! Number of depending cities per off.
totDist: cpvar ! Objective function variable
Strategy: array(1..2) of cpbranching ! Branching strategy
end-declarations
initializations from 'Data/j5tax.dat'
LEN POP NUMLOC
end-initializations
! Calculate the distance matrix
calculate_dist
forall(c in CITIES) do
build(c) <= 1
1 <= depend(c); depend(c) <= NC
min(d in CITIES) DIST(c,d) <= depdist(c)
depdist(c) <= max(d in CITIES) DIST(c,d)
numdep(c) <= NC
end-do
! Distance from cities to tax offices
forall(c in CITIES) do
forall(d in CITIES) D(d):=DIST(c,d)
element(D, depend(c)) = depdist(c)
end-do
! Number of cities depending on every office
forall(c in CITIES) occurrence(c, depend) = numdep(c)
! Relations between dependencies and offices built
forall(c in CITIES) equiv( build(c) = 1, numdep(c) >= 1 )
! Limit total number of offices
sum(c in CITIES) build(c) <= NUMLOC
! Branching strategy
Strategy(1):= assign_and_forbid(KALIS_MAX_DEGREE, KALIS_MAX_TO_MIN, build)
Strategy(2):= split_domain(KALIS_SMALLEST_DOMAIN, KALIS_MIN_TO_MAX,
depdist, true, 5)
cp_set_branching(Strategy)
! Objective: weighted total distance
! totDist = sum(c in CITIES) POP(c)*depdist(c)
! Equivalent formulation:
totDist = dot(POP,depdist)
! Solve the problem
if not cp_minimize(totDist) then
writeln("Problem is infeasible")
exit(1)
end-if
! Solution printing
writeln("Total weighted distance: ", getsol(totDist),
" (average per inhabitant: ",
getsol(totDist)/sum(c in CITIES) POP(c), ")")
forall(c in CITIES | getsol(build(c))>0) do
write("Office in ", c, ": ")
forall(d in CITIES | getsol(depend(d))=c) write(" ",d)
writeln
end-do
!-----------------------------------------------------------------
! Calculate the distance matrix using Floyd-Warshall algorithm
procedure calculate_dist
! Initialize all distance labels with a sufficiently large value
BIGM:=sum(c,d in CITIES | exists(LEN(c,d))) LEN(c,d)
forall(c,d in CITIES) DIST(c,d):=BIGM
forall(c in CITIES) DIST(c,c):=0 ! Set values on the diagonal to 0
! Length of existing road connections
forall(c,d in CITIES | exists(LEN(c,d))) do
DIST(c,d):=LEN(c,d)
DIST(d,c):=LEN(c,d)
end-do
! Update shortest distance for every node triple
forall(b,c,d in CITIES | c<d )
if DIST(c,d) > DIST(c,b)+DIST(b,d) then
DIST(c,d):= DIST(c,b)+DIST(b,d)
DIST(d,c):= DIST(c,b)+DIST(b,d)
end-if
end-procedure
end-model
This implementation contains another example of the use of a subroutine in Mosel: the calculation of the distance data is carried out in the procedure calculate_dist. We thus use a subroutine to structure our model, removing secondary tasks from the main model formulation.
Results
The optimal solution to this problem has a total weighted distance of 2438. Since the region has a total of 185,000 inhabitants, the average distance per inhabitant is 2438/185 ≈ 13.178 km. The three offices are established at nodes 1, 6, and 11. The first serves cities 1, 2, 5, 7, the office in node 6 cities 3, 4, 6, 9, and the office in node 11 cities 8, 10, 11, 12.
cycle: Paint production
In this section we work once more with the paint production problem from Section implies: Paint production. The objective of this problem is to determine a production cycle of minimal length for a given set of jobs with sequence-dependent cleaning times between every pair of jobs.
Model formulation
The problem formulation in Section implies: Paint production uses 'all-different' constraints to ensure that every job occurs once only, calculates the duration of cleaning times with 'element' constraints, and introduces auxiliary variables and constraints to prevent subcycles in the production sequence. All these constraints can be expressed by a single constraint relation, the 'cycle' constraint.
Let JOBS = {1,...,NJ} be the set of batches to produce, DURj the processing time for batch j, and CLEANij the cleaning time between the consecutive batches i and j. As before we define decision variables succj taking their values in JOBS, to indicate the successor of every job. The complete model formulation is the following,
| ∑ |
| j ∈ JOBS |
∀ j ∈ JOBS: succj ∈ JOBS \ {j}
cleantime = cycle((succj)j∈JOBS, (CLEANij)i,j∈JOBS)
where 'cycle' stands for the relation 'sequence into a single cycle without subcycles or repetitions'. The variable cleantime equals the total duration of the cycle.
Implementation
The Mosel model using the cycle constraint looks as follows.
model "B-5 Paint production (CP)"
uses "kalis", "mmsystem"
setparam("KALIS_DEFAULT_LB", 0)
declarations
NJ = 5 ! Number of paint batches (=jobs)
JOBS=0..NJ-1
DUR: array(JOBS) of integer ! Durations of jobs
CLEAN: array(JOBS,JOBS) of integer ! Cleaning times between jobs
succ: array(JOBS) of cpvar ! Successor of a batch
cleanTime,cycleTime: cpvar ! Durations of cleaning / complete cycle
end-declarations
initializations from 'Data/b5paint.dat'
DUR CLEAN
end-initializations
forall(j in JOBS) do
0 <= succ(j); succ(j) <= NJ-1; succ(j) <> j
end-do
! Assign values to 'succ' variables as to obtain a single cycle
! 'cleanTime' is the sum of the cleaning times
cycle(succ, cleanTime, CLEAN)
! Objective: minimize the duration of a production cycle
cycleTime = cleanTime +sum(j in JOBS) DUR(j)
! Solve the problem
if not cp_minimize(cycleTime) then
writeln("Problem is infeasible")
exit(1)
end-if
cp_show_stats
! Solution printing
writeln("Minimum cycle time: ", getsol(cycleTime))
writeln("Sequence of batches:\nBatch Duration Cleaning")
first:=1
repeat
writeln(formattext(" %d%8d%9d", first, DUR(first),
CLEAN(first,succ(first).sol)) )
first:=getsol(succ(first))
until (first=1)
end-model
Notice that we have renumbered the tasks, starting the index range with 0, to conform with the input format expected by the cycle constraint.
Results
The optimal solution to this problem has a minimum cycle time of 243 minutes, resulting from 202 minutes of (incompressible) processing time and 41 minutes of cleaning.
The problem statistics produced by Xpress Kalis for a model run reveal that the 'cycle' version of this model is the most efficient way of representing and solving the problem: it takes fewer nodes and a shorter execution time than the two versions of Section implies: Paint production.
Generic binary constraints: Euler knight tour
Our task is to find a tour on a chessboard for a knight figure such that the knight moves through every cell exactly once and at the end of the tour returns to its starting point. The path of the knight must follow the standard chess rules: a knight moves either one cell vertically and two cells horizontally, or two cells in the vertical and one cell in the horizontal direction, as shown in the following graphic (Figure Permissible moves for a knight):
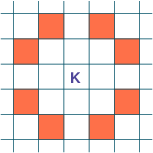
Figure 3.3: Permissible moves for a knight
Model formulation
To represent the chessboard we number the cells from 0 to N-1, where N is the number of cells of the board. The path of the knight is defined by N variables posi that indicate the ith position of the knight on its tour.
The first variable is fixed to zero as the start of the tour. Another obvious constraint we need to state is that all variables posi take different values (every cell of the chessboard is visited exactly once):
We are now left with the necessity to establish a constraint relation that checks whether consecutive positions define a valid knight move. To this aim we define a new binary constraint 'valid_knight_move' that checks whether a given pair of values defines a permissible move according to the chess rules for knight moves. Vertically and horizontally, the two values must be no more than two cells apart and the sum of the vertical and horizontal difference must be equal to three. The complete model then looks as follows.
pos1 = 0
all-different(pos1,...,posN)
∀i ∈ POS={1,...,N-1}: valid_knight_move(posi,posi+1)
valid_knight_move(posN,pos1)
Implementation
Testing whether moving from position a to position b is a valid move for a knight figure can be done with the following function valid_knight_move where 'div' means integer division without rest and 'mod' is the rest of the integer division:
| function valid_knight_move(a,b) xa := a div E ya := a mod E xb := b div E yb := b mod E deltax := |xa-xb| deltay := |ya-yb| return ((deltax ≤ 2) and (deltay ≤ 2) and (deltax + deltay = 3)) end-function |
The following Mosel model defines the user constraint function valid_knight_move as the implementation of the new binary constraints on pairs of movep variables (the constraints are established with generic_binary_constraint).
model "Euler Knight Moves"
uses "kalis"
parameters
S = 8 ! Number of rows/columns
NBSOL = 1 ! Number of solutions sought
end-parameters
forward procedure print_solution(sol: integer)
forward public function valid_knight_move(a:integer, b:integer): boolean
N:= S * S ! Total number of cells
setparam("KALIS_DEFAULT_LB", 0)
setparam("KALIS_DEFAULT_UB", N-1)
declarations
PATH = 1..N ! Cells on the chessboard
pos: array(PATH) of cpvar ! Cell at position p in the tour
end-declarations
! Fix the start position
pos(1) = 0
! Each cell is visited once
all_different(pos, KALIS_GEN_ARC_CONSISTENCY)
! The path of the knight obeys the chess rules for valid knight moves
forall(i in 1..N-1)
generic_binary_constraint(pos(i), pos(i+1), "valid_knight_move")
generic_binary_constraint(pos(N), pos(1), "valid_knight_move")
! Setting enumeration parameters
cp_set_branching(probe_assign_var(KALIS_SMALLEST_MIN, KALIS_MAX_TO_MIN,
pos, 14))
! Search for up to NBSOL solutions
solct:= 0
while (solct<NBSOL and cp_find_next_sol) do
solct+=1
cp_show_stats
print_solution(solct)
end-do
! **** Test whether the move from position a to b is admissible ****
public function valid_knight_move(a:integer, b:integer): boolean
declarations
xa,ya,xb,yb,delta_x,delta_y: integer
end-declarations
xa := a div S
ya := a mod S
xb := b div S
yb := b mod S
delta_x := abs(xa-xb)
delta_y := abs(ya-yb)
returned := (delta_x<=2) and (delta_y<=2) and (delta_x+delta_y=3)
end-function
!****************************************************************
! Solution printing
procedure print_solution(sol: integer)
writeln("Solution ", sol, ":")
forall(i in PATH)
write(getval(pos(i)), if(i mod 10 = 0, "\n ", ""), " -> ")
writeln("0")
end-procedure
end-model
The branching scheme used in this model is the probe_assign_var heuristic, in combination with the variable selection KALIS_SMALLEST_MIN (choose variable with smallest lower bound) and the value selection criterion KALIS_MAX_TO_MIN (from largest to smallest domain value). Another search strategy that was found to work well (though slower than the strategy in the code listing) is
cp_set_branching(assign_var(KALIS_SMALLEST_MIN, KALIS_MAX_TO_MIN, pos))
Our model defines two parameters. It is thus possible to change either the size of the chessboard (S) or the number of solutions sought (NBSOL) when executing the model without having to modify the model source.
Results
The first solution printed out by our model is the following tour.
0 -> 17 -> 34 -> 51 -> 36 -> 30 -> 47 -> 62 -> 45 -> 39 -> 54 -> 60 -> 43 -> 33 -> 48 -> 58 -> 52 -> 35 -> 41 -> 56 -> 50 -> 44 -> 38 -> 55 -> 61 -> 46 -> 63 -> 53 -> 59 -> 49 -> 32 -> 42 -> 57 -> 40 -> 25 -> 8 -> 2 -> 19 -> 4 -> 14 -> 31 -> 37 -> 22 -> 7 -> 13 -> 28 -> 18 -> 24 -> 9 -> 3 -> 20 -> 26 -> 16 -> 1 -> 11 -> 5 -> 15 -> 21 -> 6 -> 23 -> 29 -> 12 -> 27 -> 10 -> 0
Alternative implementation
Whereas the aim of the model above is to give an example of the definition of user constraints, it is possible to implement this problem in a more efficient way using the model developed for the cyclic scheduling problem in Section cycle: Paint production. The set of successors (domains of variables succp) can be calculated using the same algorithm that we have used above in the implementation of the user-defined binary constraints.
Without repeating the complete model definition at this place, we simply display the model formulation, including the calculation of the sets of possible successors (procedure calculate_successors, and the modified procedure print_sol for solution printout. We use a simpler version of the 'cycle' constraints than the one we have seen in Section cycle: Paint production, its only argument is the set of successor variables—there are no weights to the arcs in this problem.
model "Euler Knight Moves"
uses "kalis"
parameters
S = 8 ! Number of rows/columns
NBSOL = 1 ! Number of solutions sought
end-parameters
forward procedure calculate_successors(p: integer)
forward procedure print_solution(sol: integer)
N:= S * S ! Total number of cells
setparam("KALIS_DEFAULT_LB", 0)
setparam("KALIS_DEFAULT_UB", N)
declarations
PATH = 0..N-1 ! Cells on the chessboard
succ: array(PATH) of cpvar ! Successor of cell p
end-declarations
! Calculate set of possible successors
forall(p in PATH) calculate_successors(p)
! Each cell is visited once, no subtours
cycle(succ)
! Search for up to NBSOL solutions
solct:= 0
while (solct<NBSOL and cp_find_next_sol) do
solct+=1
cp_show_stats
print_solution(solct)
end-do
! **** Calculate possible successors ****
procedure calculate_successors(p: integer)
declarations
SuccSet: set of integer ! Set of successors
end-declarations
xp := p div S
yp := p mod S
forall(q in PATH) do
xq := q div S
yq := q mod S
delta_x := abs(xp-xq)
delta_y := abs(yp-yq)
if (delta_x<=2) and (delta_y<=2) and (delta_x+delta_y=3) then
SuccSet +={q}
end-if
end-do
setdomain(succ(p), SuccSet)
end-procedure
!****************************************************************
! **** Solution printing ****
procedure print_solution(sol: integer)
writeln("Solution ", sol, ":")
thispos:=0
nextpos:=getval(succ(0))
ct:=1
while (nextpos<>0) do
write(thispos, if(ct mod 10 = 0, "\n ", ""), " -> ")
val:=getval(succ(thispos))
thispos:=nextpos
nextpos:=getval(succ(thispos))
ct+=1
end-do
writeln("0")
end-procedure
end-model
The calculation of the domains for the succp variables reduces these to 2-8 elements (as compared to the N=64 values for every posp variables), which clearly reduces the search space for this problem.
This second model finds the first solution to the problem after 131 nodes taking just a fraction of a second to execute on a standard PC whereas the first model requires several thousand nodes and considerably longer running times. It is possible to reduce the number of branch-and-bound nodes even further by using yet another version of the 'cycle' constraint that works with successor and predecessor variables. This version of 'cycle' performs a larger amount of propagation, at the expense of (slightly) slower execution times for our problem. The procedure calculate_successors now sets the domain of predp to the same values as succp for all cells p.
declarations PATH = 0..N-1 ! Cells on the chessboard succ: array(PATH) of cpvar ! Successor of cell p pred: array(PATH) of cpvar ! Predecessor of cell p end-declarations ! Calculate sets of possible successors and predecessors forall(p in PATH) calculate_successors(p) ! Each cell is visited once, no subtours cycle(succ, pred)
Figure Knight's tour solution graph shows the graphical display of a knight's tour created with the user graph drawing functionality.
Figure 3.4: Knight's tour solution graph
Alternative implementation 2
Yet more efficient (a similar number of nodes with significantly shorter running times) is the following model version using the 'cycle' constraint described in Section cycle: Paint production. Since travel times from one position to the next are irrelevant in this model we simply fix all coefficients for the 'cycle' constraint to a constant and constrain the cycle length to the corresponding value.
All else, including the calculation of the sets of possible successors (procedure calculate_successors, and the procedure print_sol for solution printout is copied unchanged from the previous model.
model "Euler Knight Moves"
uses "kalis"
parameters
S = 8 ! Number of rows/columns
NBSOL = 1 ! Number of solutions sought
end-parameters
forward procedure calculate_successors(p: integer)
forward procedure print_solution(sol: integer)
N:= S * S ! Total number of cells
setparam("KALIS_DEFAULT_LB", 0)
setparam("KALIS_DEFAULT_UB", N)
declarations
PATH = 0..N-1 ! Cells on the chessboard
succ: array(PATH) of cpvar ! Successor of cell p
end-declarations
! Calculate set of possible successors
forall(p in PATH) calculate_successors(p)
! Each cell is visited once, no subtours
cycle(succ)
! Search for up to NBSOL solutions
solct:= 0
while (solct<NBSOL and cp_find_next_sol) do
solct+=1
cp_show_stats
print_solution(solct)
end-do
! **** Calculate possible successors ****
procedure calculate_successors(p: integer)
declarations
SuccSet: set of integer ! Set of successors
end-declarations
xp := p div S
yp := p mod S
forall(q in PATH) do
xq := q div S
yq := q mod S
delta_x := abs(xp-xq)
delta_y := abs(yp-yq)
if (delta_x<=2) and (delta_y<=2) and (delta_x+delta_y=3) then
SuccSet +={q}
end-if
end-do
setdomain(succ(p), SuccSet)
end-procedure
!****************************************************************
! **** Solution printing ****
procedure print_solution(sol: integer)
writeln("Solution ", sol, ":")
thispos:=0
nextpos:=getval(succ(0))
ct:=1
while (nextpos<>0) do
write(thispos, if(ct mod 10 = 0, "\n ", ""), " -> ")
val:=getval(succ(thispos))
thispos:=nextpos
nextpos:=getval(succ(thispos))
ct+=1
end-do
writeln("0")
end-procedure
end-model
Symmetry breaking: scenes allocation problem
A movie producer has to decide when to shoot the scenes for a movie. Every scene involves a specific set of actors. A least 2 scenes and at most 5 scenes can be filmed per day. All actors of a scene must, of course, be present on the day the scene is shot. The actors have fees representing the amount they are paid per day they spend in the studio. The movie producer wishes to minimize the production costs incurred through the actors' fees.
Model formulation
Let SCENES denote the set of scenes, ACTORS all the actors taking part in the movie, and DAYS the set of eligible days. The decision variables shoots indicating which day a scene is shot take their values in the set DAYS. A second set of variables are the binary indicators workad that take the value 1 if actor a works on the day d.
Every day, the number of scenes shot needs to lie within the interval of minimum and maximum permissible numbers (MINSCENESHOTd,...,MAXSCENESHOTd). We also need to formulate the implication 'if an actor works on a day, then this day is due', or stated otherwise 'if a scene that the actor appears in is scheduled on day d, then the actor is working on this day':
∀ a ∈ ACTORS, d ∈ DAYS: workad ∈ {0,1}
∀ d ∈DAYS: |shoots = d|s ∈ SCENES ∈ {MINSCENESHOTd,...,MAXSCENESHOTd}
∀ a ∈ ACTORS, s ∈ APPEARa, d ∈ DAYS: shoots=d ⇒ workad=1
The objective function is to minimize the total cost incurred through actors' fees:
Symmetry breaking constraints: it is easy to see that days are entirely interchangeable (e.g. all scenes from day 1 could be exchanged with those assigned to day 2 without any impact on the total cost). Indeed, any permuation of days with the same scene allocations will result in the same total cost. So it might be worthwhile to investigate how we can reduce the number of permutations in order to shorten solving times.
Consider a scene s1: it needs to be assigned some specific day, say day 1 (all days are interchangeable at this point). Now consider a second scene s2: it can either be assigned the same day as the first or some other (additional) day—all other days being interchangeable at this point we can assume this will be day 2. Generalizing this observation, for any scene s we can limit its value set to the days already used by scenes 1,...,s-1 plus one additional day, that is:
∀ s ∈SCENES, s>1: shoots ≤ maximum(shoot1,...,shoots-1) + 1
Implementation
For the implementation of the lower and upper bounds on the number of scenes to be shot per day we use a global cardinality ('distribute') constraint that distributes the scenes to be shot over the available days.
For the formulation of the symmetry breaking constraints some auxiliary objects are introduced, namely the list shootListSb of the predecessors of scene s (that is, shoot1,...,shoots-1) in enumeration order of the set of scenes, and an additional decision variable maxShootSbs defined as the maximum value among the variables in this list.
model "Scenes Allocation (CP)"
uses "kalis" ! Gain access to the Xpress Kalis solver
! **** Data ****
declarations
SCENES: range ! Set of scene numbers
DAYS = 1..5 ! Day numbers when the scenes can be shot
ACTORS: set of string ! Set of actors
DAILYFEE: array(ACTORS) of integer ! Daily fees of actors
CAST: array(SCENES) of set of string ! Cast of actors per scene
APPEAR: array(ACTORS) of set of integer ! Scenes where an actor appears
MINSCENESHOT: array(DAYS) of integer ! Minimum number of scenes per day
MAXSCENESHOT: array(DAYS) of integer ! Maximum number of scenes per day
end-declarations
! Initialize actors DAILYFEE
DAILYFEE::(["Georges Clooney","Penelope Cruz","Leonardo DiCaprio",
"Nathalie Portman","Ryan Gosling","Monica Bellucci","Javier Bardem",
"Keira Knightley","Vincent Cassel","Marion Cotillard","Emma Watson"])[264, 250, 303,
40, 75, 93, 87, 57, 74, 33, 95]
! Initialize minimum and maximum numbers of scenes that have to be shot per day
MINSCENESHOT::([1,2,3,4,5])[2,2,2,2,2]
MAXSCENESHOT::([1,2,3,4,5])[5,5,5,5,5]
! Initialize sets of actors per scene
CAST(1):= {"Monica Bellucci"}
CAST(2):= {"Georges Clooney","Monica Bellucci","Ryan Gosling","Nathalie Portman"}
CAST(3):= {"Keira Knightley","Leonardo DiCaprio","Vincent Cassel","Ryan Gosling"}
CAST(4):= {"Penelope Cruz","Vincent Cassel"}
CAST(5):= {"Vincent Cassel","Javier Bardem","Georges Clooney","Keira Knightley","Marion Cotillard"}
CAST(6):= {"Emma Watson","Keira Knightley","Javier Bardem","Leonardo DiCaprio","Marion Cotillard"}
CAST(7):= {"Penelope Cruz","Georges Clooney"}
CAST(8):= {"Vincent Cassel","Nathalie Portman"}
CAST(9):= {"Penelope Cruz","Keira Knightley","Vincent Cassel","Leonardo DiCaprio","Emma Watson"}
CAST(10):= {"Penelope Cruz","Keira Knightley","Leonardo DiCaprio","Georges Clooney"}
CAST(11):= {"Georges Clooney"}
CAST(12):= {"Monica Bellucci","Emma Watson","Keira Knightley","Nathalie Portman","Ryan Gosling"}
CAST(13):= {"Monica Bellucci","Nathalie Portman","Penelope Cruz","Georges Clooney"}
CAST(14):= {"Javier Bardem","Leonardo DiCaprio"}
CAST(15):= {"Emma Watson","Nathalie Portman","Keira Knightley","Georges Clooney"}
CAST(16):= {"Leonardo DiCaprio","Keira Knightley","Penelope Cruz","Vincent Cassel"}
CAST(17):= {"Leonardo DiCaprio","Georges Clooney","Ryan Gosling"}
CAST(18):= {"Leonardo DiCaprio","Keira Knightley","Monica Bellucci","Emma Watson"}
CAST(19):= {"Penelope Cruz"}
! Calculate appearance in scenes for each actor
forall(a in ACTORS) APPEAR(a):= union(s in SCENES | a in CAST(s)) {s}
! **** Problem statement ****
declarations
shoot: array(SCENES) of cpvar ! Decision var.s: day when a scene will be shot
work: array(ACTORS,DAYS) of cpvar
! Decision var.s: presence of actor i on day k
totalCost: cpvar ! Objective
shootListSb: cpvarlist ! List of shoot variables for symmetry breaking
maxShootSb: array(SCENES) of cpvar ! Max. value of shoot variables list
! per scene (formulation of symmetry breaking)
end-declarations
setparam("kalis_default_ub", 200000000) ! Kalis default upper bound
! **** Domain definition ****
! Each shoot variable takes a value from the set DAYS
forall(s in SCENES) do
setname(shoot(s),"shoot["+s+"]")
setdomain(shoot(s), DAYS)
end-do
! The total cost has a lower bound of $0 and an upper bound of $200000000
setname(totalCost, "totalCost")
setdomain(totalCost, 0, 200000000)
! work : binary variables that indicate if actor i is present on day k
forall(a in ACTORS, d in DAYS) do
setname(work(a,d), "work["+a+","+d+"]")
setdomain(work(a,d), 0, 1)
end-do
! **** Constraints ****
! Global Cardinality Constraint to express lower and upper bounds on the
! number of scenes that have to be shot each day
distribute(shoot,DAYS,MINSCENESHOT,MAXSCENESHOT)
! When an actor works on a day, this day is due
forall(a in ACTORS, s in APPEAR(a), d in DAYS)
implies(shoot(s)=d, work(a,d)=1)
! Symmetry breaking
shoot(1) = 1 ! All days are interchangeable at this stage
forall(s in SCENES | s > 1) do
shootListSb += shoot(s-1) ! For a scene s, we need to consider
maxShootSb(s) = maximum(shootListSb) ! just the previously used days + 1:
shoot(s) <= maxShootSb(s)+1 ! D(s)={1,...,max(shoot(1),...,shoot(s-1))+1}
end-do
! Objective function
totalCost = sum(a in ACTORS, d in DAYS) DAILYFEE(a)*work(a,d)
! Branching strategy
cp_set_branching(assign_and_forbid(KALIS_INPUT_ORDER, KALIS_MIN_TO_MAX, shoot))
! **** Problem solving and solution reporting ****
if cp_minimize(totalCost) then
! Display total cost
writeln("Total cost: ", getsol(totalCost))
! Display scenes scheduled on each day
forall(d in DAYS) do
write("\nDay ", d, ": scenes ")
forall(s in SCENES | getsol(shoot(s))=d) write(s, " ")
end-do
! Display days worked by each actor
forall(a in ACTORS) do
write("\n", strfmt(a,-16), " :")
forall(d in DAYS | getsol(work(a,d)) = 1) write(" Day ",d)
end-do
writeln
else
writeln("No solution found.")
end-if
end-model
Results
The model shown above generates the following output:
Total cost: 3497 Day 1: scenes 1 8 Day 2: scenes 2 5 11 12 15 Day 3: scenes 3 7 10 13 17 Day 4: scenes 4 19 Day 5: scenes 6 9 14 16 18 Georges Clooney : Day 2 Day 3 Penelope Cruz : Day 3 Day 4 Day 5 Leonardo DiCaprio: Day 3 Day 5 Nathalie Portman : Day 1 Day 2 Day 3 Ryan Gosling : Day 2 Day 3 Monica Bellucci : Day 1 Day 2 Day 3 Day 5 Javier Bardem : Day 2 Day 5 Keira Knightley : Day 2 Day 3 Day 5 Vincent Cassel : Day 1 Day 2 Day 3 Day 4 Day 5 Marion Cotillard : Day 2 Day 5 Emma Watson : Day 2 Day 5
Without the symmetry breaking constraints, the solving time is more than one order of magnitude longer (both for finding the optimal solution and proving its optimality) than when these constraints are included in the model.
© 2001-2025 Fair Isaac Corporation. All rights reserved. This documentation is the property of Fair Isaac Corporation (“FICO”). Receipt or possession of this documentation does not convey rights to disclose, reproduce, make derivative works, use, or allow others to use it except solely for internal evaluation purposes to determine whether to purchase a license to the software described in this documentation, or as otherwise set forth in a written software license agreement between you and FICO (or a FICO affiliate). Use of this documentation and the software described in it must conform strictly to the foregoing permitted uses, and no other use is permitted.

